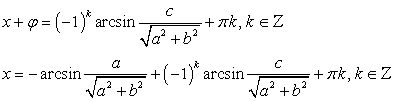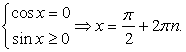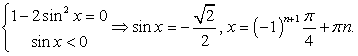Комбинированные уравнения
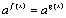 , откуда следует, что
, откуда следует, что 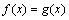 . Иногда такое преобразование можно провести непосредственно, в других случаях требуется предварительно сделать замену переменной.Пример 1. Решить уравнение:
. Иногда такое преобразование можно провести непосредственно, в других случаях требуется предварительно сделать замену переменной.Пример 1. Решить уравнение: 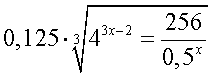 .Решение.Представим обе части равенства в виде степеней с основанием 2:
.Решение.Представим обе части равенства в виде степеней с основанием 2: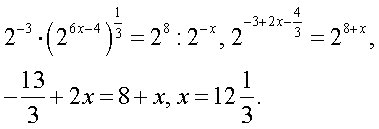 Ответ:
Ответ: 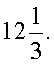 Пример 2. Решить уравнение: 4x+2 + 2 ∙
4x – 5x+2 = 5 ∙
5x.Решение.Поменяем порядок слагаемых:4x+2 + 2 ∙
4x = 5x+2 + 5 ∙
5x, 4x (16 + 2) = 5x (25+5),18 ∙
4x = 30 ∙
5x,
Пример 2. Решить уравнение: 4x+2 + 2 ∙
4x – 5x+2 = 5 ∙
5x.Решение.Поменяем порядок слагаемых:4x+2 + 2 ∙
4x = 5x+2 + 5 ∙
5x, 4x (16 + 2) = 5x (25+5),18 ∙
4x = 30 ∙
5x, 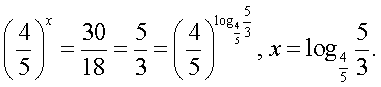 Ответ:
Ответ: 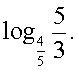 Пример 3. Решить уравнение: 2х+4 ∙
3х = 576.Решение.Преобразуем левую часть: 16 ∙
(2х ∙
3х) = 576 и разделим обе части на 16: 6х = 36, х = 2.Ответ: 2.Пример 4.Решить уравнение:
Пример 3. Решить уравнение: 2х+4 ∙
3х = 576.Решение.Преобразуем левую часть: 16 ∙
(2х ∙
3х) = 576 и разделим обе части на 16: 6х = 36, х = 2.Ответ: 2.Пример 4.Решить уравнение: 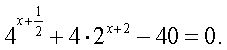 Решение.Запишем уравнение в виде:
Решение.Запишем уравнение в виде: 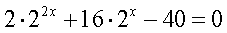 и сделаем замену: t = 2x (t >
0). Тогда:2t2 + 16t – 40 = 0,t2 + 8t – 20 = 0,t1 = 2, t2 = - 10 <
0 — посторонний корень.Обратная замена: 2х = 2, х = 1.Ответ: 1.Пример 5. Решить уравнение:
и сделаем замену: t = 2x (t >
0). Тогда:2t2 + 16t – 40 = 0,t2 + 8t – 20 = 0,t1 = 2, t2 = - 10 <
0 — посторонний корень.Обратная замена: 2х = 2, х = 1.Ответ: 1.Пример 5. Решить уравнение: 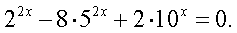 Решение.Если записать левую часть так:
Решение.Если записать левую часть так: 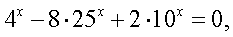 то можно заметить, что основания степеней (числа 4, 10, 25) образуют геометрическую прогрессию. В этом случае можно разделить обе части равенства, например, на 25х ( поскольку ни при каком х это выражение не равно нулю) и получить уравнение
то можно заметить, что основания степеней (числа 4, 10, 25) образуют геометрическую прогрессию. В этом случае можно разделить обе части равенства, например, на 25х ( поскольку ни при каком х это выражение не равно нулю) и получить уравнение 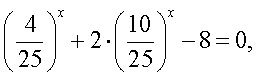 или
или 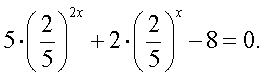 Замена
Замена 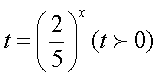 приводит к уравнению t2 + 2t – 8 = 0, t1 = 2, t2 = -4 <
0 — посторонний корень. Следовательно,
приводит к уравнению t2 + 2t – 8 = 0, t1 = 2, t2 = -4 <
0 — посторонний корень. Следовательно, 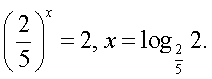 Ответ:
Ответ: 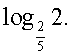 Пример 6. Решить уравнение: 12x ∙
4x – 5x ∙
2x + 1 – 9 ∙
4x + 1 + 30 ∙
2x = 0.Решение.Разложим левую часть на множители:
Пример 6. Решить уравнение: 12x ∙
4x – 5x ∙
2x + 1 – 9 ∙
4x + 1 + 30 ∙
2x = 0.Решение.Разложим левую часть на множители: 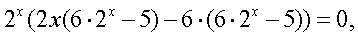 ,
, 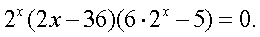 Первый множитель никогда не равен нулю, поэтому ответом будут корни уравнений:Ответ: 3;
Первый множитель никогда не равен нулю, поэтому ответом будут корни уравнений:Ответ: 3; 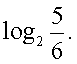 .Пример 7. Решить уравнение:
.Пример 7. Решить уравнение: 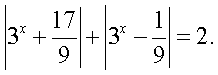 Решение.Заметим, что первое подмодульное выражение положительно при любом х, то есть его модуль равен подмодульному выражению. Рассмотрим две возможности для знака второго подмодульного выражения:
Решение.Заметим, что первое подмодульное выражение положительно при любом х, то есть его модуль равен подмодульному выражению. Рассмотрим две возможности для знака второго подмодульного выражения:- 1 случай.
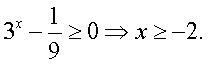 Тогда
Тогда 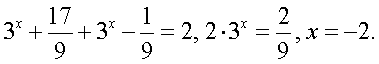 2 случай.
2 случай. 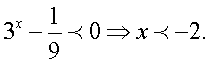 При этом
При этом 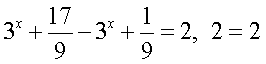 — тождество, следовательно, любое значение x <
-2 является решением уравнения.
— тождество, следовательно, любое значение x <
-2 является решением уравнения.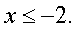 Пример 8.Решить уравнение:
Пример 8.Решить уравнение: 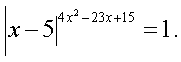 Решение.При решении этого уравнения важно не забыть, что равенство будет верным не только в случае, когда показатель степени равен 0, но и тогда, когда основание степени в левой части равно 1, так как при возведении 1 в любую степень мы получим 1. Кроме того, ОДЗ определяется условием: х – 5 ≠
0, то есть х ≠
5.1 случай.
Решение.При решении этого уравнения важно не забыть, что равенство будет верным не только в случае, когда показатель степени равен 0, но и тогда, когда основание степени в левой части равно 1, так как при возведении 1 в любую степень мы получим 1. Кроме того, ОДЗ определяется условием: х – 5 ≠
0, то есть х ≠
5.1 случай. 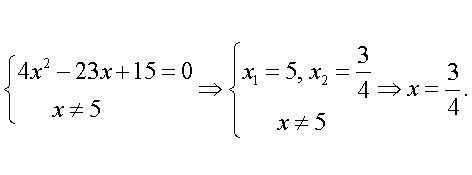 2 случай.
2 случай. 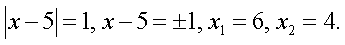 Ответ: 4; 6;
Ответ: 4; 6; 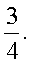 При решении логарифмических уравнений
При решении логарифмических уравнений , так же, как в случае иррациональных уравнений
, так же, как в случае иррациональных уравнений , возможно появление посторонних корней
, возможно появление посторонних корней . Причина их появления — – расширение области определения исходного уравнения. Поэтому и проверка корней логарифмического уравнения осуществляется либо непосредственно по предварительно найденной области определения, либо по условиям её задающим (подстановкой в соответствующую систему неравенств). Заметим, что иногда удобно осуществить проверку и непосредственной подстановкой найденных корней в исходное логарифмическое уравнение. Это, конечно же, допустимо. Естественно, что при решении логарифмических уравнений возможно и следование стратегии равносильных преобразований. Далее мы рассмотрим примеры решения разного рода.Расширение области определения при решении логарифмических уравнений связано, как правило, с двумя обстоятельствами:
. Причина их появления — – расширение области определения исходного уравнения. Поэтому и проверка корней логарифмического уравнения осуществляется либо непосредственно по предварительно найденной области определения, либо по условиям её задающим (подстановкой в соответствующую систему неравенств). Заметим, что иногда удобно осуществить проверку и непосредственной подстановкой найденных корней в исходное логарифмическое уравнение. Это, конечно же, допустимо. Естественно, что при решении логарифмических уравнений возможно и следование стратегии равносильных преобразований. Далее мы рассмотрим примеры решения разного рода.Расширение области определения при решении логарифмических уравнений связано, как правило, с двумя обстоятельствами:- а) преобразование потенцирования
 («отбрасывания» логарифмов, замена уравнения
(«отбрасывания» логарифмов, замена уравнения 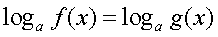 уравнением
уравнением 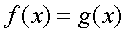 );б) использование «справа налево» формул:
);б) использование «справа налево» формул:
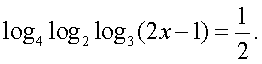 Решение.Будем представлять правую часть уравнения последовательно в виде логарифмов с основаниями 4, 2 и 3 и проводить преобразование потенцирования:
Решение.Будем представлять правую часть уравнения последовательно в виде логарифмов с основаниями 4, 2 и 3 и проводить преобразование потенцирования: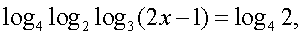
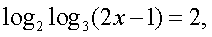
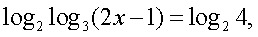
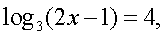
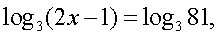
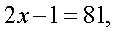 ,
, 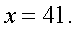 Проверим найденное значение непосредственной подстановкой в исходное уравнение:
Проверим найденное значение непосредственной подстановкой в исходное уравнение: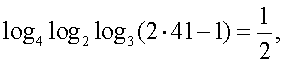
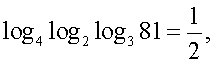
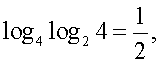
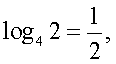
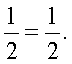 Мы пришли к верному числовому равенству. Таким образом,
Мы пришли к верному числовому равенству. Таким образом, 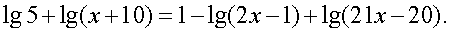 — единственный корень данного уравнения.Ответ: 41.Пример 10. Решим уравнение:
— единственный корень данного уравнения.Ответ: 41.Пример 10. Решим уравнение: 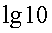 Решение.Представим 1 как
Решение.Представим 1 как 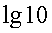 и преобразуем левую и правую части уравнения, исходя из свойств логарифмов:
и преобразуем левую и правую части уравнения, исходя из свойств логарифмов: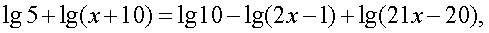
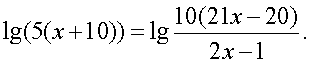 Потенцируя уравнение, получаем:
Потенцируя уравнение, получаем: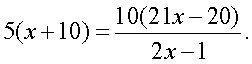 Решим это рациональное уравнение:
Решим это рациональное уравнение: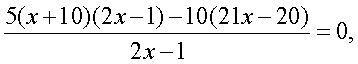
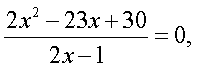
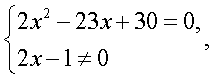
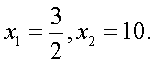 Осуществим проверку корней. Область определения исходного уравнения задается условиями:
Осуществим проверку корней. Область определения исходного уравнения задается условиями: 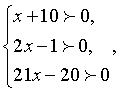 т.е. область определения:
т.е. область определения: 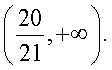 Оба корня, очевидно, принадлежат области определения. Таким образом, корни данного уравнения
Оба корня, очевидно, принадлежат области определения. Таким образом, корни данного уравнения  Ответ: 1,5; 10.Пример 11. Решим уравнение:
Ответ: 1,5; 10.Пример 11. Решим уравнение: 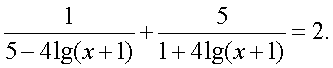 Решение.Пусть
Решение.Пусть 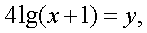 тогда получаем систему уравнений:
тогда получаем систему уравнений: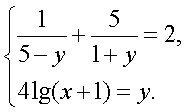 Корни первого уравнения системы:
Корни первого уравнения системы: 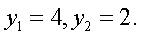 Тогда исходное уравнение равносильно совокупности:
Тогда исходное уравнение равносильно совокупности: 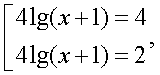 т.е.
т.е. 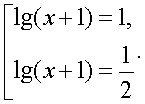 Потенцируя полученные уравнения приходим к выводу, что х = 9 или х =
Потенцируя полученные уравнения приходим к выводу, что х = 9 или х = 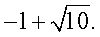 Оба этих значения являются корнями данного уравнения, поскольку его область определения задается условием х + 1 >
0, т.е. х >
-1.Ответ: 9;
Оба этих значения являются корнями данного уравнения, поскольку его область определения задается условием х + 1 >
0, т.е. х >
-1.Ответ: 9; 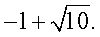 Если в уравнении содержатся логарифмы с разными основаниями, то следует привести их к одному основанию, воспользовавшись формулами перехода к новому основанию логарифма:Пример 12. Решим уравнение:
Если в уравнении содержатся логарифмы с разными основаниями, то следует привести их к одному основанию, воспользовавшись формулами перехода к новому основанию логарифма:Пример 12. Решим уравнение: 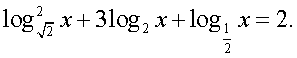 Решение.В данном уравнении перейдем к логарифмам по основанию 2:
Решение.В данном уравнении перейдем к логарифмам по основанию 2: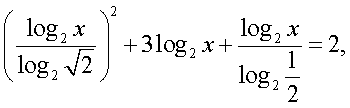
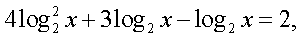
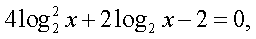
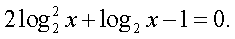 Последнее уравнение равносильно системе:
Последнее уравнение равносильно системе: 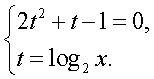 Корни первого уравнения системы
Корни первого уравнения системы 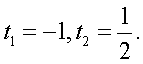 Таким образом, имеем совокупность уравнений:
Таким образом, имеем совокупность уравнений: 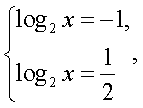 которая равносильна системе
которая равносильна системе 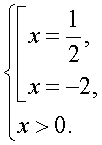 Откуда очевидно, что
Откуда очевидно, что 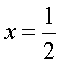 — единственный корень данного уравнения.Заметим, что применение формул перехода к новому основанию логарифма, как правило, приводит к изменению области определения уравнения. Поэтому следует анализировать в ходе решения, как возможность появления посторонних корней, так и возможность потери корней.Ответ: 0,5.Пример 13. Решим уравнение:
— единственный корень данного уравнения.Заметим, что применение формул перехода к новому основанию логарифма, как правило, приводит к изменению области определения уравнения. Поэтому следует анализировать в ходе решения, как возможность появления посторонних корней, так и возможность потери корней.Ответ: 0,5.Пример 13. Решим уравнение: 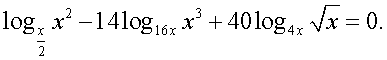 Решение.Прежде всего, воспользуемся известным свойством логарифма и получим одинаковое для всех логарифмов логарифмируемое выражение:
Решение.Прежде всего, воспользуемся известным свойством логарифма и получим одинаковое для всех логарифмов логарифмируемое выражение: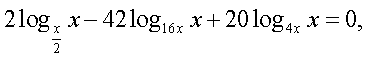
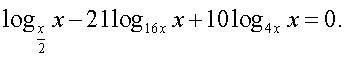 Теперь воспользуемся формулой перехода к новому основанию логарифма, получаем:
Теперь воспользуемся формулой перехода к новому основанию логарифма, получаем: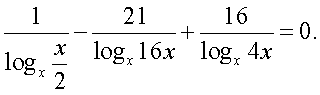 Далее имеем:
Далее имеем: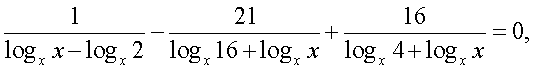
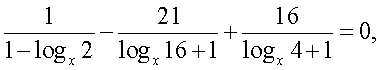
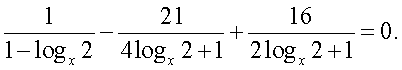 Корни второго уравнения системы:
Корни второго уравнения системы: 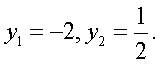 Следовательно, решение исходного уравнения свелось к решению совокупности:
Следовательно, решение исходного уравнения свелось к решению совокупности: 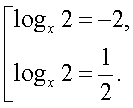 Решим первое уравнение совокупности:
Решим первое уравнение совокупности: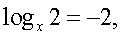
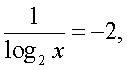
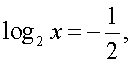
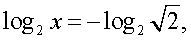
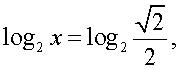
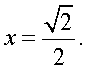 Аналогично, решая второе уравнение совокупности, получаем х = 4.Найдем, теперь область определения исходного уравнения и проведем проверку корней:
Аналогично, решая второе уравнение совокупности, получаем х = 4.Найдем, теперь область определения исходного уравнения и проведем проверку корней: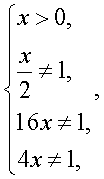 т.е.
т.е. 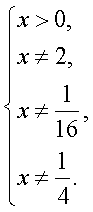 Ясно, что оба найденных значения х удовлетворяют области определения.Наконец, следует проанализировать возможную потерю корней. Для этого выясним, когда наши преобразования приводили к сужению области определения уравнения. После перехода к новому основанию логарифма дальнейшее решение осуществляется при условии:
Ясно, что оба найденных значения х удовлетворяют области определения.Наконец, следует проанализировать возможную потерю корней. Для этого выясним, когда наши преобразования приводили к сужению области определения уравнения. После перехода к новому основанию логарифма дальнейшее решение осуществляется при условии: 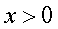 и
и 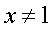 Дополнительное условие
Дополнительное условие 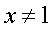 не имеет отношения к исходному уравнению, поэтому х = 1 — возможный потерянный корень. Подставив значение х = 1 в исходное уравнение, убеждаемся, что это действительно корень. Таким образом, корни исходного уравнения:
не имеет отношения к исходному уравнению, поэтому х = 1 — возможный потерянный корень. Подставив значение х = 1 в исходное уравнение, убеждаемся, что это действительно корень. Таким образом, корни исходного уравнения: 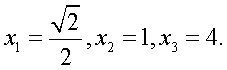 Ответ:
Ответ: 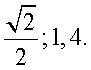 .Применяя при решении логарифмических уравнений формулы перехода к новому основанию целесообразней переходить к новому основанию не являющемуся выражением с переменной, а равному некоторому числу. Как правило, это позволяет избежать потери корней. Каким конкретно числом должно быть новое основание логарифмов всегда можно понять, проанализировав данное уравнение.Так в рассмотренном выше примере, подходящим новым основанием логарифмов является число 2. Это следует из того, что все входящие в уравнения основания логарифмов имеют вид:
.Применяя при решении логарифмических уравнений формулы перехода к новому основанию целесообразней переходить к новому основанию не являющемуся выражением с переменной, а равному некоторому числу. Как правило, это позволяет избежать потери корней. Каким конкретно числом должно быть новое основание логарифмов всегда можно понять, проанализировав данное уравнение.Так в рассмотренном выше примере, подходящим новым основанием логарифмов является число 2. Это следует из того, что все входящие в уравнения основания логарифмов имеют вид: 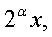 где
где 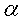 — целое число.Далее, с учетом этого замечания оформим решение уравнения из примера 6 как схему равносильных переходов.
— целое число.Далее, с учетом этого замечания оформим решение уравнения из примера 6 как схему равносильных переходов.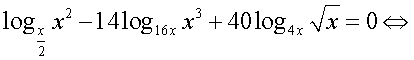
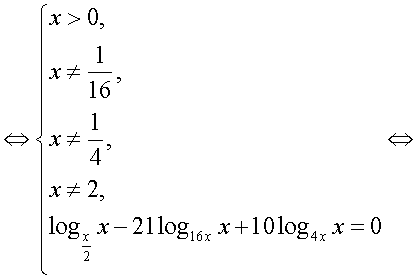
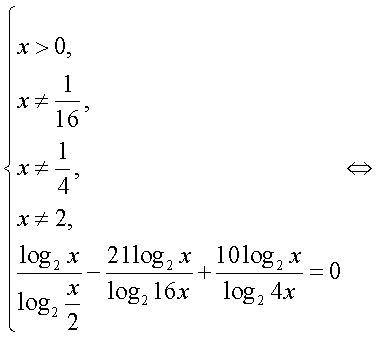
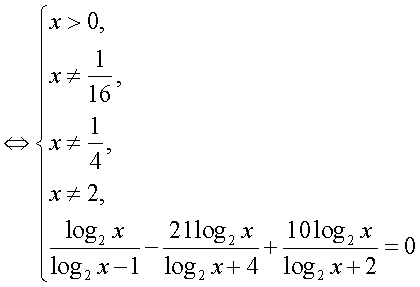
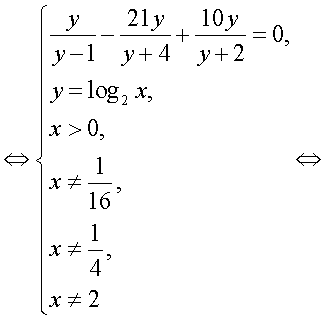
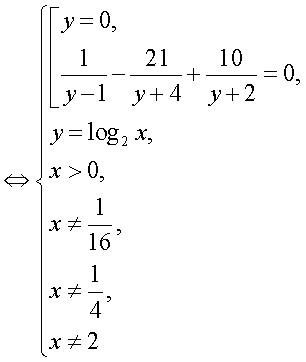
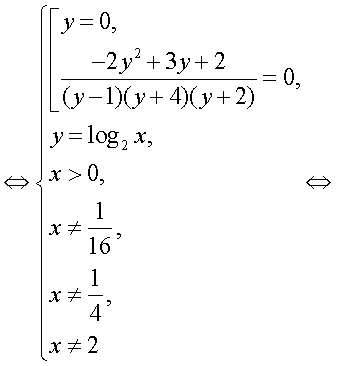
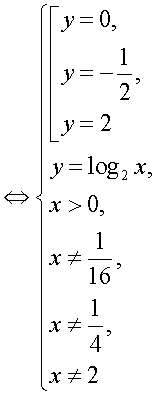
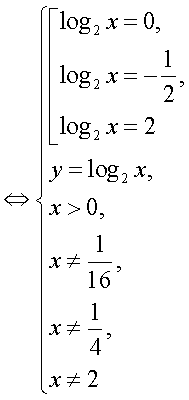
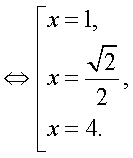 Еще раз следует отметить, что решение любого уравнения должно осуществляться не механически, а сознательно, с пониманием сущности всех преобразований, с обязательным анализом возможностей появления посторонних корней и потери корней. Если такой анализ непосредственно «вплетен» в ход решения, то наиболее действенно оформлять это решение схемой равносильных переходов. Хотя это и приводит, порой, к весьма громоздким записям. Громоздкости при записи решения уравнения в виде схемы равносильных переходов можно избежать следующим приемом: начать решение уравнения с нахождения области определения и затем при проведении решения соблюдать не «равносильность вообще», а «равносильность на области определения». Оформим решение уравнения из примера 6 с учетом этого приема.
Еще раз следует отметить, что решение любого уравнения должно осуществляться не механически, а сознательно, с пониманием сущности всех преобразований, с обязательным анализом возможностей появления посторонних корней и потери корней. Если такой анализ непосредственно «вплетен» в ход решения, то наиболее действенно оформлять это решение схемой равносильных переходов. Хотя это и приводит, порой, к весьма громоздким записям. Громоздкости при записи решения уравнения в виде схемы равносильных переходов можно избежать следующим приемом: начать решение уравнения с нахождения области определения и затем при проведении решения соблюдать не «равносильность вообще», а «равносильность на области определения». Оформим решение уравнения из примера 6 с учетом этого приема.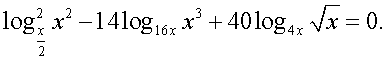 Область определения этого уравнения (множество М):
Область определения этого уравнения (множество М):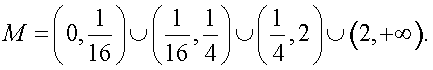 Далее, имеем:
Далее, имеем: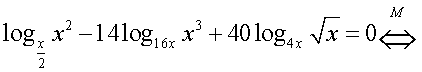
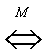
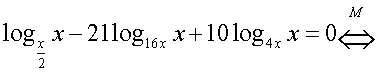
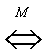
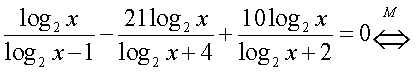
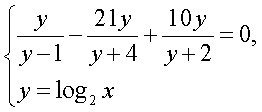
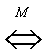
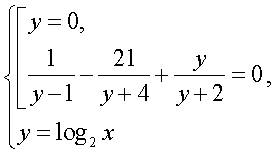
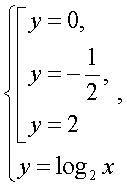
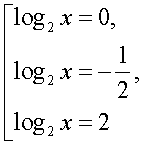
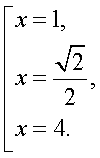 Оформим также в виде равносильных переходов решение уравнений из следующих примеров. Эти уравнения (весьма распространенные в заданиях ЕГЭ, группа С), содержащие логарифмы, у которых и основания, и логарифмируемые выражения — выражения с переменной.Пример 14. Решим уравнение:
Оформим также в виде равносильных переходов решение уравнений из следующих примеров. Эти уравнения (весьма распространенные в заданиях ЕГЭ, группа С), содержащие логарифмы, у которых и основания, и логарифмируемые выражения — выражения с переменной.Пример 14. Решим уравнение: 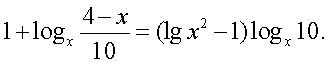 Решение.Область определения этого уравнения (множество М):
Решение.Область определения этого уравнения (множество М):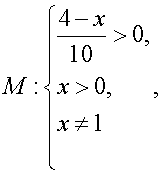 т.е.
т.е. 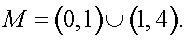 Далее, имеем:
Далее, имеем: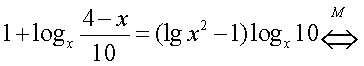
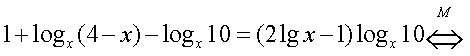
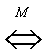
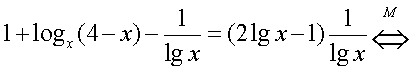
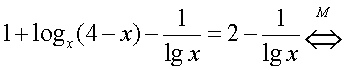
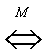
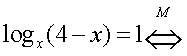
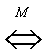
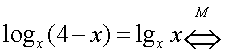
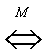
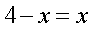
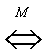
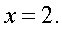 Ответ: 2.Пример 15.Ответ: а) Ш; б) 1.Часто трудности с решением рациональных уравнений
Ответ: 2.Пример 15.Ответ: а) Ш; б) 1.Часто трудности с решением рациональных уравнений обусловлены для абитуриентов тем, что решение, как говорится «в лоб», по алгоритму метода разложения на множители
обусловлены для абитуриентов тем, что решение, как говорится «в лоб», по алгоритму метода разложения на множители :
: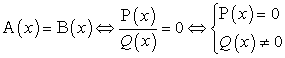 ,где A (x), B (x) — произвольные рациональные выражения; P (x), Q (x) — многочлены,приводит к громоздким, «рутинным» преобразованиям или к необходимости находить корни многочленов степени большей, чем второй. А это уже не совсем «школьная» задача. При этом даже в самых очевидных случаях, абитуриенты не применяют метод введения новой переменной
,где A (x), B (x) — произвольные рациональные выражения; P (x), Q (x) — многочлены,приводит к громоздким, «рутинным» преобразованиям или к необходимости находить корни многочленов степени большей, чем второй. А это уже не совсем «школьная» задача. При этом даже в самых очевидных случаях, абитуриенты не применяют метод введения новой переменной . А ведь введение новой переменной позволяет быстро упростить решаемое уравнение. Это мощный метод, его следует понимать и применять.Введение новой переменной осуществляется тогда, когда решаемое уравнение представимо в виде f (g (x)) = 0. Полагая g (x) = t, мы переходим к решению системы:
. А ведь введение новой переменной позволяет быстро упростить решаемое уравнение. Это мощный метод, его следует понимать и применять.Введение новой переменной осуществляется тогда, когда решаемое уравнение представимо в виде f (g (x)) = 0. Полагая g (x) = t, мы переходим к решению системы: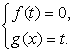 Если уравнения f (t) = 0, g(x) = t1 , g(x) = t2,…, g (x) = tn, где t1, t2,…, tn — корни уравнения f (t) = 0 проще исходного уравнения, то метод, как говорится, сработал.Рассмотрим различные рациональные уравнения, для решения которых весьма полезен метод введения новой переменной, но не очевидны случаи, когда исходное уравнение непосредственно имеет вид f (g(x)) = 0. Поиск удачной подстановки g (x) = t и специальная работа по приведению исходного уравнения к указанному виду, составляет главную сущностную часть решения уравнения. Решение же уравнения f (t) = 0 и совокупности уравнений g (x) = ti — сравнительно несложная, техническая часть процесса решения уравнения.Решение дробно-рациональных уравнений
Если уравнения f (t) = 0, g(x) = t1 , g(x) = t2,…, g (x) = tn, где t1, t2,…, tn — корни уравнения f (t) = 0 проще исходного уравнения, то метод, как говорится, сработал.Рассмотрим различные рациональные уравнения, для решения которых весьма полезен метод введения новой переменной, но не очевидны случаи, когда исходное уравнение непосредственно имеет вид f (g(x)) = 0. Поиск удачной подстановки g (x) = t и специальная работа по приведению исходного уравнения к указанному виду, составляет главную сущностную часть решения уравнения. Решение же уравнения f (t) = 0 и совокупности уравнений g (x) = ti — сравнительно несложная, техническая часть процесса решения уравнения.Решение дробно-рациональных уравнений нередко сводится к решению обычных квадратных уравнений, но с учетом ограничений на допустимые значения неизвестного. В частности, из ОДЗ исключаются те значения х, при которых хотя бы один из знаменателей дробей, входящих в уравнение, обращается в 0.Этапы решения рационального уравнения
нередко сводится к решению обычных квадратных уравнений, но с учетом ограничений на допустимые значения неизвестного. В частности, из ОДЗ исключаются те значения х, при которых хотя бы один из знаменателей дробей, входящих в уравнение, обращается в 0.Этапы решения рационального уравнения .
.- Определить ОДЗ (ни один знаменатель не может равняться нулю).
- Найти наименьший общий знаменатель всех дробей.
- Умножить уравнение на этот знаменатель и решить полученное целое уравнение.
- Включить в ответ только те корни, которые входят в ОДЗ.
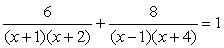 Решение.Раскрыв скобки в знаменателях, получаем уравнение:
Решение.Раскрыв скобки в знаменателях, получаем уравнение: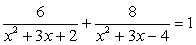 Полагая, что x2 + 3х + 2 = t приходим к системе уравнений:
Полагая, что x2 + 3х + 2 = t приходим к системе уравнений: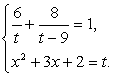 Решив первое уравнение системы, получаем корни t1 = 2, t1 = 18. Далее, из второго уравнения системы, получаем корни исходного уравнения:
Решив первое уравнение системы, получаем корни t1 = 2, t1 = 18. Далее, из второго уравнения системы, получаем корни исходного уравнения: 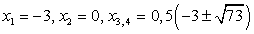 .Ответ:
.Ответ: 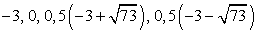 .Пример 17.Решим уравнение:
.Пример 17.Решим уравнение:  .Решение.Прибавим к числителю второй дроби выражение 2х - 2х, тождественно равное нулю:
.Решение.Прибавим к числителю второй дроби выражение 2х - 2х, тождественно равное нулю: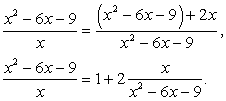 Полагая
Полагая 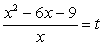 , приходим к системе уравнений:
, приходим к системе уравнений: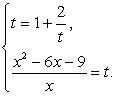 Решив первое уравнение системы, получаем корни: t1 = -1, t2 = 2. Из второго уравнения системы, получаем корни исходного уравнения:
Решив первое уравнение системы, получаем корни: t1 = -1, t2 = 2. Из второго уравнения системы, получаем корни исходного уравнения: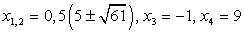 Ответ:
Ответ: 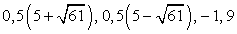 Пример 18.Решим уравнение:
Пример 18.Решим уравнение: 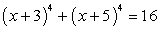 Решение.Полагая, что
Решение.Полагая, что 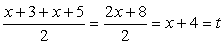 , приходим к системе уравнений:
, приходим к системе уравнений: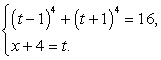 Решим первое уравнение системы, воспользовавшись формулой:
Решим первое уравнение системы, воспользовавшись формулой: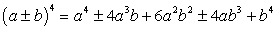 Имеем:
Имеем: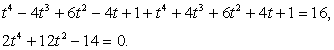 Решив полученное биквадратное уравнение, получаем корни t1, 2 = ± 1 и соответственно: x1 = -5, x2 = -3.Ответ: -5; -3.Пример 19.Решим уравнение:
Решив полученное биквадратное уравнение, получаем корни t1, 2 = ± 1 и соответственно: x1 = -5, x2 = -3.Ответ: -5; -3.Пример 19.Решим уравнение: 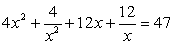 Решение.Принимая во внимание тождество
Решение.Принимая во внимание тождество 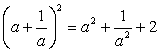 , перепишем данное уравнение в виде:
, перепишем данное уравнение в виде: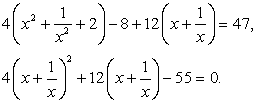 Полагая, что
Полагая, что 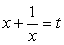 , имеем систему уравнений:4t2 + 12t - 55 = 0,
, имеем систему уравнений:4t2 + 12t - 55 = 0,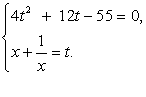 Решив первое уравнение системы, получаем корни:
Решив первое уравнение системы, получаем корни: 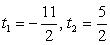 .Из второго уравнения системы получаем корни исходного уравнения:
.Из второго уравнения системы получаем корни исходного уравнения: 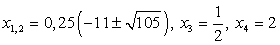 .Ответ:
.Ответ: 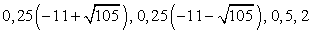 Пример 20.Решим уравнение:
Пример 20.Решим уравнение: 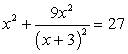 Решение.Левая часть уравнения представляет собой сумму квадратов. Для решения уравнения, удобно превратить ее в полный квадрат, добавив к обеим частям уравнения соответствующее удвоенное произведение:
Решение.Левая часть уравнения представляет собой сумму квадратов. Для решения уравнения, удобно превратить ее в полный квадрат, добавив к обеим частям уравнения соответствующее удвоенное произведение: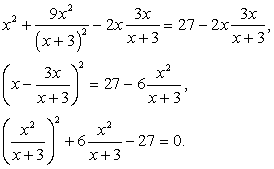 Полагая, что
Полагая, что 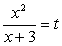 , имеем систему уравнений:
, имеем систему уравнений: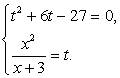 Решив первое уравнение системы, получаем корни t1 = -9, t2 = 3. Далее, из второго уравнения системы, получаем корни исходного уравнения:
Решив первое уравнение системы, получаем корни t1 = -9, t2 = 3. Далее, из второго уравнения системы, получаем корни исходного уравнения: 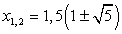 .Пример 21.Решим уравнение:
.Пример 21.Решим уравнение: 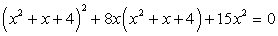 Решение.Положим, что x2 + х + 4 = t. Тогда заданное уравнение принимает вид:t2 + 8xt + 15x2 = 0.Решив это уравнение как квадратное относительно t, получаем:
Решение.Положим, что x2 + х + 4 = t. Тогда заданное уравнение принимает вид:t2 + 8xt + 15x2 = 0.Решив это уравнение как квадратное относительно t, получаем: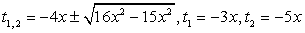 Совокупность уравнений:
Совокупность уравнений: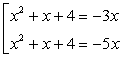 дает корни исходного уравнения:
дает корни исходного уравнения: 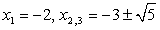 Ответ:
Ответ: 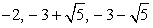 .Метод введения новой переменной
.Метод введения новой переменной иногда называют методом замены переменной. Это не совсем правомерно. Введение новой переменной в уравнение отнюдь не предполагает обязательное исчезновение из уравнения старой переменной.Пример 22.Решим уравнение:
иногда называют методом замены переменной. Это не совсем правомерно. Введение новой переменной в уравнение отнюдь не предполагает обязательное исчезновение из уравнения старой переменной.Пример 22.Решим уравнение: 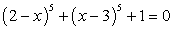 Решение.Пусть x0 — корень уравнения. Введем новые неизвестные u = 2 - x0 и х = x0 - 3. Понятно, что термин «новые переменные» в данном случае был бы применен неправильно. U и v — хотя и неизвестные, но постоянные величины, ибо х0 — постоянная, а отнюдь не переменная величина.Имеем систему уравнений:
Решение.Пусть x0 — корень уравнения. Введем новые неизвестные u = 2 - x0 и х = x0 - 3. Понятно, что термин «новые переменные» в данном случае был бы применен неправильно. U и v — хотя и неизвестные, но постоянные величины, ибо х0 — постоянная, а отнюдь не переменная величина.Имеем систему уравнений: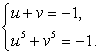 Воспользовавшись формулой:
Воспользовавшись формулой: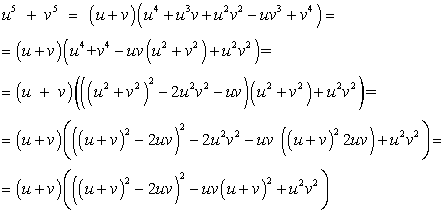 ,имеем:
,имеем: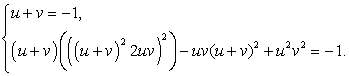 Учитывая, что u + v = -1, из второго уравнения системы получаем:
Учитывая, что u + v = -1, из второго уравнения системы получаем: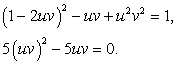 Таким образом, либо uv = 1, либо uv = 0 и для нахождения u и v имеем две системы уравнений (совокупность систем):
Таким образом, либо uv = 1, либо uv = 0 и для нахождения u и v имеем две системы уравнений (совокупность систем):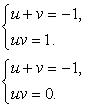 Первая система решений не имеет.Корни второй системы: u1 = 0, v1 = -1 и u2 = -1, v2 = 0. Отсюда либо x0 = 2, либо x0 = 3.Итак, корни исходного уравнения: x1 = 2, x2 = 3.Ответ: 2; 3.Весьма распространенный прием решения иррациональных уравнений и неравенств — возведение в квадрат
Первая система решений не имеет.Корни второй системы: u1 = 0, v1 = -1 и u2 = -1, v2 = 0. Отсюда либо x0 = 2, либо x0 = 3.Итак, корни исходного уравнения: x1 = 2, x2 = 3.Ответ: 2; 3.Весьма распространенный прием решения иррациональных уравнений и неравенств — возведение в квадрат . Тем не менее, советуем вам пользоваться им как можно реже, ибо он обладает существенными недостатками: во-первых, возводя в квадрат обе части уравнения, вы расширяете область допустимых значений неизвестного, что может привести к появлению посторонних корней
. Тем не менее, советуем вам пользоваться им как можно реже, ибо он обладает существенными недостатками: во-первых, возводя в квадрат обе части уравнения, вы расширяете область допустимых значений неизвестного, что может привести к появлению посторонних корней ; во-вторых, часто в результате этой операции получается уравнение с громоздкими коэффициентами, работать с которыми затруднительно (особенно если на экзамене не разрешается пользоваться калькулятором). Наконец, главный недостаток этого приема — увеличение вдвое степени уравнения. Возведя обе части в квадрат, вы можете избавиться от иррациональностей, но получить рациональное уравнение степени выше второй, способы решения которого в общем виде вам неизвестны или вообще не существуют.Если возводить в квадрат все-таки приходится, нужно внимательно следить за тем, чтобы не включить в ответ посторонние корни. В частности, если уравнение имеет вид
; во-вторых, часто в результате этой операции получается уравнение с громоздкими коэффициентами, работать с которыми затруднительно (особенно если на экзамене не разрешается пользоваться калькулятором). Наконец, главный недостаток этого приема — увеличение вдвое степени уравнения. Возведя обе части в квадрат, вы можете избавиться от иррациональностей, но получить рациональное уравнение степени выше второй, способы решения которого в общем виде вам неизвестны или вообще не существуют.Если возводить в квадрат все-таки приходится, нужно внимательно следить за тем, чтобы не включить в ответ посторонние корни. В частности, если уравнение имеет вид 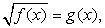 то для корней должно выполняться условие
то для корней должно выполняться условие 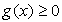 (при этом
(при этом 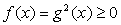 , и условие
, и условие 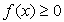 отдельно ставить не требуется). Еще один способ обнаружить посторонние корни — проверка всех найденных корней подстановкой их в первоначальное уравнение.Пример 23.Решить уравнение:
отдельно ставить не требуется). Еще один способ обнаружить посторонние корни — проверка всех найденных корней подстановкой их в первоначальное уравнение.Пример 23.Решить уравнение: 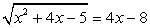 .Решение.Корни должны удовлетворять условию 4х - 8 ≥
0, то есть х ≥
2. Возведем обе части в квадрат:
.Решение.Корни должны удовлетворять условию 4х - 8 ≥
0, то есть х ≥
2. Возведем обе части в квадрат: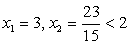 — посторонний корень.Ответ: х = 3.Пример 24.
— посторонний корень.Ответ: х = 3.Пример 24.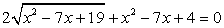 .Поскольку неизвестное входит в подкоренное выражение и в рациональную часть уравнения в виде одной и той же комбинации (x2 - 7х), можно сделать замену:
.Поскольку неизвестное входит в подкоренное выражение и в рациональную часть уравнения в виде одной и той же комбинации (x2 - 7х), можно сделать замену: 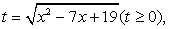 , тогда x2 - 7х = t2 - 19, и t определяется из уравнения: 2t + t2 - 19 + 4 = 0, t2 + 2t - 15 = 0, t1 = 3, t2 = - 5 < 0 — не соответствует условию на знак t.Обратная замена:
, тогда x2 - 7х = t2 - 19, и t определяется из уравнения: 2t + t2 - 19 + 4 = 0, t2 + 2t - 15 = 0, t1 = 3, t2 = - 5 < 0 — не соответствует условию на знак t.Обратная замена: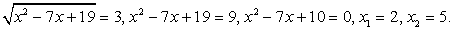 Ответ: х = 2, х = 5.Замена переменной
Ответ: х = 2, х = 5.Замена переменной очень полезна при решении иррациональных уравнений. Часто с ее помощью удается избежать необходимости возведения в квадрат.Пример 25.Решить уравнение:
очень полезна при решении иррациональных уравнений. Часто с ее помощью удается избежать необходимости возведения в квадрат.Пример 25.Решить уравнение: 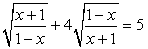 .Решение.Подкоренные выражения — взаимно обратные дроби, поэтому замена
.Решение.Подкоренные выражения — взаимно обратные дроби, поэтому замена 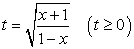 приводит к уравнению:
приводит к уравнению: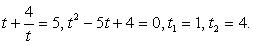 Случай 1.
Случай 1. 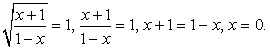 Случай 2.
Случай 2. 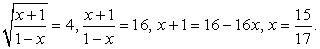 Ответ:
Ответ: 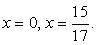 Следует обратить внимание на то, что в некоторых заданиях нет необходимости в проверке корней или задании каких-либо ограничений: значения х определяются из условия, что корень принимает некоторое неотрицательное значение.Пример 26.Решить уравнение:
Следует обратить внимание на то, что в некоторых заданиях нет необходимости в проверке корней или задании каких-либо ограничений: значения х определяются из условия, что корень принимает некоторое неотрицательное значение.Пример 26.Решить уравнение: 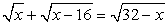 .Решение.Перепишем уравнение в виде:
.Решение.Перепишем уравнение в виде: 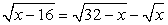 и возведем обе части в квадрат, не задавая никаких ограничений: проще будет в конце работы проверить получившиеся корни:
и возведем обе части в квадрат, не задавая никаких ограничений: проще будет в конце работы проверить получившиеся корни: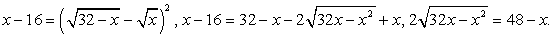 Еще раз возведем в квадрат обе части полученного равенства:
Еще раз возведем в квадрат обе части полученного равенства: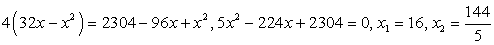 .Проверка.
.Проверка.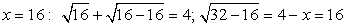 — корень уравнения.
— корень уравнения.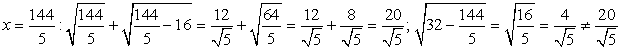 —
— 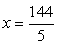 — не корень уравнения.Ответ: х = 16.Пример 27.Решить уравнение:
— не корень уравнения.Ответ: х = 16.Пример 27.Решить уравнение: 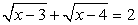 .В этом уравнении замена
.В этом уравнении замена 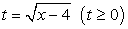 поможет ограничиться только одним возведением в квадрат: Ответ:
поможет ограничиться только одним возведением в квадрат: Ответ: 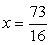 .Пример 28.
.Пример 28.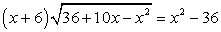 .Решение.ОДЗ задается условием:
.Решение.ОДЗ задается условием: 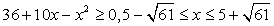 . Запишем уравнение в виде:
. Запишем уравнение в виде: 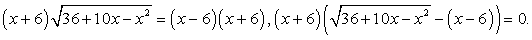
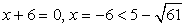 — посторонний корень.
— посторонний корень.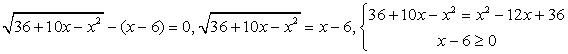 ,
,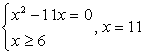 (корень первого уравнения х = 0 не удовлетворяет второму условию). Итак, единственный корень исходного уравнения — х = 11.Ответ: х = 11.Рассмотренные совокупности решаются просто, но в более сложных случаях обязательное соблюдение условия равносильности преобразований может привести к серьезным техническим трудностям, сделать решение слишком ветвящимся и громоздким. Поэтому, не будем строго запрещать применение любых неравносильных преобразований. Все ли они одинаково опасны? Понятно, что более опасны неравносильные преобразования, приводящие к потере корней. В большинстве случаев потерянные корни отыскать весьма трудно (заметим также, что малоопытный решающий, а абитуриент часто именно таков, может вовсе не заметить факта потери корня, и не будет пытаться его отыскать, хотя это, может быть, и получилось бы).Итак, на не равносильные преобразования, приводящие к потере корней, мы накладываем строгий и категорический запрет. При решении уравнений, таким образом, мы не будем применять деление обеих частей уравнения на выражение, обращающееся в ноль в области определения уравнения, и не будем применять преобразования, приводящие к сужению области определения уравнения.Что же касается, неравносильных преобразований, приводящих к появлению посторонних корней, то такие преобразования вполне допустимы. Но при этом, обязательным заключительным этапом решения должна быть проверка всех найденных в итоге корней. Заметим, что тактика проверки зависит непосредственно от класса уравнений (рациональные, иррациональные, логарифмические и т.д.), ибо в каждом случае свои причины появления посторонних корней. В этой связи, тактика проверки конечно должна быть гибкой, но можно пользоваться и универсальным приемом: подстановка всех корней итогового уравнения в исходное с последующим вычислением или «прикидкой».Пример 29.Решим уравнение:
(корень первого уравнения х = 0 не удовлетворяет второму условию). Итак, единственный корень исходного уравнения — х = 11.Ответ: х = 11.Рассмотренные совокупности решаются просто, но в более сложных случаях обязательное соблюдение условия равносильности преобразований может привести к серьезным техническим трудностям, сделать решение слишком ветвящимся и громоздким. Поэтому, не будем строго запрещать применение любых неравносильных преобразований. Все ли они одинаково опасны? Понятно, что более опасны неравносильные преобразования, приводящие к потере корней. В большинстве случаев потерянные корни отыскать весьма трудно (заметим также, что малоопытный решающий, а абитуриент часто именно таков, может вовсе не заметить факта потери корня, и не будет пытаться его отыскать, хотя это, может быть, и получилось бы).Итак, на не равносильные преобразования, приводящие к потере корней, мы накладываем строгий и категорический запрет. При решении уравнений, таким образом, мы не будем применять деление обеих частей уравнения на выражение, обращающееся в ноль в области определения уравнения, и не будем применять преобразования, приводящие к сужению области определения уравнения.Что же касается, неравносильных преобразований, приводящих к появлению посторонних корней, то такие преобразования вполне допустимы. Но при этом, обязательным заключительным этапом решения должна быть проверка всех найденных в итоге корней. Заметим, что тактика проверки зависит непосредственно от класса уравнений (рациональные, иррациональные, логарифмические и т.д.), ибо в каждом случае свои причины появления посторонних корней. В этой связи, тактика проверки конечно должна быть гибкой, но можно пользоваться и универсальным приемом: подстановка всех корней итогового уравнения в исходное с последующим вычислением или «прикидкой».Пример 29.Решим уравнение: 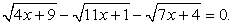 При решении этого уравнения будем придерживаться стратегии, допускающей неравносильные преобразования при обязательной проверке корней. Решая уравнения вида
При решении этого уравнения будем придерживаться стратегии, допускающей неравносильные преобразования при обязательной проверке корней. Решая уравнения вида 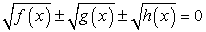 , следует перед возведением в квадрат уединить один из корней, перенеся его в правую часть уравнения. Уединить можно любой из корней, и в большинстве случаев, все равно какой. Но иногда уединение определенного корня приводит к более простому решению, чем уединение других. Поэтому всегда следует анализировать ситуацию в указанном аспекте.Решение.В нашем уравнение сумма коэффициентов при х в первом и третьем подкоренных выражениях равна коэффициенту при х во втором подкоренном выражении. Поэтому уединить целесообразно именно корень
, следует перед возведением в квадрат уединить один из корней, перенеся его в правую часть уравнения. Уединить можно любой из корней, и в большинстве случаев, все равно какой. Но иногда уединение определенного корня приводит к более простому решению, чем уединение других. Поэтому всегда следует анализировать ситуацию в указанном аспекте.Решение.В нашем уравнение сумма коэффициентов при х в первом и третьем подкоренных выражениях равна коэффициенту при х во втором подкоренном выражении. Поэтому уединить целесообразно именно корень 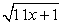 . Полученное после возведения в квадрат уравнение будет содержать х только под корнем. Если бы мы уединяли любой из других корней, то после возведения в квадрат получали бы уравнения, содержащие х и под корнем, и вне корня, что менее удобно для последующего решения.Итак, имеем:
. Полученное после возведения в квадрат уравнение будет содержать х только под корнем. Если бы мы уединяли любой из других корней, то после возведения в квадрат получали бы уравнения, содержащие х и под корнем, и вне корня, что менее удобно для последующего решения.Итак, имеем: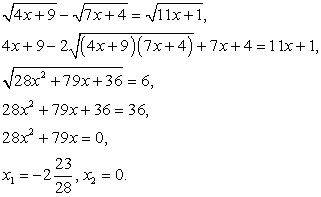 При решении иррационального уравнения мы осуществляем так называемую рационализацию уравнения, т.е. избавляемся от радикалов (корней). Но, избавляясь от корней, мы избавляемся и от ограничений на подкоренные выражения:
При решении иррационального уравнения мы осуществляем так называемую рационализацию уравнения, т.е. избавляемся от радикалов (корней). Но, избавляясь от корней, мы избавляемся и от ограничений на подкоренные выражения: 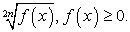 Иными словами, происходит расширение области определения уравнения. Это причина появления посторонних корней. Поэтому все корни итогового уравнения, полученного в ходе решение, следует проверить на принадлежность области определения исходного уравнения. В нашем случае область определения исходного уравнения задается системой:
Иными словами, происходит расширение области определения уравнения. Это причина появления посторонних корней. Поэтому все корни итогового уравнения, полученного в ходе решение, следует проверить на принадлежность области определения исходного уравнения. В нашем случае область определения исходного уравнения задается системой: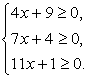 Решив эту систему, получаем область определения уравнения:
Решив эту систему, получаем область определения уравнения: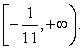 Очевидно, что
Очевидно, что 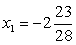 — посторонний корень, появившийся в процессе решения из-за применения неравносильных преобразований, приведших к расширению области определения уравнения, а x2 = 0 — принадлежит области определения уравнения и является его корнем (что легко проверить непосредственной подстановкой).Ответ: х = 0.Но единственная ли причина появления посторонних корней при решении иррациональных уравнений с радикалами четной степени — расширение области определения исходного уравнения? Не кроется ли в возведении обеих частей уравнения в четную степень еще одна, менее очевидная, но не менее опасная в смысле ошибки, причина появления посторонних корней?Пример 30.а) Решим уравнение:
— посторонний корень, появившийся в процессе решения из-за применения неравносильных преобразований, приведших к расширению области определения уравнения, а x2 = 0 — принадлежит области определения уравнения и является его корнем (что легко проверить непосредственной подстановкой).Ответ: х = 0.Но единственная ли причина появления посторонних корней при решении иррациональных уравнений с радикалами четной степени — расширение области определения исходного уравнения? Не кроется ли в возведении обеих частей уравнения в четную степень еще одна, менее очевидная, но не менее опасная в смысле ошибки, причина появления посторонних корней?Пример 30.а) Решим уравнение: 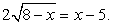 При решении этого уравнения будем придерживаться стратегии, допускающей неравносильные преобразования, т.е. возведем обе части уравнения в квадрат, решим полученное рациональное уравнение и сделаем проверку корней.Итак,
При решении этого уравнения будем придерживаться стратегии, допускающей неравносильные преобразования, т.е. возведем обе части уравнения в квадрат, решим полученное рациональное уравнение и сделаем проверку корней.Итак, 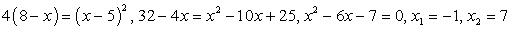 Проверим, удовлетворяют ли эти корни исходному уравнению.Пусть х = -1, тогда левая часть исходного уравнения равна -6. Таким образом, х = -1 — посторонний для исходного уравнения корень, появившийся в процессе решения из-за применения неравносильных преобразований. Пусть теперь, х = 7. Тогда исходное уравнение превращается в верное числовое равенство. Исходное уравнение, таким образом, имеет единственный корень х = 7.б) Решим теперь уравнение
Проверим, удовлетворяют ли эти корни исходному уравнению.Пусть х = -1, тогда левая часть исходного уравнения равна -6. Таким образом, х = -1 — посторонний для исходного уравнения корень, появившийся в процессе решения из-за применения неравносильных преобразований. Пусть теперь, х = 7. Тогда исходное уравнение превращается в верное числовое равенство. Исходное уравнение, таким образом, имеет единственный корень х = 7.б) Решим теперь уравнение 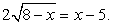 (его чрезвычайно, малое отличие от предыдущего уравнения очевидно).Поступая так же, как в случае «а», получаем:
(его чрезвычайно, малое отличие от предыдущего уравнения очевидно).Поступая так же, как в случае «а», получаем: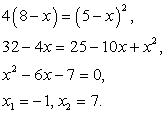 Итоговое уравнение имеет такие же корни, что и уравнение из случая «а». Проверим их подстановкой в исходное уравнение
Итоговое уравнение имеет такие же корни, что и уравнение из случая «а». Проверим их подстановкой в исходное уравнение 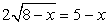 . Пусть х = -1, тогда исходное уравнение превращается в верное числовое равенство. Пусть, далее, х = 7. Тогда левая часть исходного уравнения равна -2. Таким образом, х = 7 — посторонний для исходного уравнения корень.В процессе решения следствием уравнений «а», «б» является одно и тоже уравнение
. Пусть х = -1, тогда исходное уравнение превращается в верное числовое равенство. Пусть, далее, х = 7. Тогда левая часть исходного уравнения равна -2. Таким образом, х = 7 — посторонний для исходного уравнения корень.В процессе решения следствием уравнений «а», «б» является одно и тоже уравнение 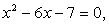 имеющее два корня: x1 = -1 и x2 = 7. Корень x1 = -1 — есть корень уравнения «б», но посторонний для уравнения «а»; корень x2 = 7 — наоборот, корень уравнения «а», посторонний для уравнения «б».В каждом из случаев «а» и «б» корни, оказавшиеся посторонними, принадлежат области определения данного уравнения. Значит, расширение области определения исходного уравнения — не единственная причина появления посторонних корней. В чем же дело? Заметим, что и в случае «а», и в случае «б» при подстановке в исходное уравнение корень, оказывающийся посторонним, приводит к ситуации: левая и правая части уравнения равны по абсолютной величине, но противоположны по знаку. Это не случайно. Уравнение
имеющее два корня: x1 = -1 и x2 = 7. Корень x1 = -1 — есть корень уравнения «б», но посторонний для уравнения «а»; корень x2 = 7 — наоборот, корень уравнения «а», посторонний для уравнения «б».В каждом из случаев «а» и «б» корни, оказавшиеся посторонними, принадлежат области определения данного уравнения. Значит, расширение области определения исходного уравнения — не единственная причина появления посторонних корней. В чем же дело? Заметим, что и в случае «а», и в случае «б» при подстановке в исходное уравнение корень, оказывающийся посторонним, приводит к ситуации: левая и правая части уравнения равны по абсолютной величине, но противоположны по знаку. Это не случайно. Уравнение 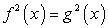 является следствием не только уравнения
является следствием не только уравнения 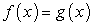 , но и следствием уравнения
, но и следствием уравнения 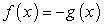 . Какие следует сделать из этого выводы?Во-первых, поскольку появление посторонних корней при решении иррациональных уравнений, содержащих радикалы четной степени может быть и не связано с областью определения исходного уравнения, то и проверка корней не может осуществляться только по области определения, или условиям ее задающим.Во-вторых, проверка корней иррационального уравнения, должна учитывать обе причины появления посторонних корней; универсальный прием, как уже говорилось, состоит в непосредственной подстановке в исходное уравнение, но могут быть реализованы и другие подходы.
. Какие следует сделать из этого выводы?Во-первых, поскольку появление посторонних корней при решении иррациональных уравнений, содержащих радикалы четной степени может быть и не связано с областью определения исходного уравнения, то и проверка корней не может осуществляться только по области определения, или условиям ее задающим.Во-вторых, проверка корней иррационального уравнения, должна учитывать обе причины появления посторонних корней; универсальный прием, как уже говорилось, состоит в непосредственной подстановке в исходное уравнение, но могут быть реализованы и другие подходы.- Сначала отсечь те корни, которые не принадлежат области определения исходного уравнения, а оставшиеся проверить непосредственной подстановкой во все уравнения левая и правая части которых возводились в квадрат в процессе решения.
- Опять же исключить все корни, не принадлежащие области определения, а затем проанализировать все случаи возведения в квадрат обеих частей уравнения, выделить те случаи, где было нарушено условие равносильности:
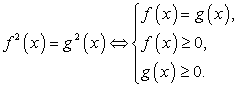 Далее только в эти уравнения подставить корни итогового уравнения, принадлежащие области определения исходного уравнения.
Далее только в эти уравнения подставить корни итогового уравнения, принадлежащие области определения исходного уравнения. - Если решать иррациональные уравнения, применяя только равносильные преобразования, то в каждом случае возведения в квадрат следует предусматривать условие равносильности, сформулированное выше, и изначально следует зафиксировать условия, задающие область определения исходного уравнения.
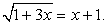 Решение.Возведя обе части уравнения в квадрат, получаем 1 + 3х = x2 + 2х + 1, т.е. уравнение x2 – х = 0. Его корни x1 = 0 и x2 = 1. Подставляя каждый из найденных корней в исходное уравнение, убеждаемся, что оба они являются его корнями.Пример 32.Решим уравнение:
Решение.Возведя обе части уравнения в квадрат, получаем 1 + 3х = x2 + 2х + 1, т.е. уравнение x2 – х = 0. Его корни x1 = 0 и x2 = 1. Подставляя каждый из найденных корней в исходное уравнение, убеждаемся, что оба они являются его корнями.Пример 32.Решим уравнение: 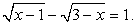 Решение.Уединим радикалы:
Решение.Уединим радикалы: 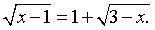 Возведем обе части уравнения в квадрат (дважды):
Возведем обе части уравнения в квадрат (дважды):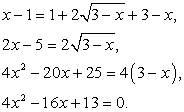 Корни последнего уравнения:
Корни последнего уравнения: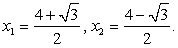 Далее следует провести проверку корней. Область определения исходного уравнения задается условиями
Далее следует провести проверку корней. Область определения исходного уравнения задается условиями 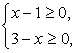 т.е. 1 ≤
x ≤
3. Как нетрудно проверить, полагая
т.е. 1 ≤
x ≤
3. Как нетрудно проверить, полагая 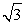 приближенно равным 1,7, что оба корня x1 и x2 принадлежат области определения исходного уравнения. Значит, если среди x1 и x2 есть посторонний корень, то причина его появления связана с нарушением условия равносильного возведения обеих частей уравнения в квадрат. Ясно, также, что первое из проделанных в данном решении возведений в квадрат — равносильное преобразование, поэтому если и появились посторонние корни, то при возведении в квадрат обеих частей уравнения
приближенно равным 1,7, что оба корня x1 и x2 принадлежат области определения исходного уравнения. Значит, если среди x1 и x2 есть посторонний корень, то причина его появления связана с нарушением условия равносильного возведения обеих частей уравнения в квадрат. Ясно, также, что первое из проделанных в данном решении возведений в квадрат — равносильное преобразование, поэтому если и появились посторонние корни, то при возведении в квадрат обеих частей уравнения 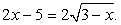 Непосредственной подстановкой именно в это уравнение проверим наши корни x1 и x2.Итак, пусть
Непосредственной подстановкой именно в это уравнение проверим наши корни x1 и x2.Итак, пусть 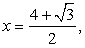 тогда:
тогда: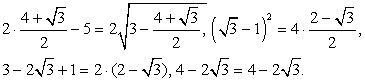 Мы пришли к верному числовому равенству. Значит
Мы пришли к верному числовому равенству. Значит 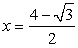 — корень данного уравнения.Пусть теперь
— корень данного уравнения.Пусть теперь 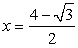 Тогда
Тогда 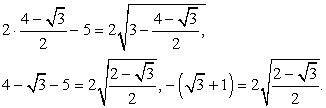 Ясно, что левая часть уравнения отрицательна, а правая положительна. Поэтому
Ясно, что левая часть уравнения отрицательна, а правая положительна. Поэтому 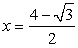 — посторонний корень.Пример 33.Решим уравнение:
— посторонний корень.Пример 33.Решим уравнение: 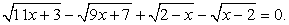 Распределим радикалы следующим образом:
Распределим радикалы следующим образом: 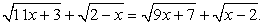 Возведем обе части уравнения в квадрат и приведем подобные слагаемые:
Возведем обе части уравнения в квадрат и приведем подобные слагаемые: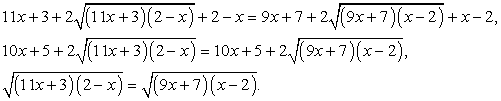 Возведем обе части полученного уравнения в квадрат, раскроем скобки и приведем подобные слагаемые:
Возведем обе части полученного уравнения в квадрат, раскроем скобки и приведем подобные слагаемые: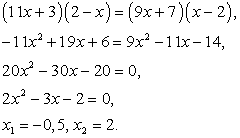 Проведем проверку корней. Сразу замечаем, что корень
Проведем проверку корней. Сразу замечаем, что корень 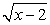 не имеет смысла при x = -0,5. Поэтому единственный возможный корень исходного уравнения — это х = 2, удовлетворяющий всем условиям области определения. Поскольку, возводя обе части уравнения в квадрат, мы всякий раз соблюдали условие равносильности, то х = 2 — единственный корень исходного уравнения.Пример 34.Решим уравнение:
не имеет смысла при x = -0,5. Поэтому единственный возможный корень исходного уравнения — это х = 2, удовлетворяющий всем условиям области определения. Поскольку, возводя обе части уравнения в квадрат, мы всякий раз соблюдали условие равносильности, то х = 2 — единственный корень исходного уравнения.Пример 34.Решим уравнение: 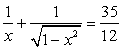 .При решении этого уравнения покажем применение метода введения новой переменной при решении иррациональных уравнений.Возведем обе части уравнения в квадрат:
.При решении этого уравнения покажем применение метода введения новой переменной при решении иррациональных уравнений.Возведем обе части уравнения в квадрат: 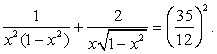 Пусть теперь
Пусть теперь 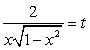 , тогда уравнение можно переписать в виде:
, тогда уравнение можно переписать в виде: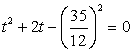 .Это уравнение имеет два корня:
.Это уравнение имеет два корня: 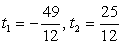 . Таким образом, следствием исходного уравнения является совокупность систем:
. Таким образом, следствием исходного уравнения является совокупность систем: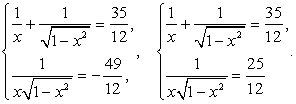 Решим первую систему совокупности.Обозначим:
Решим первую систему совокупности.Обозначим: 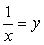 и
и 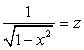 .Тогда имеем:
.Тогда имеем: 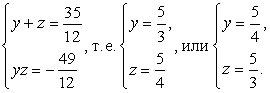 Таким образом,
Таким образом, 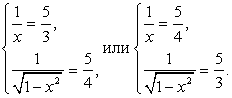 Корни этой совокупности систем:
Корни этой совокупности систем: 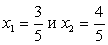 Аналогично, решая вторую систему исходной совокупности, получаем:
Аналогично, решая вторую систему исходной совокупности, получаем: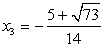 .Пример 35.Решим уравнение:
.Пример 35.Решим уравнение: 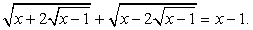 Подкоренные выражения
Подкоренные выражения 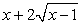 и
и 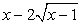 представляют из себя полные квадраты:
представляют из себя полные квадраты: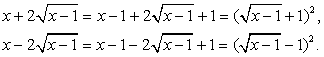 Тогда:
Тогда: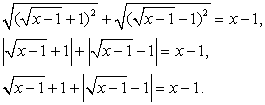 Пусть
Пусть 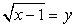 , тогда уравнение можно переписать в виде:
, тогда уравнение можно переписать в виде: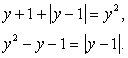 Возведем обе части последнего уравнения в квадрат, затем воспользуемся тождеством
Возведем обе части последнего уравнения в квадрат, затем воспользуемся тождеством 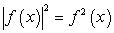 и формулой разности квадратов:
и формулой разности квадратов: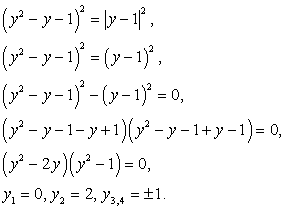 Если у = 0, то
Если у = 0, то 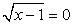 , т.е. х = 1. Если у = 2, то
, т.е. х = 1. Если у = 2, то 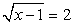 , т.е. х = 5. Если у = 1, то
, т.е. х = 5. Если у = 1, то 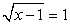 , т.е. х = 2. Если у = -1, то уравнение
, т.е. х = 2. Если у = -1, то уравнение 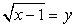 не имеет корней.Непосредственной подстановкой в исходное уравнение всех найденных значений х, приходим к выводу, что только х = 5 является корнем данного уравнения.Рассмотрим далее примеры решения иррациональных уравнений
не имеет корней.Непосредственной подстановкой в исходное уравнение всех найденных значений х, приходим к выводу, что только х = 5 является корнем данного уравнения.Рассмотрим далее примеры решения иррациональных уравнений с корнями степени, большей, чем вторая.Пример 36.Решим уравнение:
с корнями степени, большей, чем вторая.Пример 36.Решим уравнение: 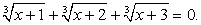 Перераспределим радикалы
Перераспределим радикалы 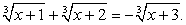 Возведем обе части уравнения в третью степень:
Возведем обе части уравнения в третью степень: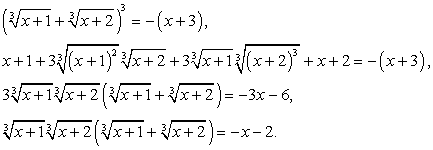 Выражение в скобках, очевидно, есть —
Выражение в скобках, очевидно, есть — 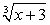 , т.е.:
, т.е.: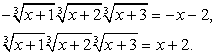 Снова возведем обе части уравнения в третью степень:
Снова возведем обе части уравнения в третью степень: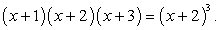 Далее имеем:
Далее имеем: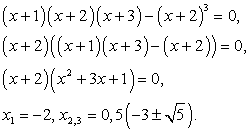 В процессе решения, был применен прием, связанный с заменой суммы
В процессе решения, был применен прием, связанный с заменой суммы 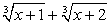 на выражение
на выражение 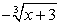 , что могло привести к появлению посторонних корней (такой вывод позволяет сделать определенная искусственность этого приема). Поэтому проверим все найденные корни непосредственной подстановкой в исходное уравнение.Если х = -2, то исходное уравнение обращается в верное числовое равенство.Для подстановки значений
, что могло привести к появлению посторонних корней (такой вывод позволяет сделать определенная искусственность этого приема). Поэтому проверим все найденные корни непосредственной подстановкой в исходное уравнение.Если х = -2, то исходное уравнение обращается в верное числовое равенство.Для подстановки значений 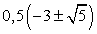 возьмем приближенное значение:
возьмем приближенное значение: 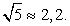 Тогда
Тогда 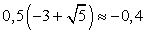 и
и 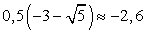 .Если х = -0,4, то:
.Если х = -0,4, то: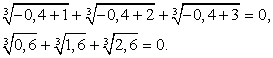 Ясно, что это числовое равенство неверно, поскольку все три значения корней положительны, а сумма положительных чисел не может быть равна 0.Если х = -2,6, то:
Ясно, что это числовое равенство неверно, поскольку все три значения корней положительны, а сумма положительных чисел не может быть равна 0.Если х = -2,6, то: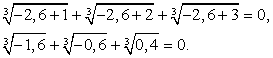 Ясно, что эта сумма не может быть равна 0, т.к. уже
Ясно, что эта сумма не может быть равна 0, т.к. уже 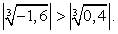 Заметим, что довольно часто, «прикидка» при проверки корней позволяет сделать необходимый вывод на определенном промежуточном этапе вычислений, и доводить их до явного числового равенства или неравенства совсем не обязательно (это снова к вопросу о гибкой тактике проверки корней).Таким образом, х = -2 — единственный корень данного уравнения.Ответ: -2.Комментарий. Запишем в общем виде прием решения, рассмотренный в этом примере:
Заметим, что довольно часто, «прикидка» при проверки корней позволяет сделать необходимый вывод на определенном промежуточном этапе вычислений, и доводить их до явного числового равенства или неравенства совсем не обязательно (это снова к вопросу о гибкой тактике проверки корней).Таким образом, х = -2 — единственный корень данного уравнения.Ответ: -2.Комментарий. Запишем в общем виде прием решения, рассмотренный в этом примере: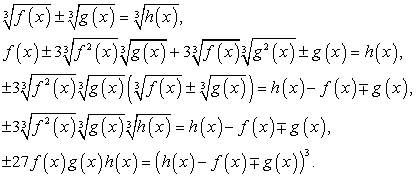 По аналогичной схеме решаются уравнения вида
По аналогичной схеме решаются уравнения вида 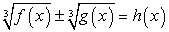 .Большие трудности у абитуриентов вызывают иррациональные уравнения
.Большие трудности у абитуриентов вызывают иррациональные уравнения , содержащие радикалы разных степеней. Рассмотрим примеры.Пример 37.
, содержащие радикалы разных степеней. Рассмотрим примеры.Пример 37.- а) Решим уравнение:
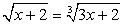 .Это уравнение легко рационализируется возведением обеих его частей в шестую степень:
.Это уравнение легко рационализируется возведением обеих его частей в шестую степень: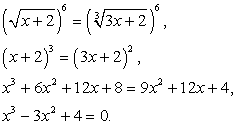 И далее:
И далее: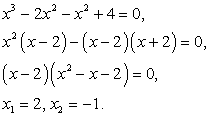 Подстановкой выясняем, что только х = 2 является корнем данного уравнения.б) Решим уравнение:
Подстановкой выясняем, что только х = 2 является корнем данного уравнения.б) Решим уравнение: 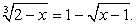 В этом случае возведение обеих частей уравнения в шестую степень уже нецелесообразно. Проведем замену переменных.Пусть
В этом случае возведение обеих частей уравнения в шестую степень уже нецелесообразно. Проведем замену переменных.Пусть 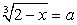 и
и 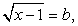 тогда a + b = 1. Возведем в куб первое уравнение системы
тогда a + b = 1. Возведем в куб первое уравнение системы 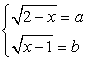 , и в квадрат второе уравнение этой системы; затем почленно сложим полученные уравнения. В итоге получаем: a3 + b2 = 1.Таким образом, имеем систему уравнений:
, и в квадрат второе уравнение этой системы; затем почленно сложим полученные уравнения. В итоге получаем: a3 + b2 = 1.Таким образом, имеем систему уравнений: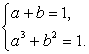 Решая ее, получаем:
Решая ее, получаем: 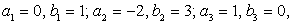 т.е. совокупность систем:
т.е. совокупность систем: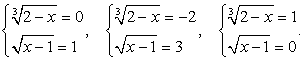 В итоге
В итоге 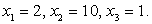 Непосредственная подстановка в исходное уравнение показывает, что среди этих корней нет посторонних.
Непосредственная подстановка в исходное уравнение показывает, что среди этих корней нет посторонних.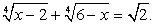 Пусть
Пусть 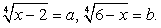 Тогда
Тогда 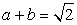 . Возведем в четвертую степень обе части каждого из уравнений системы
. Возведем в четвертую степень обе части каждого из уравнений системы 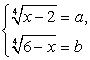 , и почленно сложим полученные уравнения. В итоге получаем:
, и почленно сложим полученные уравнения. В итоге получаем: 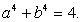 Таким образом, имеем систему уравнений:
Таким образом, имеем систему уравнений: 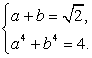 Это симметрическая система уравнений, стандартно решающаяся заменой переменных a + b = y и ab = z.Имеем корни:
Это симметрическая система уравнений, стандартно решающаяся заменой переменных a + b = y и ab = z.Имеем корни: 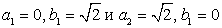 . Отсюда x1 = 2, x2 = 6. Проверка показывает, что это действительно корни данного уравнения.Ответ: x1 = 2, x2 = 6.Пример 39.Решим уравнение:
. Отсюда x1 = 2, x2 = 6. Проверка показывает, что это действительно корни данного уравнения.Ответ: x1 = 2, x2 = 6.Пример 39.Решим уравнение: 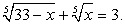 Аналогично предыдущему примеру получаем симметрическую систему относительно переменных
Аналогично предыдущему примеру получаем симметрическую систему относительно переменных 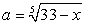 и
и 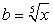 :
: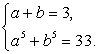 Корни этой системы легко угадываются:
Корни этой системы легко угадываются: 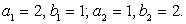 Далее получаем корни исходного уравнения: x1 = 1 и x2 = 32.Ответ: x1 = 1.Устойчивым является заблуждение абитуриентов о том, что при решении тригонометрических уравнений
Далее получаем корни исходного уравнения: x1 = 1 и x2 = 32.Ответ: x1 = 1.Устойчивым является заблуждение абитуриентов о том, что при решении тригонометрических уравнений не нужна проверка. Это — далеко не всегда.При решении тригонометрических уравнений проверка найденных решений необходима, если:
не нужна проверка. Это — далеко не всегда.При решении тригонометрических уравнений проверка найденных решений необходима, если:- 1) в процессе решения применялись алгебраические преобразования, которые могли привести к расширению области определения уравнения (например, сокращение дробей);2) в процессе решения применялись тригонометрические преобразования, которые могли привести к расширению области определения уравнения (речь идет о применении тригонометрических формул, левая и правая части которых имеют различные области определения, например:
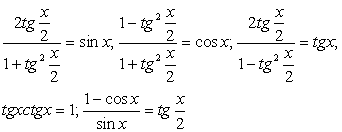 ;3) в процессе решения применялось возведение обеих частей уравнения в одну и ту же степень.
;3) в процессе решения применялось возведение обеих частей уравнения в одну и ту же степень.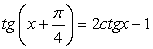 .Решение.Обе части уравнения легко представляются как выражение, зависящее только от tgx:
.Решение.Обе части уравнения легко представляются как выражение, зависящее только от tgx: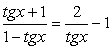 .Далее, заменой tgx = y, тригонометрическое уравнение рационализуется:
.Далее, заменой tgx = y, тригонометрическое уравнение рационализуется: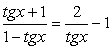 .В итоге
.В итоге 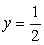 , т.е.
, т.е. 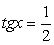 и
и 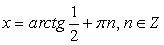 .Однако можно заметить, что значения
.Однако можно заметить, что значения 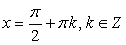 также удовлетворяют исходному уравнению. Это потерянные корни
также удовлетворяют исходному уравнению. Это потерянные корни . В чем причина?! В основе преобразований формулы, сужающие область определения:
. В чем причина?! В основе преобразований формулы, сужающие область определения: 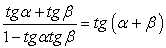 .(В нашем случае
.(В нашем случае 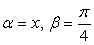 и
и 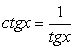 ).Еще раз настойчиво предостерегаем от применения приемов решения уравнений, ведущих к сужению области определения
).Еще раз настойчиво предостерегаем от применения приемов решения уравнений, ведущих к сужению области определения и возможной потере корней
и возможной потере корней .Пример 41.Решить уравнение:
.Пример 41.Решить уравнение: 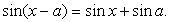 Решение.Перераспределим компоненты уравнения:
Решение.Перераспределим компоненты уравнения: 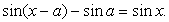 Далее, в левой части воспользуемся формулой:
Далее, в левой части воспользуемся формулой: 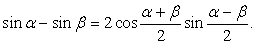 Имеем:
Имеем: 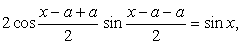 т.е.
т.е. 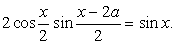 Теперь представим sin x как синус двойного аргумента:
Теперь представим sin x как синус двойного аргумента: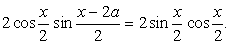 Перенесем все компоненты уравнения в одну часть и вынесем общий множитель за скобки:
Перенесем все компоненты уравнения в одну часть и вынесем общий множитель за скобки: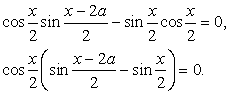 Вновь воспользуемся формулой разности синусов:
Вновь воспользуемся формулой разности синусов: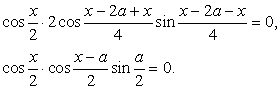 Последнее уравнение равносильно совокупности:
Последнее уравнение равносильно совокупности: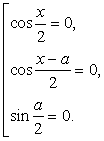 Таким образом, уравнение имеет два семейства корней:
Таким образом, уравнение имеет два семейства корней: 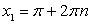 и
и 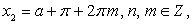 , если
, если 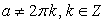 и бесконечно много корней:
и бесконечно много корней: 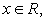 если
если 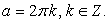 Ответ: если
Ответ: если 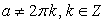 , то
, то 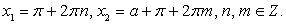 .если
.если 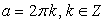 , то
, то 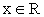 .Рассмотрим также примеры решения комбинированных уравнений
.Рассмотрим также примеры решения комбинированных уравнений , т.е. уравнений, в которых над переменной, в той или иной комбинации производятся иррациональные, показательно-степенные, логарифмические и тригонометрические операции. Такого рода задания вызывают у абитуриентов определенные трудности. В основе этих трудностей, как правило, лежит некая негативная психологическая установка. Абитуриент как бы говорит себе: «Таких уравнений я в школе не решал; что-то слишком много всего накручено; это мне не по силам». В связи с этим дадим два совета.Совет первый. По внешнему виду задания нельзя судить о его простоте или трудности; трудность — это характеристика не задания, а действенности Ваших знаний и умений. Начинайте решать, пробуйте, пытайтесь, несмотря на то, что задание кажется вам «страшным» и недоступным.Совет второй. Решайте комбинированное уравнение как бы по действиям, отграничивая иррациональную часть решения от логарифмической, логарифмическую от тригонометрической и т.п. Осуществить это можно введением новых переменных. В конце решения осуществляйте тем или иным образом проверку корней.Пример 42.Решить уравнение:
, т.е. уравнений, в которых над переменной, в той или иной комбинации производятся иррациональные, показательно-степенные, логарифмические и тригонометрические операции. Такого рода задания вызывают у абитуриентов определенные трудности. В основе этих трудностей, как правило, лежит некая негативная психологическая установка. Абитуриент как бы говорит себе: «Таких уравнений я в школе не решал; что-то слишком много всего накручено; это мне не по силам». В связи с этим дадим два совета.Совет первый. По внешнему виду задания нельзя судить о его простоте или трудности; трудность — это характеристика не задания, а действенности Ваших знаний и умений. Начинайте решать, пробуйте, пытайтесь, несмотря на то, что задание кажется вам «страшным» и недоступным.Совет второй. Решайте комбинированное уравнение как бы по действиям, отграничивая иррациональную часть решения от логарифмической, логарифмическую от тригонометрической и т.п. Осуществить это можно введением новых переменных. В конце решения осуществляйте тем или иным образом проверку корней.Пример 42.Решить уравнение: 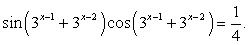 .Решение.Пусть
.Решение.Пусть 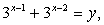 тогда
тогда 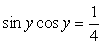 . Далее решаем уже не комбинированное, а тригонометрическое уравнение. Воспользуемся формулой синуса двойного аргумента:
. Далее решаем уже не комбинированное, а тригонометрическое уравнение. Воспользуемся формулой синуса двойного аргумента: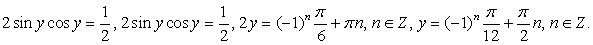 «Тригонометрическая часть» решения завершена; далее необходимо решить показательное уравнение с параметром n:
«Тригонометрическая часть» решения завершена; далее необходимо решить показательное уравнение с параметром n: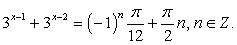 Прежде всего, выясним, при всех ли n у данного уравнения существуют корни. Ясно, что, поскольку левая часть уравнения, как сумма степеней тройки, всегда положительна, то условие существования корней уравнения:
Прежде всего, выясним, при всех ли n у данного уравнения существуют корни. Ясно, что, поскольку левая часть уравнения, как сумма степеней тройки, всегда положительна, то условие существования корней уравнения: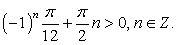 Решим это неравенство. Если n >
> 0, то
Решим это неравенство. Если n >
> 0, то 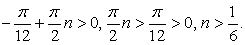 Очевидно, что полученная система
Очевидно, что полученная система 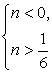 несовместна. Если n ≥
0, то
несовместна. Если n ≥
0, то 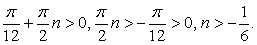 Система
Система 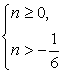 равносильна неравенству n ≥
0.Таким образом, учитывая, что
равносильна неравенству n ≥
0.Таким образом, учитывая, что 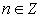 , получаем вывод: корни у данного уравнения существуют при значениях параметра n: n = 0, 1, 2, 3, …. Именно при этом условии решаем далее показательное уравнение.Преобразуем левую часть уравнения по свойствам степени:
, получаем вывод: корни у данного уравнения существуют при значениях параметра n: n = 0, 1, 2, 3, …. Именно при этом условии решаем далее показательное уравнение.Преобразуем левую часть уравнения по свойствам степени: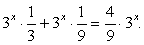 Тогда имеем:
Тогда имеем: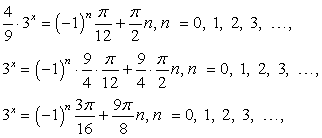 Таким образом,
Таким образом, 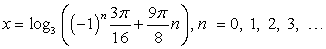 Это «семейство» логарифмов и составляет множество корней исходного комбинированного (показательно — тригонометрического) уравнения.Ответ:
Это «семейство» логарифмов и составляет множество корней исходного комбинированного (показательно — тригонометрического) уравнения.Ответ: 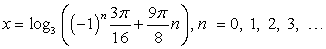 Пример 43.Решить уравнение:
Пример 43.Решить уравнение: 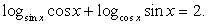 Решение.Прежде всего, укажем область определения уравнения. Она задается условиями:
Решение.Прежде всего, укажем область определения уравнения. Она задается условиями: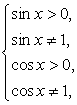 т.е. системой
т.е. системой 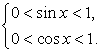 Пусть теперь
Пусть теперь 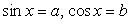 . Тогда, вместо комбинированного, имеем логарифмическое уравнение с двумя переменными а и b:
. Тогда, вместо комбинированного, имеем логарифмическое уравнение с двумя переменными а и b: 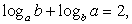 это уравнение преобразуется в уравнение:
это уравнение преобразуется в уравнение: 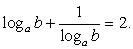 Далее, если положить, что
Далее, если положить, что 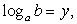 то имеем простое рациональное уравнение:
то имеем простое рациональное уравнение: 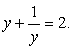 Его единственный корень — y = 1. Значит,
Его единственный корень — y = 1. Значит, 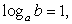 т.е.
т.е. 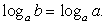 Отсюда b = a, т.е.
Отсюда b = a, т.е. 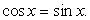 Корнями этого тригонометрического уравнения является семейство:
Корнями этого тригонометрического уравнения является семейство: 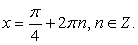 Нетрудно видеть, что оно удовлетворяет области определения исходного уравнения, а значит, и составляет множество его корней.Ответ:
Нетрудно видеть, что оно удовлетворяет области определения исходного уравнения, а значит, и составляет множество его корней.Ответ: 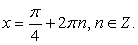 Пример 44.Решить уравнение:
Пример 44.Решить уравнение: 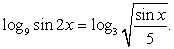 Решение.Заметим, что решение всякого уравнения следует начинать с пристального, внимательного взгляда, призванного увидеть в уравнении, неравенстве и т.п. что-нибудь интересное, особенное, какую-нибудь «изюминку», позволяющую применить при решении некий нестандартный прием. Эта «изюминка» не всегда есть, но проглядеть ее обидно. В данном уравнении маленькая «изюминка» есть: если в правой части уравнения мы воспользуемся (к сожалению часто забытым абитуриентами) свойством логарифма:
Решение.Заметим, что решение всякого уравнения следует начинать с пристального, внимательного взгляда, призванного увидеть в уравнении, неравенстве и т.п. что-нибудь интересное, особенное, какую-нибудь «изюминку», позволяющую применить при решении некий нестандартный прием. Эта «изюминка» не всегда есть, но проглядеть ее обидно. В данном уравнении маленькая «изюминка» есть: если в правой части уравнения мы воспользуемся (к сожалению часто забытым абитуриентами) свойством логарифма: 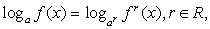 то сразу, как говорится, «убьем двух зайцев»: и избавимся от радикала, и перейдем к одному основанию логарифма.Итак, если r = 2, то
то сразу, как говорится, «убьем двух зайцев»: и избавимся от радикала, и перейдем к одному основанию логарифма.Итак, если r = 2, то 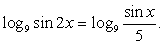 Далее, имеем тригонометрическое уравнение
Далее, имеем тригонометрическое уравнение 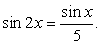 Воспользуемся формулой синуса двойного аргумента:
Воспользуемся формулой синуса двойного аргумента: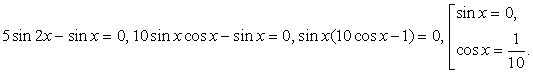 Решением первого уравнения совокупности является семейство:
Решением первого уравнения совокупности является семейство: 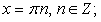 решением второго:
решением второго: 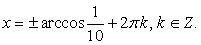 Необходимо провести проверку найденных корней. Для этого выпишем условия, задающие область определения исходного уравнения:
Необходимо провести проверку найденных корней. Для этого выпишем условия, задающие область определения исходного уравнения: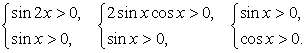 Ясно, что первое из найденных семейств — семейство посторонних корней, т.к. нарушено условие
Ясно, что первое из найденных семейств — семейство посторонних корней, т.к. нарушено условие 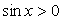 , а из второго семейства посторонними корнями являются корни вида:
, а из второго семейства посторонними корнями являются корни вида: 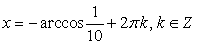 (т.к., в этом случае, хотя
(т.к., в этом случае, хотя 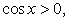 но
но 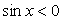 ).Таким образом, корни исходного комбинированного уравнения:
).Таким образом, корни исходного комбинированного уравнения: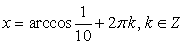 .Ответ:
.Ответ: 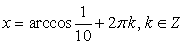 .Пример 45.Решить уравнение:
.Пример 45.Решить уравнение: 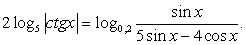 Решение.Внесем множитель два в левой части уравнения под логарифм в качестве показателя степени:
Решение.Внесем множитель два в левой части уравнения под логарифм в качестве показателя степени: 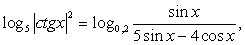 и перейдем к основанию логарифма пять в левой части уравнения:
и перейдем к основанию логарифма пять в левой части уравнения: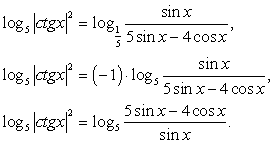 «Отбрасывая» логарифмы, получаем:
«Отбрасывая» логарифмы, получаем: 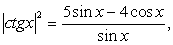 и далее, учитывая, что
и далее, учитывая, что 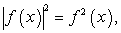 и переходя к разности дробей в левой части уравнения:
и переходя к разности дробей в левой части уравнения: 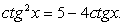 Это квадратное уравнение относительно ctg x, корни которого 1 и -5. Т.е. имеем совокупность:
Это квадратное уравнение относительно ctg x, корни которого 1 и -5. Т.е. имеем совокупность: 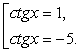 Решением первого уравнения совокупности является семейство:
Решением первого уравнения совокупности является семейство: 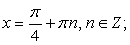 решением второго:
решением второго: 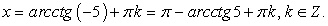 Здесь применено тождество:
Здесь применено тождество: 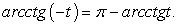 Далее необходимо провести проверку корней. В качестве способа проверки в данном случае, изберем непосредственную подстановку в исходное уравнение. При этом ясно, что речь идет о подстановке в исходное уравнение лишь одного значения принадлежащего данному семейству. Этого достаточно. Удобнее всего, взять значения n = 0 и х = -1. Но можно поступить еще проще: в равносильности совокупностей
Далее необходимо провести проверку корней. В качестве способа проверки в данном случае, изберем непосредственную подстановку в исходное уравнение. При этом ясно, что речь идет о подстановке в исходное уравнение лишь одного значения принадлежащего данному семейству. Этого достаточно. Удобнее всего, взять значения n = 0 и х = -1. Но можно поступить еще проще: в равносильности совокупностей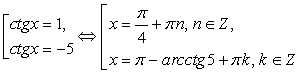 ,мы не сомневаемся, а поэтому в исходное уравнение можно подставлять непосредственно каждое из получившихся значений ctg x.В каждом случае изберем более удобный из описанных подходов.Пусть
,мы не сомневаемся, а поэтому в исходное уравнение можно подставлять непосредственно каждое из получившихся значений ctg x.В каждом случае изберем более удобный из описанных подходов.Пусть 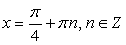 и n = 0, т.е.
и n = 0, т.е. 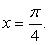 Тогда имеем:
Тогда имеем: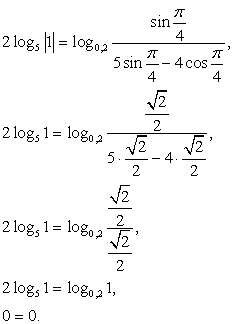 Таким образом, семейство:
Таким образом, семейство: 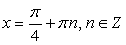 входит во множество корней исходного уравнения.Пусть теперь ctg x = -5 (здесь реализуем второй подход, ибо осуществлять непосредственную подстановку x = -arcctg 5 неудобно). Тогда, поскольку
входит во множество корней исходного уравнения.Пусть теперь ctg x = -5 (здесь реализуем второй подход, ибо осуществлять непосредственную подстановку x = -arcctg 5 неудобно). Тогда, поскольку 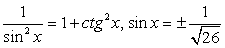 и
и 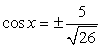 . Далее, т.к. ctg x <
0, то sin x и cos x должны быть разных знаков; имеем:
. Далее, т.к. ctg x <
0, то sin x и cos x должны быть разных знаков; имеем: 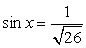 и
и 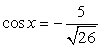 или
или 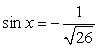 и
и 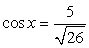 . В первом случае
. В первом случае 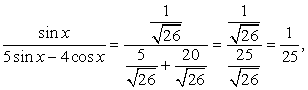 во втором случае
во втором случае 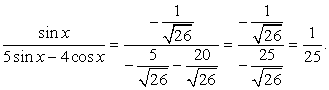 После подстановки в исходное уравнение имеем:
После подстановки в исходное уравнение имеем: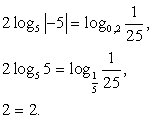 Таким образом, семейство
Таким образом, семейство 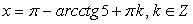 также входит во множество корней исходного уравнения.Ответ:
также входит во множество корней исходного уравнения.Ответ: 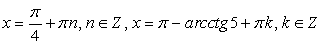 .Пример 46.Решить уравнение:
.Пример 46.Решить уравнение: 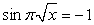 .Решение.
.Решение.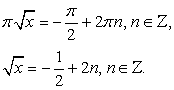 По определению арифметического квадратного корня
По определению арифметического квадратного корня перейдем к равносильной системе уравнений.
перейдем к равносильной системе уравнений.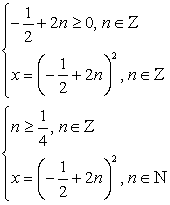 Ответ:
Ответ: 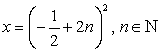 .Пример 47.Решить уравнение:
.Пример 47.Решить уравнение: 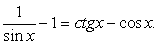 На первом этапе решения уравнения выясним область допустимых значений и выполним тождественные преобразования:
На первом этапе решения уравнения выясним область допустимых значений и выполним тождественные преобразования: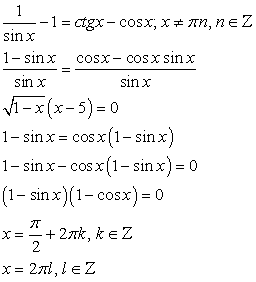 Решением уравнения является:
Решением уравнения является: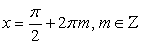 .Ответ:
.Ответ: 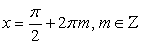 .Данный прием решения тригонометрического уравнения принято называть методом разложения на множители
.Данный прием решения тригонометрического уравнения принято называть методом разложения на множители .Пример 48.Решить уравнение:
.Пример 48.Решить уравнение: 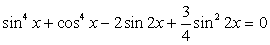 .Используем в процессе решения формулы понижения степени, получим:
.Используем в процессе решения формулы понижения степени, получим: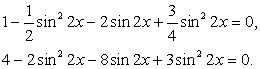 После приведения подобных слагаемых получаем уравнение, сводящееся к квадратному уравнению.
После приведения подобных слагаемых получаем уравнение, сводящееся к квадратному уравнению.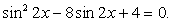 Данное уравнение приводится к квадратному с помощью замены переменной
Данное уравнение приводится к квадратному с помощью замены переменной .Пусть sin 2x = y, тогда:
.Пусть sin 2x = y, тогда: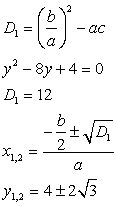
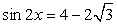 или
или 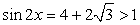
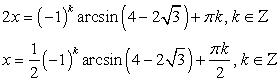 Ответ:
Ответ: 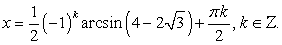 Решение большого количества тригонометрических уравнений сводится к решению квадратных уравнений
Решение большого количества тригонометрических уравнений сводится к решению квадратных уравнений .Пример 49.Решить уравнение:
.Пример 49.Решить уравнение: 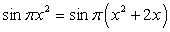 .
.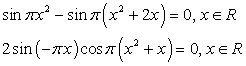
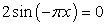 или
или 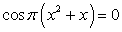
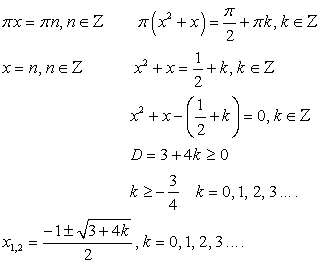 Ответ:
Ответ: 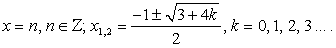 Данный пример иллюстрирует возможность решения тригонометрических уравнений методом преобразования суммы тригонометрических функций в произведение
Данный пример иллюстрирует возможность решения тригонометрических уравнений методом преобразования суммы тригонометрических функций в произведение .Пример 50.Решить уравнение:
.Пример 50.Решить уравнение: 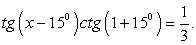 Во-первых, найдем область определения функции, выходящей в данной тригонометрическое уравнение:
Во-первых, найдем область определения функции, выходящей в данной тригонометрическое уравнение: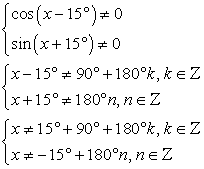 Таким образом, областью определения данного уравнения является:
Таким образом, областью определения данного уравнения является: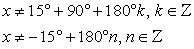 Во-вторых, решим данное уравнение. Для этого выполним следующие тождественные преобразования:
Во-вторых, решим данное уравнение. Для этого выполним следующие тождественные преобразования: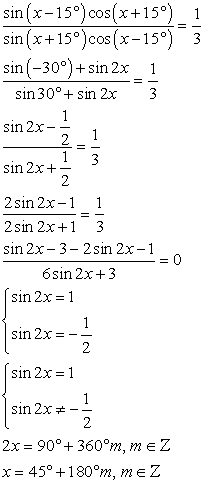 Ответ:
Ответ: 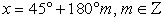 .Решение тригонометрических уравнений в ряде случаев проводится преобразованием произведения тригонометрических функций в сумму
.Решение тригонометрических уравнений в ряде случаев проводится преобразованием произведения тригонометрических функций в сумму .Пример 51.Решить тригонометрическое уравнение:
.Пример 51.Решить тригонометрическое уравнение: 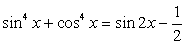 .Решение.Используем в процессе решения формулы понижения степени:
.Решение.Используем в процессе решения формулы понижения степени: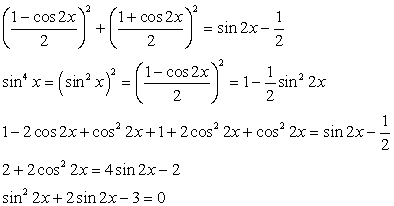 Выполнив замену переменных, получим:
Выполнив замену переменных, получим: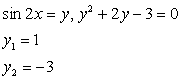
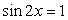 или
или 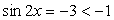
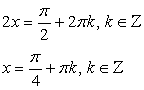 Ответ:
Ответ: 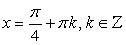 .Решение тригонометрических уравнений с применением формул понижения степени.Пример 52.Решить уравнение:
.Решение тригонометрических уравнений с применением формул понижения степени.Пример 52.Решить уравнение: 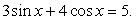 Решение.
Решение.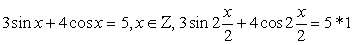 .Используем далее основное тригонометрическое тождество:
.Используем далее основное тригонометрическое тождество: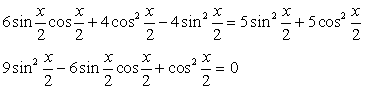 Если
Если 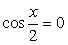 , то и
, то и 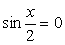 , что противоречит основному тригонометрическому тождеству, значит
, что противоречит основному тригонометрическому тождеству, значит 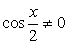 .Разделим обе части на
.Разделим обе части на 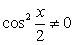 , получим:
, получим: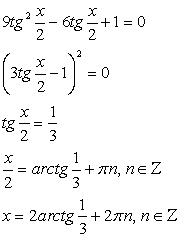 Ответ:
Ответ: 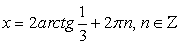 .Данный пример показывает возможность решения тригонометрических уравнений как однородных уравнений. Однородное уравнение
.Данный пример показывает возможность решения тригонометрических уравнений как однородных уравнений. Однородное уравнение — это уравнение, в котором каждое слагаемое имеет одну и ту же степень:
— это уравнение, в котором каждое слагаемое имеет одну и ту же степень: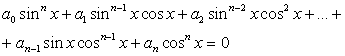 ,где
,где 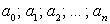 — действительные числа, n — показатель однородности.Пример 53.Решить уравнение:
— действительные числа, n — показатель однородности.Пример 53.Решить уравнение: 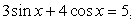 Решение.
Решение.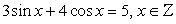 Т.к.
Т.к. 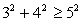 , следовательно, корни есть.Разделим обе части уравнения на
, следовательно, корни есть.Разделим обе части уравнения на 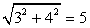 , получим:
, получим: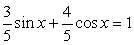 .Т.к.
.Т.к. 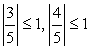 и
и 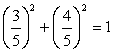 , то существует такой угол ?, что
, то существует такой угол ?, что 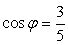 , а
, а 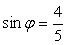 , тогда получим:
, тогда получим: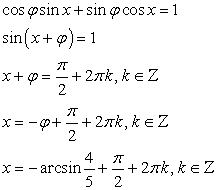 Ответ:
Ответ: 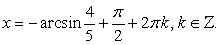 Рассмотренный прием решения тригонометрических уравнений называется методом введения вспомогательного аргумента
Рассмотренный прием решения тригонометрических уравнений называется методом введения вспомогательного аргумента .Данный метод основан на следующем. Рассмотрим уравнение особого вида:
.Данный метод основан на следующем. Рассмотрим уравнение особого вида: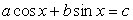 .Случай 1. Если с = 0, то уравнение однородное.Случай 2. Если с ≠
0 и
.Случай 1. Если с = 0, то уравнение однородное.Случай 2. Если с ≠
0 и 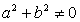 (то есть хотя бы одно из чисел a или b не равно 0), то разделим обе части уравнения на
(то есть хотя бы одно из чисел a или b не равно 0), то разделим обе части уравнения на 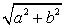 , получим:
, получим: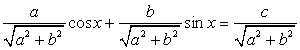 .Т.к.
.Т.к. 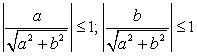 и
и 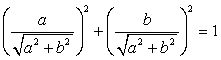 , то существует такой угол ?, что
, то существует такой угол ?, что 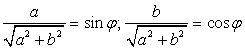 , тогда:
, тогда: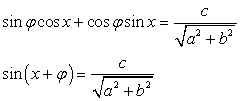 Пример 54.Решить уравнение:
Пример 54.Решить уравнение: 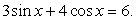 Решение.Проверим выполнение неравенства:
Решение.Проверим выполнение неравенства: 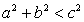 .Очевидно, что
.Очевидно, что 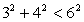 , следовательно, корней уравнение не имеет.Ответ:
, следовательно, корней уравнение не имеет.Ответ:  .Пример 55.Решить уравнение:
.Пример 55.Решить уравнение: 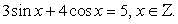 Выполним преобразование уравнения, используя формулы «универсальная тригонометрическая подстановка»
Выполним преобразование уравнения, используя формулы «универсальная тригонометрическая подстановка» :
: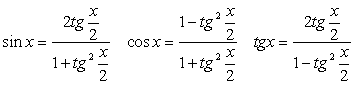 Получаем, что:
Получаем, что: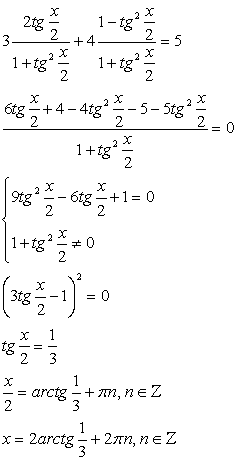 При переходе от уравнения (1) к уравнению (2), могла произойти потеря корней, значит необходимо проверить, являются ли корни уравнения
При переходе от уравнения (1) к уравнению (2), могла произойти потеря корней, значит необходимо проверить, являются ли корни уравнения 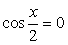 корнями данного уравнения.
корнями данного уравнения.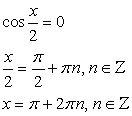 Проверка.Если
Проверка.Если 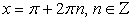 , тогда:
, тогда: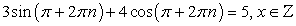 .0 + 4 (-1) = 5 — не верно, значит,
.0 + 4 (-1) = 5 — не верно, значит, 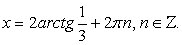 , не является корнями исходного уравнения.Ответ:
, не является корнями исходного уравнения.Ответ: 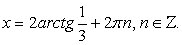 Данный пример показывает возможность решения тригонометрических уравнений с помощью универсальной тригонометрической подстановки.Пример 56.Решить уравнение:
Данный пример показывает возможность решения тригонометрических уравнений с помощью универсальной тригонометрической подстановки.Пример 56.Решить уравнение: 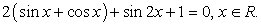 Решение.
Решение.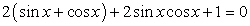 .Пусть
.Пусть 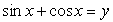 .Далее возведем записанное равенство в квадрат и воспользуемся формулой «квадрат суммы»:
.Далее возведем записанное равенство в квадрат и воспользуемся формулой «квадрат суммы»: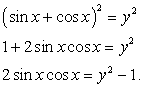 Получаем, что:
Получаем, что: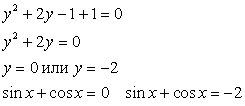 Разделим на cos x ≠
0, получим:
Разделим на cos x ≠
0, получим: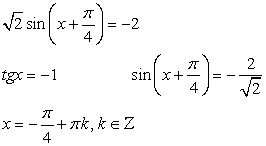 Т.к.
Т.к. 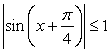 , при
, при 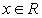 , то корней нет.Ответ:
, то корней нет.Ответ: 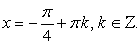 .Пример 57.Решить уравнение: 2cos 2x - 4sin x + 1 = 0.Решение.Используем формулу:
.Пример 57.Решить уравнение: 2cos 2x - 4sin x + 1 = 0.Решение.Используем формулу: 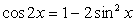 и сделаем замену
и сделаем замену 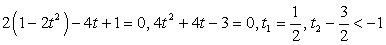 — посторонний корень (учитываем, что
— посторонний корень (учитываем, что 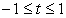 ).Выполним обратную замену:
).Выполним обратную замену: 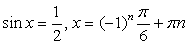 .Ответ:
.Ответ: 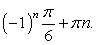 Пример 58.Решить уравнение:
Пример 58.Решить уравнение: 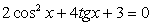 .Решение.Применим следствие из основного тождества
.Решение.Применим следствие из основного тождества 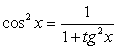 и сделаем замену t = tg x:
и сделаем замену t = tg x: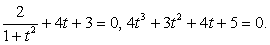 Найдем подбором корень t = -1 и разложим на множители левую часть полученного уравнения: (t + 1)(4t2 - t + 5) = 0. Дискриминант второго множителя отрицателен, следовательно, других корней уравнение не имеет. Обратная замена:
Найдем подбором корень t = -1 и разложим на множители левую часть полученного уравнения: (t + 1)(4t2 - t + 5) = 0. Дискриминант второго множителя отрицателен, следовательно, других корней уравнение не имеет. Обратная замена: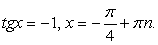 Ответ:
Ответ: 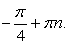 Приведенные приемы решения тригонометрических уравнений основаны на использовании основного тождества и формул для косинуса двойного угла.Пример 59.Решить уравнение:
Приведенные приемы решения тригонометрических уравнений основаны на использовании основного тождества и формул для косинуса двойного угла.Пример 59.Решить уравнение: 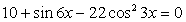 Поскольку
Поскольку 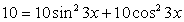 , a
, a 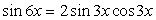 , уравнение можно записать в виде:
, уравнение можно записать в виде: 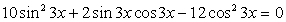 . Перед нами так называемое однородное уравнение, для всех слагаемых левой части которого сумма степеней sin 3x и cos 3x одинакова.Проверкой можно убедиться, что cos 3x ≠
0 для корней этого уравнения, поэтому можно разделить обе его части на
. Перед нами так называемое однородное уравнение, для всех слагаемых левой части которого сумма степеней sin 3x и cos 3x одинакова.Проверкой можно убедиться, что cos 3x ≠
0 для корней этого уравнения, поэтому можно разделить обе его части на 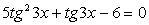 . Сделаем замену: t = tg 3x, тогда
. Сделаем замену: t = tg 3x, тогда 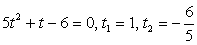 . Обратная замена:
. Обратная замена: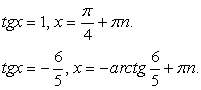 Ответ:
Ответ: 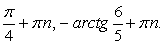 Пример 60.Решить уравнение: 5sin 4x - 12cos 4x = 6,5.Решение.
Пример 60.Решить уравнение: 5sin 4x - 12cos 4x = 6,5.Решение.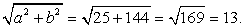 Разделим обе части уравнения на 13:
Разделим обе части уравнения на 13: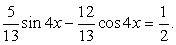 Пусть
Пусть  тогда
тогда 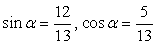 , и уравнение принимает вид:
, и уравнение принимает вид: 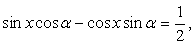 или
или 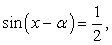 откуда
откуда 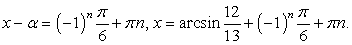 Ответ:
Ответ: 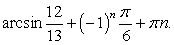 Пример 61.Решить уравнение: sin 4x + sin 3x + cos 6x + cos 7x = 0.Решение.Преобразуем в произведение сумму синусов и сумму косинусов:
Пример 61.Решить уравнение: sin 4x + sin 3x + cos 6x + cos 7x = 0.Решение.Преобразуем в произведение сумму синусов и сумму косинусов: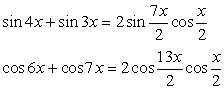 .Теперь запишем левую часть уравнения в виде:
.Теперь запишем левую часть уравнения в виде: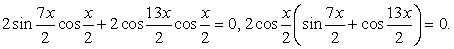 Это равенство возможно в двух случаях.Случай 1:
Это равенство возможно в двух случаях.Случай 1: 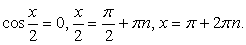 Случай 2:
Случай 2: 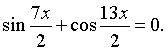 Применим формулу приведения:
Применим формулу приведения: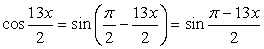 .Тогда:
.Тогда: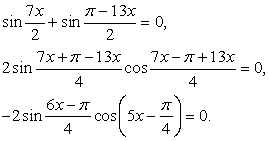 Это уравнение вновь сводится к двум простейшим:
Это уравнение вновь сводится к двум простейшим: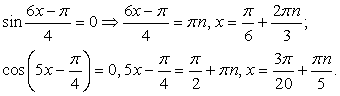 Ответ:
Ответ: 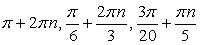 .Пример 62.Решить уравнение:
.Пример 62.Решить уравнение: 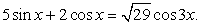 Решение.Применим к левой части метод дополнительного угла
Решение.Применим к левой части метод дополнительного угла :
: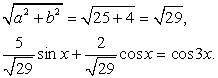 Выберем дополнительный угол так, чтобы получить в левой части формулу для косинуса разности:
Выберем дополнительный угол так, чтобы получить в левой части формулу для косинуса разности: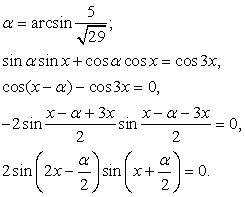 Случай 1:
Случай 1: 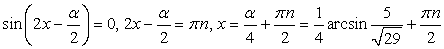 .Случай 2:
.Случай 2: 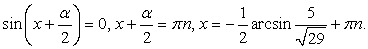 Ответ:
Ответ: 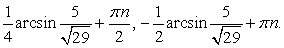 Решение примера основано на формуле преобразования суммы тригонометрических функций в произведение.Пример 63.Решить уравнение: cos 9x + sin 4x sin 5x = 0.Решение.Преобразуем произведение синусов в сумму:
Решение примера основано на формуле преобразования суммы тригонометрических функций в произведение.Пример 63.Решить уравнение: cos 9x + sin 4x sin 5x = 0.Решение.Преобразуем произведение синусов в сумму: 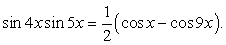 Тогда
Тогда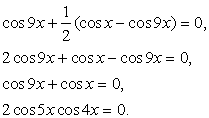 Случай 1:
Случай 1: 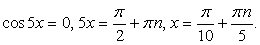 Случай 2:
Случай 2: 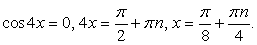 Ответ:
Ответ: 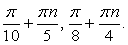 Пример 64.Решить уравнение: sin 6x + 3sin 4x cos 2x = 0.Решение.Преобразуем произведение в сумму:
Пример 64.Решить уравнение: sin 6x + 3sin 4x cos 2x = 0.Решение.Преобразуем произведение в сумму: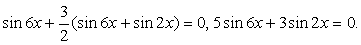 Воспользуемся формулой синуса тройного угла:
Воспользуемся формулой синуса тройного угла: 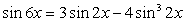 и сделаем замену: t = sin 2x. Решим уравнение для t:
и сделаем замену: t = sin 2x. Решим уравнение для t: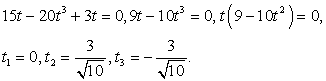 Обратная замена приводит к трем простейшим уравнениям.Случай 1:
Обратная замена приводит к трем простейшим уравнениям.Случай 1: 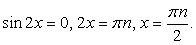 Случай 2:
Случай 2: 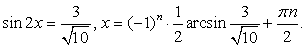 Случай 3:
Случай 3: 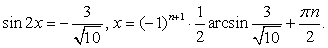 Объединяя две последние группы корней, получим окончательный ответ.Ответ:
Объединяя две последние группы корней, получим окончательный ответ.Ответ: 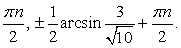 Рассмотренный пример иллюстрирует использование преобразования произведения тригонометрических функций в сумму.Пример 65.Решить уравнение: sin 2x - 5 + 5sin x - 5cos x = 0.Решение.Сделаем замену: t = sin x - cos x, тогда
Рассмотренный пример иллюстрирует использование преобразования произведения тригонометрических функций в сумму.Пример 65.Решить уравнение: sin 2x - 5 + 5sin x - 5cos x = 0.Решение.Сделаем замену: t = sin x - cos x, тогда 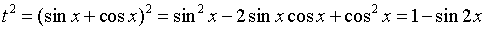 . Следовательно, sin 2x = 1 - t2.Подставим эти выражения в уравнение:1 - t2 - 5 + 5t = 0, t2 - 5t + 4 = 0, t1 = 1, t2 = 4.Очевидно, что разность синуса и косинуса не может равняться четырем, поскольку эти функции не принимают значений, модуль которых превышает 1; поэтому второй корень квадратного уравнения — посторонний. Для t = 1 сделаем обратную замену: sin x - cos x = 1. Применим метод дополнительного угла:
. Следовательно, sin 2x = 1 - t2.Подставим эти выражения в уравнение:1 - t2 - 5 + 5t = 0, t2 - 5t + 4 = 0, t1 = 1, t2 = 4.Очевидно, что разность синуса и косинуса не может равняться четырем, поскольку эти функции не принимают значений, модуль которых превышает 1; поэтому второй корень квадратного уравнения — посторонний. Для t = 1 сделаем обратную замену: sin x - cos x = 1. Применим метод дополнительного угла: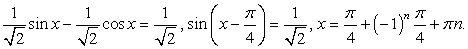 Ответ:
Ответ: 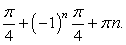 Пример 66.Решить уравнение:
Пример 66.Решить уравнение: 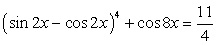 .Решение.Поскольку
.Решение.Поскольку 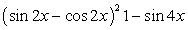 , представим
, представим 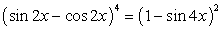 .Кроме того,
.Кроме того, 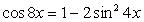 . Эти преобразования позволяют сделать замену: t = sin 4x и получить для t уравнение:
. Эти преобразования позволяют сделать замену: t = sin 4x и получить для t уравнение: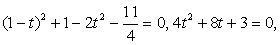
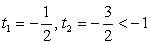 — посторонний корень.Сделаем обратную замену:
— посторонний корень.Сделаем обратную замену: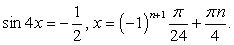 Ответ:
Ответ: 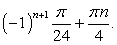 Данный пример предполагает использование тождеств:
Данный пример предполагает использование тождеств: 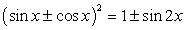 Решение следующих четырех примеров основано на формулах понижения степени
Решение следующих четырех примеров основано на формулах понижения степени . Напомним, что четные степени синуса и косинуса можно понизить переходом к двойному углу с помощью следующих формул:
. Напомним, что четные степени синуса и косинуса можно понизить переходом к двойному углу с помощью следующих формул: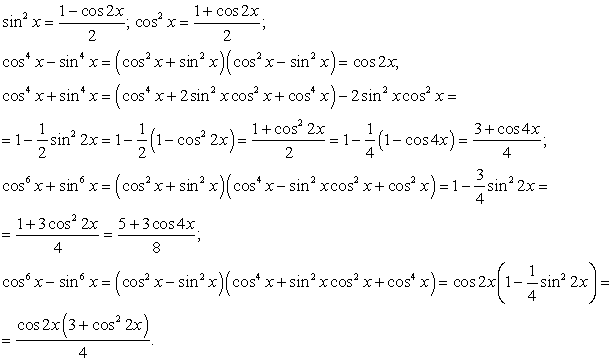 Пример 67.Решить уравнение:
Пример 67.Решить уравнение: 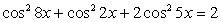 Решение.Понизим степени тригонометрических функций, входящих в уравнение:
Решение.Понизим степени тригонометрических функций, входящих в уравнение: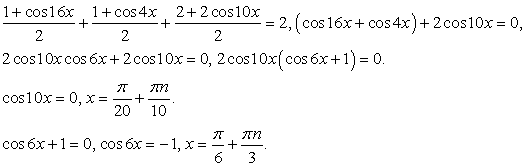 Ответ:
Ответ: 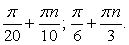 Пример 68.Решить уравнение:
Пример 68.Решить уравнение: 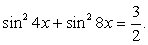 Решение.При понижении степени первого слагаемого оно выразится через cos 8x, поэтому у второго слагаемого мы не будем понижать степень, а вместо этого применим к нему основное тождество:
Решение.При понижении степени первого слагаемого оно выразится через cos 8x, поэтому у второго слагаемого мы не будем понижать степень, а вместо этого применим к нему основное тождество: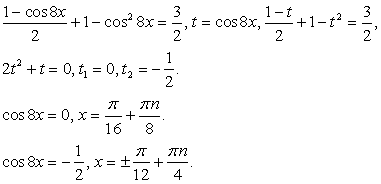 Ответ:
Ответ: 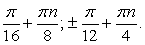 Пример 69.Решить уравнение:
Пример 69.Решить уравнение: 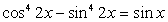 Решение.Преобразуем разность четвертых степеней: cos 4x = sin x и применим формулу приведения:
Решение.Преобразуем разность четвертых степеней: cos 4x = sin x и применим формулу приведения: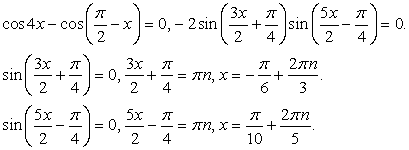 Ответ:
Ответ: 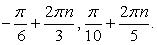 Пример 70.Решить уравнение:
Пример 70.Решить уравнение: 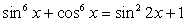 Решение.Выразим
Решение.Выразим 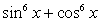 через
через 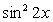 :
: 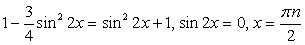 .Ответ:
.Ответ: 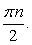 Пример 71.Решить уравнение:
Пример 71.Решить уравнение: 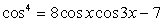 Решение.Понизим степень в левой части уравнения, а в правой преобразуем произведение в сумму:
Решение.Понизим степень в левой части уравнения, а в правой преобразуем произведение в сумму: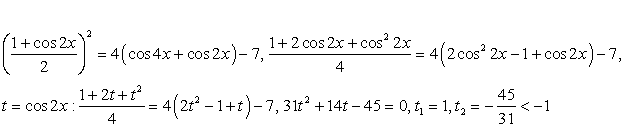
— посторонний корень.Обратная замена:
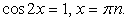 Ответ:
Ответ: 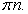 Пример 72.Решить уравнение: 20tg 8x + 15sin 8x + 2tg 4x = 0.Решение.Используем универсальную подстановку
Пример 72.Решить уравнение: 20tg 8x + 15sin 8x + 2tg 4x = 0.Решение.Используем универсальную подстановку :
: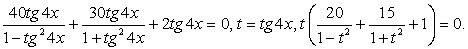 Случай 1:
Случай 1: 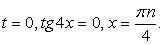 Случай 2:
Случай 2: 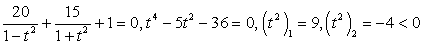 — постороннее решение.Тогда
— постороннее решение.Тогда 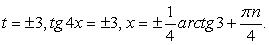 Ответ:
Ответ: 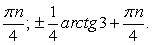 Пример 73.Решить уравнение:
Пример 73.Решить уравнение: 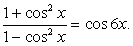 Решение.Обратим внимание на то, что левую часть уравнения с помощью одной из формул универсальной подстановки можно представить как:
Решение.Обратим внимание на то, что левую часть уравнения с помощью одной из формул универсальной подстановки можно представить как: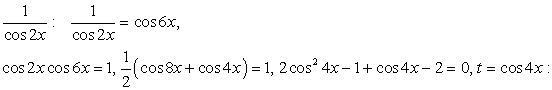
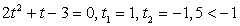 — посторонний корень.Обратная замена:
— посторонний корень.Обратная замена: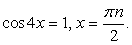 Ответ:
Ответ: 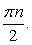 Уравнения, содержащие комбинации
Уравнения, содержащие комбинации 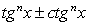 удобно решать, переходя к синусам и косинусам.Пример 74.Решить уравнение: 8sin 2x + 3 (tg x + ctg x) - 16 = 0.Решение.Преобразуем сумму тангенса и котангенса:
удобно решать, переходя к синусам и косинусам.Пример 74.Решить уравнение: 8sin 2x + 3 (tg x + ctg x) - 16 = 0.Решение.Преобразуем сумму тангенса и котангенса: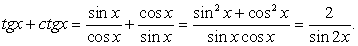 Теперь можно сделать замену:
Теперь можно сделать замену: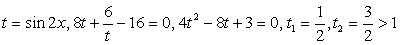 — посторонний корень.Обратная замена:
— посторонний корень.Обратная замена: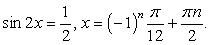 Ответ:
Ответ: 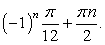 Пример 75.Решить уравнение:
Пример 75.Решить уравнение: 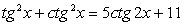 .Решение.Вновь выразим левую часть равенства через функции двойного угла:
.Решение.Вновь выразим левую часть равенства через функции двойного угла: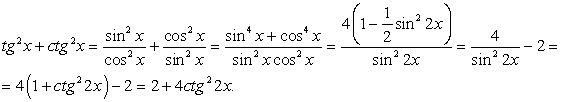 Теперь уравнение принимает вид:
Теперь уравнение принимает вид: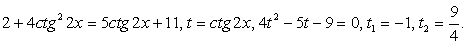 Случай 1:
Случай 1: 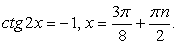 Случай 2:
Случай 2: 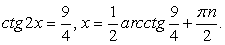 Ответ:
Ответ: 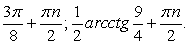 При решении тригонометрических уравнений (группа С) используются те же приемы, что и при решении алгебраических иррациональных уравнений. Особое внимание требуется обращать на дополнительные ограничения на допустимые значения неизвестного (самая распространенная ошибка в задачах этого типа — включение в ответ посторонних корней).Пример 76.Решить уравнение:
При решении тригонометрических уравнений (группа С) используются те же приемы, что и при решении алгебраических иррациональных уравнений. Особое внимание требуется обращать на дополнительные ограничения на допустимые значения неизвестного (самая распространенная ошибка в задачах этого типа — включение в ответ посторонних корней).Пример 76.Решить уравнение: 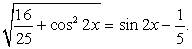 Решение.ОДЗ задается неравенством:
Решение.ОДЗ задается неравенством: 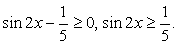 Возведем обе части в квадрат:
Возведем обе части в квадрат: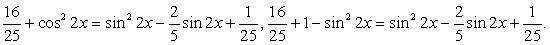 Замена
Замена 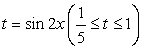 приводит к уравнению:
приводит к уравнению: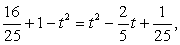
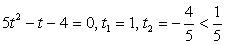 — посторонний корень.Обратная замена:
— посторонний корень.Обратная замена: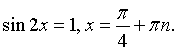 Ответ:
Ответ: 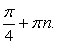 Пример 77.Решить уравнение:
Пример 77.Решить уравнение: 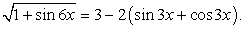 Решение.Обратим внимание на то, что подкоренное выражение представляет собой полный квадрат:
Решение.Обратим внимание на то, что подкоренное выражение представляет собой полный квадрат: 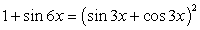 , следовательно,
, следовательно,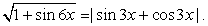 Сделаем замену: t = sin 3x + cos 3x, тогда |t| = 3 - 2t.Случай 1:
Сделаем замену: t = sin 3x + cos 3x, тогда |t| = 3 - 2t.Случай 1: 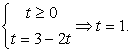 Случай 2:
Случай 2: 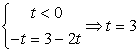 — посторонний корень (не соответствует условию раскрытия модуля).Итак,
— посторонний корень (не соответствует условию раскрытия модуля).Итак, 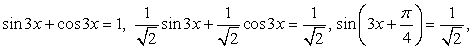
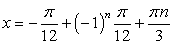 .Ответ:
.Ответ: 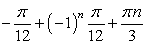 .Пример 78.Решить уравнение:
.Пример 78.Решить уравнение: 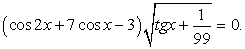 Решение.Ограничение на ОДЗ:
Решение.Ограничение на ОДЗ: 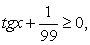 то есть
то есть 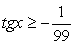 . Учитывая это условие, приравняем каждый множитель к нулю.Случай 1:
. Учитывая это условие, приравняем каждый множитель к нулю.Случай 1: 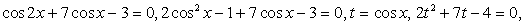
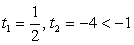 — посторонний корень.Следовательно,
— посторонний корень.Следовательно, 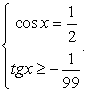 Этим условиям удовлетворяют углы вида
Этим условиям удовлетворяют углы вида 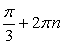 (вторая группа решений тригонометрического уравнения
(вторая группа решений тригонометрического уравнения 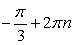 определяет углы, лежащие в четвертой четверти, тангенс которых равен
определяет углы, лежащие в четвертой четверти, тангенс которых равен 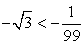 ).Случай 2:
).Случай 2: 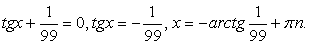 Ответ:
Ответ: 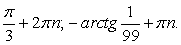 Для решения тригонометрических уравнений с модулями
Для решения тригонометрических уравнений с модулями применяются те же приемы, что и для алгебраических уравнений с модулями.Пример 79.Решить уравнение: sin 3x + |sin x| = 0.Решение.Во-первых,
применяются те же приемы, что и для алгебраических уравнений с модулями.Пример 79.Решить уравнение: sin 3x + |sin x| = 0.Решение.Во-первых, 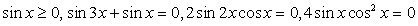 .Во-вторых,
.Во-вторых, 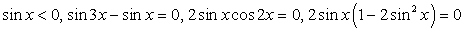 .Ответ:
.Ответ: 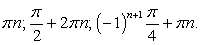 Пример 80.Решить уравнение: |sin 12x| + |sin 18x| = 0.Решение.Сумма модулей может равняться нулю только в том случае, если при одном и том же значении х оба подмодульных выражения равны нулю. Следовательно, нужно найти общие корни двух уравнений:
Пример 80.Решить уравнение: |sin 12x| + |sin 18x| = 0.Решение.Сумма модулей может равняться нулю только в том случае, если при одном и том же значении х оба подмодульных выражения равны нулю. Следовательно, нужно найти общие корни двух уравнений: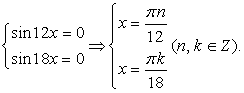 Принципиально важно то, что в решениях указаны разные целочисленные параметры
Принципиально важно то, что в решениях указаны разные целочисленные параметры . Для общих корней должно выполняться равенство
. Для общих корней должно выполняться равенство 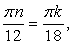 откуда
откуда 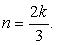 Поскольку n — целое число, дробь
Поскольку n — целое число, дробь 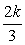 должна быть сократимой, а это возможно только если k кратно трем, то есть
должна быть сократимой, а это возможно только если k кратно трем, то есть 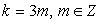 . Тогда решение уравнения можно записать так:
. Тогда решение уравнения можно записать так: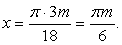 Ответ:
Ответ: 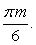 Рассмотрим далее тригонометрические уравнения с конечным числом корней
Рассмотрим далее тригонометрические уравнения с конечным числом корней . Эти уравнения очень необычны, и конечное число решений связано с тем, что аргумент тригонометрической функции принимает значения из некоторого конечного промежутка.Пример 81.Решить уравнение:
. Эти уравнения очень необычны, и конечное число решений связано с тем, что аргумент тригонометрической функции принимает значения из некоторого конечного промежутка.Пример 81.Решить уравнение: 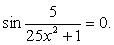 Решение.Найдем множество значений функции
Решение.Найдем множество значений функции 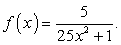 Очевидно, что
Очевидно, что 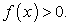 Исследуем ее на экстремум.
Исследуем ее на экстремум.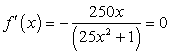 при х = 0 — найдена критическая точка.Слева от нее
при х = 0 — найдена критическая точка.Слева от нее 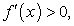 справа
справа 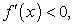 то есть это точка максимума. Так как он является единственным экстремумом, то при х = 0 функция принимает свое наибольшее значение: f (0) = 5.Следовательно,
то есть это точка максимума. Так как он является единственным экстремумом, то при х = 0 функция принимает свое наибольшее значение: f (0) = 5.Следовательно, 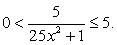 Решим простейшее тригонометрическое уравнение:
Решим простейшее тригонометрическое уравнение: 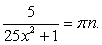 Из предыдущего исследования получаем, что равенство возможно только при условии
Из предыдущего исследования получаем, что равенство возможно только при условии 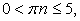 откуда
откуда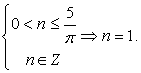 Действительно, это единственное целочисленное решение такого неравенства. Тогда
Действительно, это единственное целочисленное решение такого неравенства. Тогда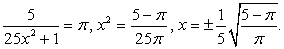 Ответ:
Ответ: 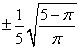 .В следующем примере рассмотрим комбинированные задачи
.В следующем примере рассмотрим комбинированные задачи , в которых применяются известные из алгебры методы решения систем и способы решения тригонометрических уравнений. Важно помнить, что при решении системы ответ каждого простейшего уравнения должен записываться с новым целочисленным параметром
, в которых применяются известные из алгебры методы решения систем и способы решения тригонометрических уравнений. Важно помнить, что при решении системы ответ каждого простейшего уравнения должен записываться с новым целочисленным параметром , который может принимать любое возможное значение независимо от ранее введенных параметров.Пример 82.Решить систему уравнений:
, который может принимать любое возможное значение независимо от ранее введенных параметров.Пример 82.Решить систему уравнений: 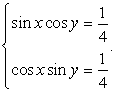 Решение.Применим метод алгебраического сложения
Решение.Применим метод алгебраического сложения : перейдем к системе, уравнениями которой будут сумма и разность исходных уравнений.
: перейдем к системе, уравнениями которой будут сумма и разность исходных уравнений.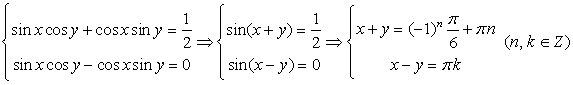 .Вновь сложим и вычтем полученные уравнения:
.Вновь сложим и вычтем полученные уравнения: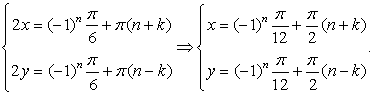 Ответ:
Ответ: 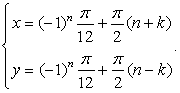 Пример 83.Решить систему уравнений:
Пример 83.Решить систему уравнений: 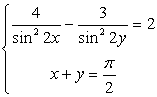 .Решение.Используем подстановку из второго уравнения:
.Решение.Используем подстановку из второго уравнения: 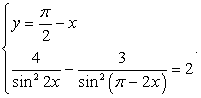 .Применим формулу приведения:
.Применим формулу приведения: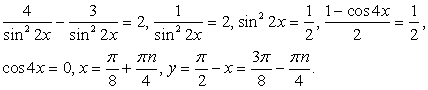 Ответ:
Ответ: 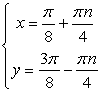 .Пример 84.Решить систему уравнений:
.Пример 84.Решить систему уравнений: 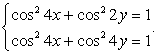 Решение.Вычтем первое уравнение из второго и применим формулу
Решение.Вычтем первое уравнение из второго и применим формулу 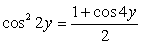 .
.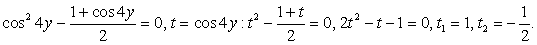 Случай 1: cos 4y = 1, тогда из второго уравнения
Случай 1: cos 4y = 1, тогда из второго уравнения 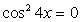 , то есть cos 4x = 0. Получена система двух простейших уравнений:
, то есть cos 4x = 0. Получена система двух простейших уравнений: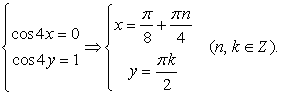 Случай 2:
Случай 2: 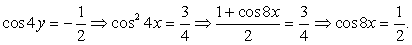 Решая полученную систему простейших уравнений, находим вторую группу корней:
Решая полученную систему простейших уравнений, находим вторую группу корней: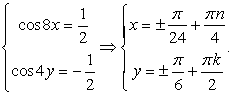 Еще раз напомним, что решение каждого уравнения системы содержит свой целочисленный параметр
Еще раз напомним, что решение каждого уравнения системы содержит свой целочисленный параметр (решением будет каждая пара чисел, заданная полученными формулами, в которых мы можем задавать n и k любые целые значения, не обязательно одинаковые).Ответ:
(решением будет каждая пара чисел, заданная полученными формулами, в которых мы можем задавать n и k любые целые значения, не обязательно одинаковые).Ответ: 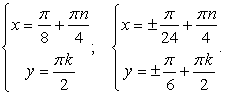 Видеолекция «Комбинированные уравнения»:
Видеолекция «Комбинированные уравнения»: 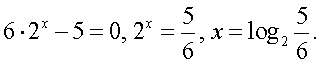
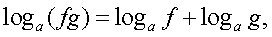
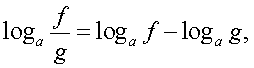
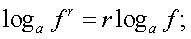
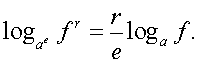
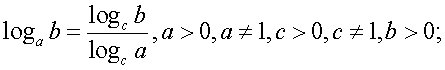
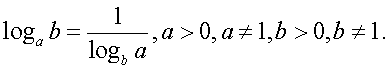
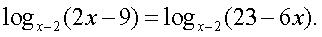
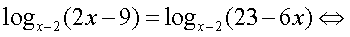
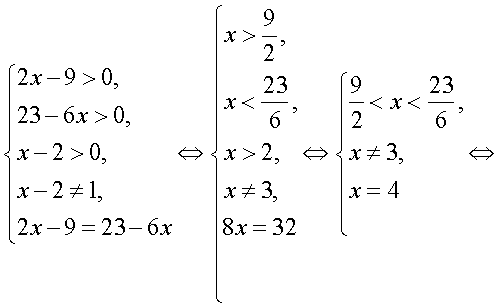 Ш.
Ш.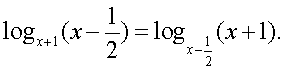
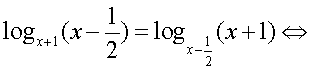
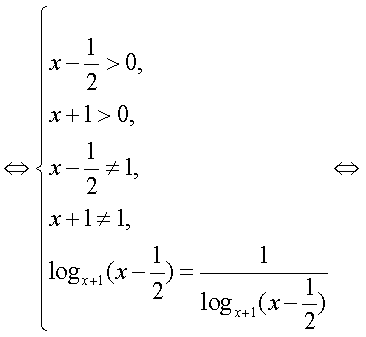
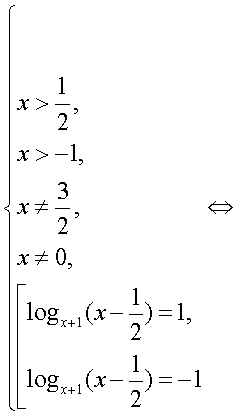
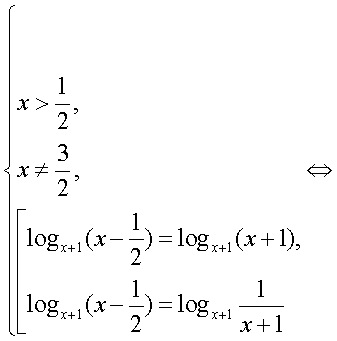
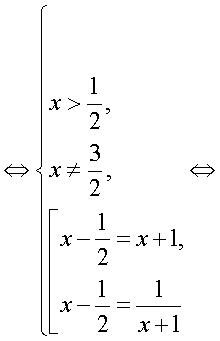
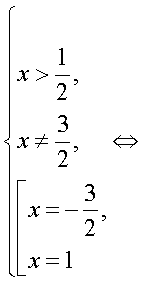
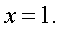
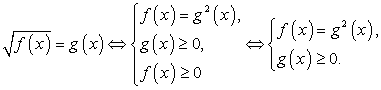
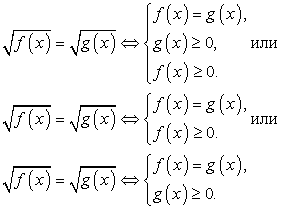
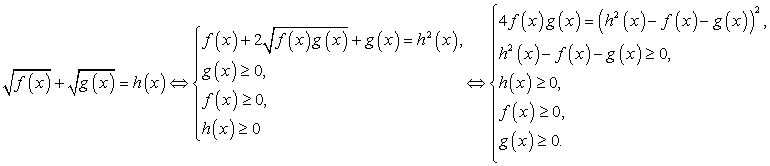
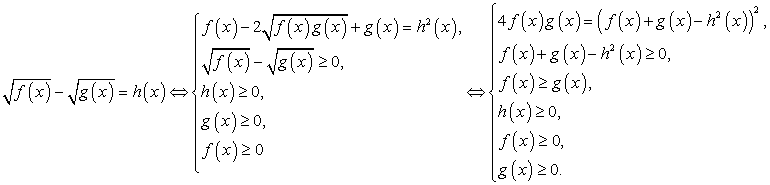
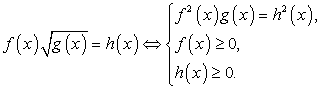
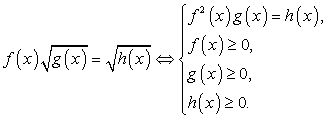
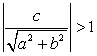 , т.е.
, т.е. 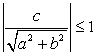 , т.е.
, т.е. 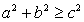 , тогда:
, тогда: