Прямые на плоскости и в пространстве. Плоскости в пространстве
- Две прямые в пространстве называются параллельными
, если они лежат в одной плоскости и не пересекаются. - Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися.
- Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну.
- Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.
- Признак параллельности прямой и плоскости:Если прямая, принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
- Две плоскости называются параллельными, если они не пересекаются.
- Признак параллельности плоскостей:Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
- Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, которая лежит в данной плоскости и проходит через точку пересечения.
- Признак перпендикулярности прямой и плоскости:Если прямая перпендикулярна двум пересекающимся прямым в плоскости, то она перпендикулярна данной плоскости.
- Теорема о трех перпендикулярах:Для того, чтобы прямая лежащая в плоскости, была перпендикулярна наклонной, необходимо и достаточно, чтобы эта прямая была перпендикулярна проекции наклонной.
- Если прямая, пересекающая плоскость, перпендикулярна двум прямым, лежащим в этой плоскости и проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.
- Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
- Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
- Если прямая, лежащая в плоскости, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной.
- Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, расположенной в этой плоскости, то она параллельна этой плоскости.
- Если прямая параллельна плоскости, то она параллельна некоторой прямой на этой плоскости.
- Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.
- Все точки прямой, параллельной плоскости, одинаково удалены от этой плоскости.
- Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых.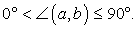
- Углом между двумя скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся.
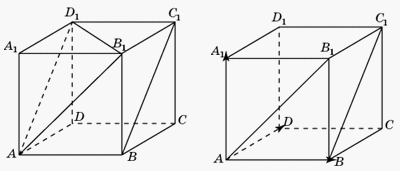
- 1-й способ. Прямая AD1 параллельна прямой BC1 и, следовательно, угол между прямыми AB1 и BC1 равен углу B1AD1. Треугольник B1AD1 равносторонний и, значит, угол B1AD1 равен
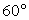.2-й способ. Введем систему координат, считая началом координат точку A, осями координат – прямые AB, AD, AA1.Вектор 
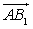имеет координаты (1, 0, 1). Вектор 
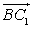имеет координаты (0, 1, 1). Воспользуемся формулой нахождения косинуса угла 
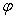между векторам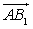и и 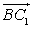. Получим 
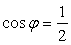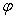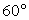и, значит, угол равен . Следовательно, искомый угол между прямыми AB1 и BC1 равен 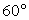..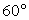Пример 2.В единичном кубе A…D1 найдите угол между прямыми DA1 и BD1.Решение.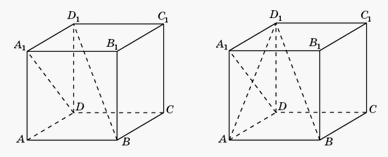
- 1-й способ. Рассмотрим ортогональную проекцию AD1 прямой BD1 на плоскость ADD1. Прямые AD1 и DA1 перпендикулярны. Из теоремы о трех перпендикулярах следует, что прямые DA1 и BD1 также перпендикулярны, т.е. искомый угол между прямыми DA1 и BD1 равен
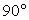.2-й способ. 
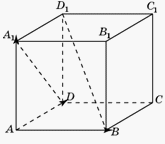Введем систему координат, считая началом координат точку A, осями координат – прямые AB, AD, AA1.Вектор 
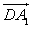имеет координаты (0, -1, 1). Вектор 
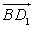имеет координаты (-1, 1, 1). Скалярное произведение этих векторов равно нулю и, значит, искомый угол между прямыми DA1 и BD1 равен 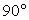..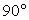Пример 3.В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите косинус угла между прямыми AD1 и CE1, где D1 и E1 – соответственно середины ребер A1C1 и B1C1.Решение.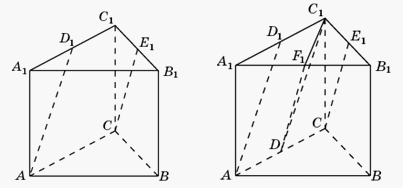
- 1-й способ. Обозначим D и F1 соответственно середины ребер AC и A1B1.DC1 || AD1 и DF1 || CE1, поэтому
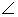(AD1;CE1) = C1DF1. 
C1DF1 равнобедренный,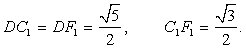
. Используя теорему косинусов, получаем cosC1DF1 = 0,7.2-й способ.Введем систему координат, считая началом координат точку A, как показано на рисунке.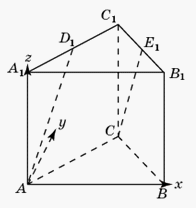 
Точка C имеет координаты 
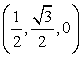, точка D1 имеет координаты 
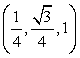, точка E1 имеет координаты 
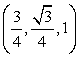. Вектор 
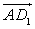имеет координаты 
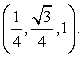Вектор 
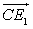имеет координаты 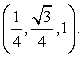Косинус угла между прямыми AD1 и CE1 равен косинусу угла между векторам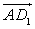и и 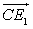. Воспользуемся формулой нахождения косинуса угла 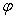между векторами. Получим cos 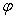= 0,7.- Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость.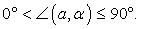
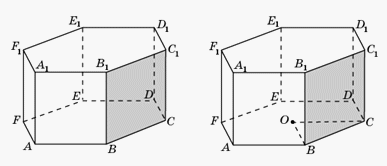Пусть O — центр нижнего основания призмы. Прямая BO параллельна AF. Так как плоскости ABC и BCC1 перпендикулярны, то искомым углом будет угол OBC. Так как треугольник OBC равносторонний, то этот угол будет равен 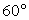.Ответ: 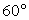.Пример 5.В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите угол между прямой CC1 и плоскостью BDE1.Решение.
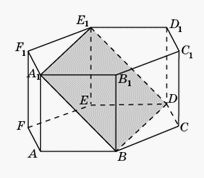Так как прямые BB1 и CC1 параллельны, то искомый угол будет равен углу между прямой BB1 и плоскостью BDE1. Прямая BD, через которую проходит плоскость BDE1, перпендикулярна плоскости ABB1 и, значит, плоскость BDE1 перпендикулярна плоскости ABB1. Следовательно, искомый угол будет равен углу A1BB1, т.е. равен 
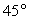.Ответ: 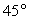.Пример 6.В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите синус угла между прямой BE и плоскостью SAD, где E — середина ребра SC.Решение.
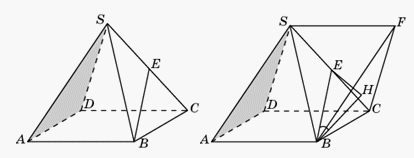Через вершину S проведем прямую, параллельную прямой AB, и отложим на ней отрезок SF, равный отрезку AB. В тетраэдре SBCF все ребра равны 1 и плоскость BCF параллельна плоскости SAD. Перпендикуляр EH, опущенный из точки E на плоскость BCF, равен половине высоты тетраэдра, т.е. равен 
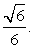Угол между прямой BE и плоскостью SAD равен углу EBH, синус которого равен 
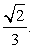.Ответ: 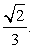Угол между двумя плоскостямиДвугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру.Величина двугранного угла принадлежит промежутку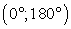 
.Величина угла между пересекающимися плоскостями принадлежит промежутку 
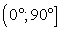.Построение линейного угла двугранного угла, образованного плоскостям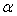и 
и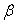 
: Строим два перпендикуляра 
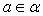и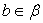 
к прямой пересечения плоскостей; а его величина находится из прямоугольного треугольника или из некоторого треугольника с применением теоремы косинусов: 
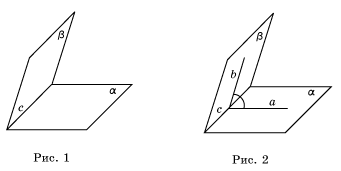Пример 7.В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите угол между плоскостями AFF1 и DEE1.Решение.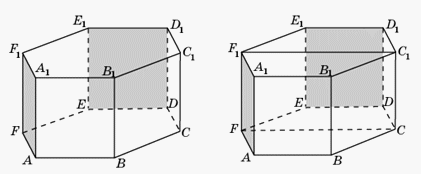
- 1-й способ. Так как плоскость FCC1параллельна плоскости DEE1, то искомый угол равен углу между плоскостями AFF1 и FCC1. Так как плоскости AFF1 и FCC1 перпендикулярны плоскости ABC, то соответствующим линейным углом будет угол AFC, который равен
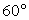.2-й способ. 
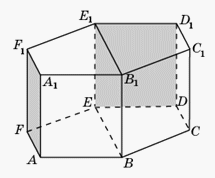Так как плоскость AFF1 параллельна плоскости BEE1, то искомый угол равен углу между плоскостями BEE1 и DEE1. Так как плоскости BEE1 и DEE1 перпендикулярны плоскости ABC, то соответствующим линейным углом будет угол BED, который равен 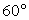..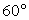Пример 8.В единичном кубе A…D1 найдите тангенс угла между плоскостями ADD1 и BDC1.Решение.
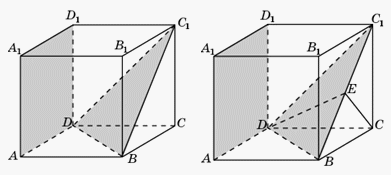Так как плоскость ADD1 параллельна плоскости BCC1, то искомый угол равен углу между плоскостями BCC1 и BDC1. Пусть E — середина отрезка BC1. Тогда прямые CE и DE будут перпендикулярны прямой BC1 и, следовательно, угол CED будет линейным углом между плоскостями BCC1 и BDC1. Треугольник CED прямоугольный, катет CD равен 1, катет CE равен 
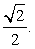Следовательно, tg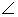CED =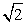
.Ответ: 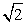.Пример 9.В правильной треугольной призме ABCA1B1C1D1, все ребра которой равны 1, найдите косинус угла между плоскостями ACB1 и BA1C1.Решение.
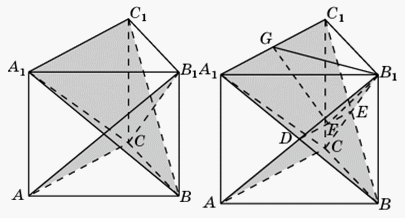Пусть DE — линия пересечения данных плоскостей, F — середина отрезка DE, G — середина отрезка A1C1. Угол GFB1 является линейным углом между данными плоскостями. В треугольнике GFB1 имеем:
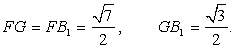По теореме косинусов находим 
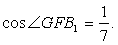Ответ: 1/7.Расстояние от точки до прямой- Расстояние от точки до прямой, не содержащей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую.
- Расстояние между двумя параллельными прямыми равно длине отрезка их общего перпендикуляра.
- Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой.
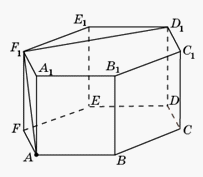Так как прямая D1F1 перпендикулярна плоскости AFF1, то отрезок AF1 будет искомым перпендикуляром, опущенным из точки A на прямую D1F1. Его длина равна 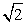.Ответ: 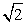.Пример 11.В единичном кубе A…D1 найдите расстояние от точки A до прямой BD1.Решение.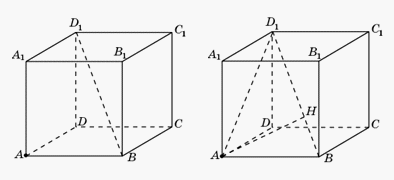
- 1-й способ. Искомым перпендикуляром является высота AH прямоугольного треугольника ABD1, в котором AB = 1, AD1 =
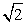, BD1 = 
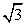. Для площади S этого треугольника имеют место равенства 
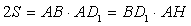.Откуда находим AH = 
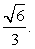2-й способ. Искомым перпендикуляром является высота AH прямоугольного треугольника ABD1, в котором AB = 1, AD1 = 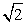, BD1 = 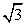. Треугольники BAD1 и BHA подобны по трем углам. Следовательно, AD1:BD1 = AH:AB.Откуда находим AH = 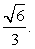3-й способ. Искомым перпендикуляром является высота AH прямоугольного треугольника ABD1, в котором AB=1, AD1= 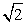, BD1= 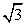.Откуда 
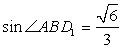и, следовательно,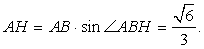 
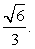Пример 12.В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2. Найти расстояние от точки F до прямой BG, где G — середина ребра SC.Решение.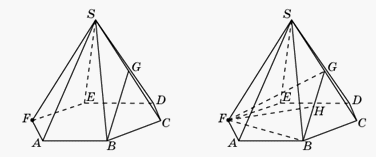
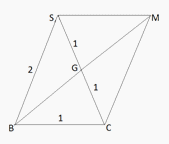Искомое расстояние от точки F до прямой BG равно высоте FH треугольника FBG, в котором по теореме косинусов в треугольнике AFB и по теореме Пифагора в треугольнике FSG: FB = FG = 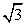. Найдем BG, как половину диагонали параллелограмма, который получим, если достроим треугольник BCG до параллелограмма CBSM, затем воспользуемся формулой: d12 + d22 = 2(a2 + b2 ).
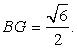По теореме Пифагора в треугольнике BFH находим FH:
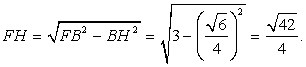Ответ: 
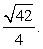Расстояние от точки до плоскости- Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость.
- Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.
- Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.
- Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра.
- Расстояние между двумя параллельными плоскостями равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.
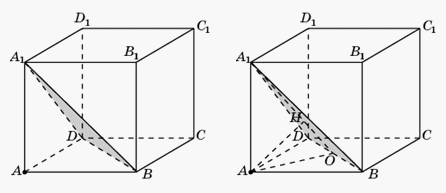
- 1-й способ. Пусть O — середина отрезка BD. Прямая BD перпендикулярна плоскости AOA1. Следовательно, плоскости BDA1 и AOA1 перпендикулярны. Искомым перпендикуляром, опущенным из точки A на плоскость BDA1, является высота AH прямоугольного треугольника AOA1, в котором AA1 = 1,
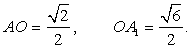Для площади S этого треугольника имеют место равенства 
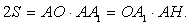Откуда находим AH = 
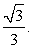2-й способ. Пусть O — середина отрезка BD. Прямая BD перпендикулярна плоскости AOA1. Следовательно, плоскости BDA1 и AOA1 перпендикулярны. Искомым перпендикуляром, опущенным из точки A на плоскость BDA1, является высота AH прямоугольного треугольника AOA1, в котором AA1 = 1,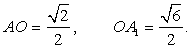Треугольники AOA1 и HOA подобны по трем углам. Следовательно, AA1 : OA1 = AH : AO.Откуда находим AH =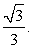3-й способ. Пусть O — середина отрезка BD. Прямая BD перпендикулярна плоскости AOA1. Следовательно, плоскости BDA1 и AOA1 перпендикулярны. Искомым перпендикуляром, опущенным из точки A на плоскость BDA1, является высота AH прямоугольного треугольника AOA1, в котором AA1 = 1,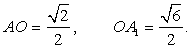Откуда 
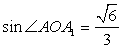и, следовательно,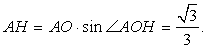 
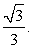Пример 14.В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние от точки A до плоскости SBC.Решение.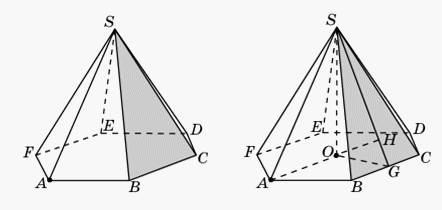
- 1-й способ. Пусть O — центр основания пирамиды. Прямая AO параллельна прямой BC и, значит, параллельна плоскости SBC. Следовательно, искомое расстояние равно расстоянию от точки O до плоскости SBC. Пусть G — середина отрезка BC. Тогда прямая OG перпендикулярна BC и искомым перпендикуляром, опущенным из точки O на плоскость SBC, является высота OH прямоугольного треугольника SOG. В этом треугольнике
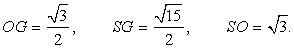Для площади S этого треугольника имеют место равенства 
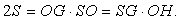Откуда находим OH = 
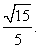.2-й способ. Пусть O — центр основания пирамиды. Прямая AO параллельна прямой BC и, значит, параллельна плоскости SBC. Следовательно, искомое расстояние равно расстоянию от точки O до плоскости SBC. Пусть G — середина отрезка BC. Тогда прямая OG перпендикулярна BC и искомым перпендикуляром, опущенным из точки O на плоскость SBC, является высота OH прямоугольного треугольника SOG. В этом треугольнике 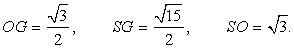Треугольники SOG и OHG подобны по трем углам. Следовательно, SO : SG = OH : OG. Откуда находим OH =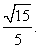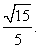Пример 15.В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние от точки A до плоскости BFE1.Решение.- 1-й способ.
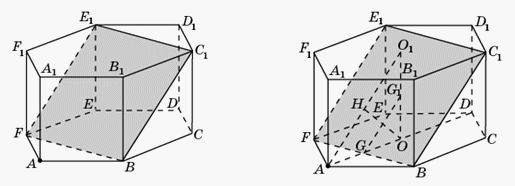Пусть O и O1 — центры оснований призмы. Прямая AO1 параллельна плоскости BFE1 и, следовательно, расстояние от точки A до плоскости BFE1 равно расстоянию от прямой AO1 до плоскости BFE1. Плоскость AOO1 перпендикулярна плоскости BFE1 и, следовательно, расстояние от прямой AO1 до плоскости BFE1 равно расстоянию от прямой AO1 до линии пересечения GG1 плоскостей AOO1 и BFE1. Треугольник AOO1 прямоугольный, AO = OO1 = 1, GG1 — его средняя линия. Следовательно, расстояние между прямыми AO1 и GG1 равно половине высоты OH треугольника AOO1, т.е. равно 
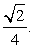2-й способ.
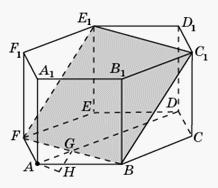Пусть G — точка пересечения прямых AD и BF. Угол между прямой AD и плоскостью BFE1 равен углу между прямыми BC и BC1 и равен 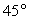. Перпендикуляр AH, опущенный из точки A на плоскость BFE1, равен 
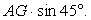Так как AG = 0,5, то AH =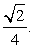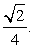Расстояние между скрещивающимися прямымиРасстояние между двумя скрещивающимися прямыми равно длине отрезка их общего перпендикуляра.Способы нахождения расстояния между скрещивающимися прямыми:- Найти длину общего перпендикуляра к этим прямым, если его можно построить
- Построить плоскость, содержащую одну из прямых и параллельную второй. Тогда искомое расстояние равно расстоянию от какой-нибудь точки второй прямой до построенной плоскости.
- Заключить данные прямые в параллельные плоскости, проходящие через данные скрещивающиеся прямые, и найти расстояние между этими плоскостями.
- Построить плоскость, перпендикулярную одной из данных прямых, и построить на этой плоскости ортогональную проекцию второй прямой:
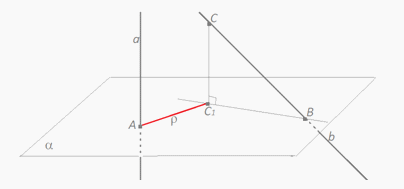
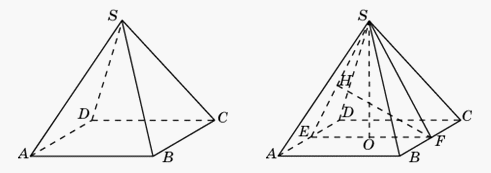Прямая BC параллельна плоскости SAD, в которой лежит прямая SA. Следовательно, расстояние между прямыми SA и BC равно расстоянию от прямой BC до плоскости SAD.Пусть E и F соответственно середины ребер AD и BC. Тогда искомым перпендикуляром будет высота FH треугольника SEF. В треугольнике SEF имеем: EF = 1, SE = SF =
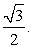, высота SO равна 
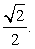Для площади S треугольника SEF имеют место равенства 
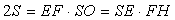, из которых получаем 
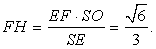Ответ: 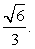Пример 17.В единичном кубе A…D1 найдите расстояние между прямыми AB1 и BC1.Решение.
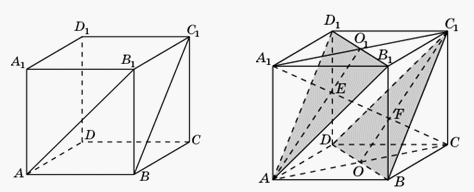Плоскости AB1D1 и BDC1, в которых лежат данные прямые, параллельны. Следовательно, расстояние между этими прямыми равно расстоянию между соответствующими плоскостями.Диагональ CA1 куба перпендикулярна этим плоскостям. Обозначим E и F точки пересечения диагонали CA1 соответственно с плоскостями AB1D1 и BDC1. Длина отрезка EF будет равна расстоянию между прямыми AB1 и BC1. Пусть O и O1 соответственно центры граней ABCD и A1B1C1D1 куба. В треугольнике ACE отрезок OF параллелен AE и проходит через середину AC. Следовательно, OF — средняя линия треугольника ACE и, значит, EF = FC. Аналогично доказывается, что O1E — средняя линия треугольника A1C1F и, значит, A1E = EF. Таким образом, 1 составляет одну треть диагонали CA1, т.е. EF =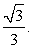Ответ: 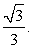Пример 18.В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние между прямыми AA1 и CF1.Решение.
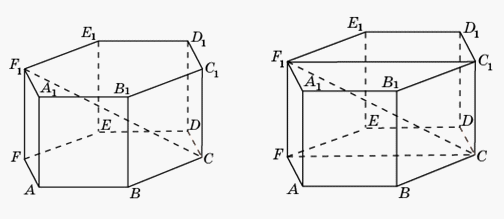Расстояние между прямыми AA1 и CF1 равно расстоянию между параллельными плоскостями ABB1 и CFF1, в которых лежат эти прямые. Оно равно 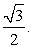Ответ: 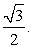Список используемой литературы Видеолекция «Прямые на плоскости и в пространстве. Плоскости в пространстве»: 
