Табличное и графическое представление данных
– самый простой способ упорядочить данные. С некоторыми таблицами вы уже имели дело. Это таблицы сложения и умножения чисел, таблицы спряжения глаголов. Таблицами являются: расписание уроков, страницы школьного дневника, оглавление учебника. Таблицы облегчают поиск необходимых сведений, не заставляя изучать всю имеющуюся информацию.Однако таблицы не дают наглядного представления о соотношении величин. Для этого служат различные диаграммы: столбиковые, круговые, рассеивания и др. Пословица гласит: «Лучше один раз увидеть». Диаграммы используются для наглядного, запоминающегося изображения и сопоставления данных.Таблицы и диаграммы удобно применять для сравнения шансов случайных событий, используя статистические данные (числовые данные, полученные в результате различных наблюдений, опросов, экспериментов.)На основе собранных статистических данных вычисляют частоту случайного события и выясняют, как она связана с вероятностью.Чтобы выяснить, насколько вероятно то или иное случайное событие, связанное со случайным экспериментом (эксперимент, условиями которого являются непредсказуемость и возможность многократного повторения), нужно подсчитать, как часто оно происходит. Для этого используют две важные величины – абсолютную и относительную частоту.Абсолютная частота показывает, сколько раз в серии экспериментов наблюдалось данное событие. Это всегда целое число.Относительная частота (частота 
) показывает, какая доля экспериментов завершилась наступлением данного события. Она равна отношению n - числа опытов, в которых интересующее нас событие произошло, к N - общему числу проведенных опытов. Это дробное число, меняющееся от 0 до 1.Опытным путем установлено, что проводя эксперименты огромное количество раз (больше 1000), например, такие эксперименты, как бросание игральной кости, бросание монеты, раздача игральных карт, розыгрыш лотереи и др., частоты становятся устойчивыми. Например, изобразим график зависимости частоты от числа опытов при бросании игральной кости, показывающий как часто выпадала «единица»: 
Другой пример. Событие А – «на кубике выпало четное число очков», событие В – «на кубике выпало нечетное число очков».
Устойчивость частот является скорее математическим, а не экспериментальным фактом. На нем основывается частотное, или статистическое определение вероятности: за вероятность случайного события можно приближенно принять его относительную частоту.В теории вероятностей величина, значение которой зависит от исхода эксперимента, называется случайной величиной. Мы будем рассматривать ряд числовых значений такой величины, полученных в какой-либо серии экспериментов. Такой числовой ряд называется случайной выборкой.Представим себе, что из всех школьников вашего региона случайным образом выбирается 1000 человек и фиксируется их оценка по математике в последней четверти. В статистике множество всех школьников региона будет называться генеральной совокупностью, а случайно выбранная 1000 школьников — случайной выборкой. Однако математики предпочитают иметь дело не со школьниками, а с числами, поэтому мы с вами будем называть случайной выборкой только числовой ряд — т. е. в нашем случае не самих выбранных школьников, а их оценки.Займемся числовыми рядами, полученными в результате описанной процедуры.Пример 1. Среди школьников седьмых классов был проведен выборочный опрос: из скольких человек состоят их семьи? В результате такого опроса была получена следующая выборка:223333423323232324322324523324323432 3 5 3Здесь каждое число означает количество человек в семье соответствующего ученика. Числа выписаны в том порядке, в котором ученики сдавали свои ответы. А что если упорядочить эти числа по возрастанию? 22222222222222 3333333333333333333 444 4 4 5 5Не правда ли, этот ряд (он называется ранжированным) воспринимается уже лучше: теперь мы ясно видим, что минимальное значение в нем равно 2, а максимальное — 5. Видно, как часто повторяется каждое из значений.А вот как выглядит представление выборки в виде частотной таблицы:
Состав семьи |
Абсолютная частота |
Относительная частота |
2 |
14 |
0,35 |
3 |
19 |
0,475 |
4 |
5 |
0,125 |
5 |
2 |
0,05 |
(т. е. количеству опрошенных учеников — 40), а сумма относительных — 1.Еще более наглядной формой представления результатов выборки является их графическое изображение. Для этого используется так называемый полигон частот — линейная диаграмма, на которой по горизонтальной оси откладываются различные значения, полученные в выборке, а по вертикальной — их относительная частота. После этого полученные точки соединяются ломаной линией (отсюда и название — полигон в переводе с греческого означает многоугольник).
Пример 2.На школьниках 1 «А» класса было проведено исследование для выяснения того, сколько весит портфель первоклассника. В результате взвешиваний был получен следующий числовой ряд (вес каждого портфеля в кг):2,1; 2,45; 1,9; 2,6; 3,1; 1,95; 3,4; 4,3; 1,15; 2,7;2,2; 3,2; 2,4; 2,2; 1,8; 1,5; 2,4; 2,25; 2,6; 1,75.Чем принципиально отличаются результаты этой выборки от примера 1? Чтобы ответить на этот вопрос, попробуем составить для нее таблицу частот:
Вес портфеля |
Абсолютная частота |
Относительная частота |
1,15 |
1 |
0,05 |
1,5 |
1 |
0,05 |
1,75 |
1 |
0,05 |
1,8 |
1 |
0,05 |
1,9 |
1 |
0,05 |
1,95 |
1 |
0,05 |
2,1 |
1 |
0,05 |
2,2 |
2 |
0,05 |
2,25 |
1 |
0,05 |
2,4 |
2 |
0,1 |
2,45 |
1 |
0,05 |
2,6 |
2 |
0,1 |
2,7 |
1 |
0,05 |
3,1 |
1 |
0,05 |
3,2 |
1 |
0,05 |
3,4 |
1 |
0,05 |
4,3 |
1 |
0,05 |
: весь диапазон значений выборки разбивают на интервалы (чаще всего равные) и подсчитывают частоту попадания в каждый интервал. Вот как будет выглядеть такая таблица в нашем примере, если разбить диапазон от 1 до 5 кг на четыре равных интервала:
Вес портфеля |
Абсолютная |
Относительная |
от 1 до 2 |
6 |
0,3 |
от 2 до 3 |
10 |
0,5 |
от 3 до 4 |
3 |
0,15 |
от 4 до 5 |
1 |
0,05 |
: по горизонтальной оси откладываются интервалы значений, а над каждым интервалом строится столбик, площадь которого равна относительной частоте попадания в данный интервал. Обратите внимание: именно площадь, а не высота. Хотя, если интервалы равные, то высоты всех столбиков отличаются от соответствующих частот только постоянным множителем — длиной интервала.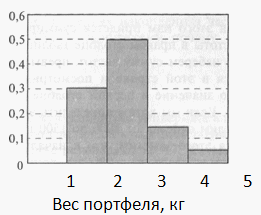
В некоторых задачах таблицу частот удобно дополнить еще одной характеристикой, получившей название накопленной частоты. Рассмотрим ее использование на примере.Пример 3. Перед вами еще одна интервальная таблица частот — распределение семей по уровню доходов:
Доход на человека |
Относительная |
менее 500 |
2% |
от 500 до 1000 |
6% |
от 1000 до 1500 |
7% |
от 1500 до 2000 |
12% |
от 2000 до 2500 |
36% |
от 2500 до 3000 |
27% |
свыше 3000 |
10% |
1285 рублей — это и есть та самая черта, которую диктор назвал «уровнем бедности».Решая эту задачу, мы должны были производить накопительное суммирование относительных частот до тех пор, пока не будет достигнут заданный уровень — 12%. Поскольку эти результаты можно использовать и для решения других задач, удобно хранить полученные результаты — накопленные частоты — в отдельном столбце таблицы:
Доход на |
Относительная частота |
Накопительная частота |
менее 500 |
2% |
2% |
от 500 до 1000 |
6% |
8% |
от 1000 до 1500 |
7% |
15% |
от 1500 до 2000 |
12% |
27% |
от 2000 до 2500 |
36% |
63% |
от 2500 до 3000 |
27% |
90% |
свыше 3000 |
10% |
100% |
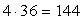человека имеют такой же доход.Ответ: 144.Список используемой литературы Видеолекция «Табличное и графическое представление данных»: 
