Задачи на работу и производительность
В определенном смысле задачи на работу схожи с задачам на движение. Сравните формулы: S = vt, V = vt. Роль скорости v здесь играет производительность труда, а роль расстояния S — объем работы V.Задачи на совместную работуДля понимания схемы решения задач на совместную работу, рассмотрим упрощенную модель.Пример 1.Вася с Колей мастерят из бумаги кораблики. Вася может сделать за 1 час 15 корабликов, а Коля только 10. Сколько времени им потребуется на 100 корабликов?Решение:За 1 час мальчики делают 15 + 10 = 25 корабликов. Значит, 100 корабликов они сделают за 100 : 25 = 4 часа.Итак, если дан общий объем работы и производительности труда «участников» задачи, то время совместной работы находят, разделив объем работы на совместную производительность труда: . (1)Пример 2.Вася выполняет свою работу за 2 часа, а Коля — за 3 часа. Сколько времени они потратят, если будут делать эту работу вдвоем?Решение:Скорость работы каждого из мальчиков: подставим в формулу (1): или .Поэтому, когда в задаче объем работы в явном виде не задан, его иногда удобно принять равным единице.В нашей задаче (ч).Иногда в задачах на совместную работу можно обойтись без решения уравнений, используя только арифметический способ. Правда, для этого порой приходится прибегать к гипотетическим допущениям. Рассмотрим такой пример.Пример 3.Маша и Даша за день могут прополоть 3 грядки, Даша и Глаша — 4 грядки, а Глаша и Маша — 5 грядок. Спрашивается, сколько грядок за день смогут прополоть девочки, работая втроем?Решение:Вообразим, что сначала Маша и Даша работали один день, затем Даша и Глаша работали один день, а потом Глаша и Маша работали еще один день. Получается, что каждая из девочек работала два дня или что бригада, состоящая из Маши, Глаши и Даши, прополола 3 + 4 + 5 = 12 грядок за два дня. Значит, за один день эта бригада прополет вдвое меньше грядок, т.е. 6.Эту же задачу можно решить «нашим» способом, с помощью уравнений.Обозначим и подставим в систему:Тогда втроем они выполнят работу за .Из последнего уравнения видим, что единица объема работы равна 6.Ответ: 6.Пример 4.Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?Решение:Составим для удобства таблицу:

 

V
(объем работы)

v
(производительность)

t
(время работы)

1-й рабочий

V

15

2-й рабочий

V

15

1-й рабочий

3

Вместе

Учитывая, что 1-й рабочий проработал 3 часа, а вместе работу доделали за 6 часов. Общее время работы 3 + 6 = 9 часов.Ответ: 9.Задачи на бассейныИногда в задачах на работу выделяют группу задач на трубы и бассейны, решение которых, вообще говоря, не имеет никаких специфических черт по сравнению с другими задачами на совместную работу. Математическая модель остается той же. Только рабочим будут соответствовать насосы разной производительности, а объему работы — объем бассейна или иного резервуара.Пример 5.Первая труба пропускает 15 литров воды в минуту, а вторая — 10. За сколько минут обе трубы наполнят бассейн, объемом 100 литров?Решение:Через 1 минуту из 1-й трубы нальется 15 литров, а из второй — 10. Значит, за минуту обе трубы наливают 15 + 10 = 25 литров. Тогда бассейн в 100 литров они наполнят за время 100 : 25 = 4 минуты.Итак, если дан объем резервуара и производительности работы труб (насосов), то время их совместной работы находят, разделив объем резервуара на совместную производительность труб:.Если в задаче объем резервуара в явном виде не задан, его иногда удобно принять равным единице: или .Пример 6.Первая труба пропускает на 6 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если бак, объемом 360 литров она заполняет на 10 минут медленнее, чем вторая труба?Решение:Составим для удобства таблицу:

 

V

v

t

1-я труба

360

v - 6

2-я труба

360

v

На 10 минут разница означает равенство:v2 - 6v - 216 = 0; v1 = -12 — не удовлетворяет условию, v2 = 18.В задаче спрашивается скорость работы первой трубы, т.е. 18 - 6 = 12 часов.Ответ: 12.Тренировочные задачиПример 7.Двое рабочих выполнили работу за два дня. Если бы первый рабочий проработал 2 дня, а второй 1 день, то они вместе выполнили бы всей работы. За сколько дней выполнит эту работу первый рабочий?Решение:

 

V
(объем работы)

v
(производительность)

t
(время работы)

Вместе

V = 1

х + у

1-й рабочий

2х

х

2

2-й рабочий

1у

у

1
Обозначим всю работу за 1, производительность первого рабочего за х, а производительность второго рабочего за у. Тогда, совместная производительность равна х + у. А на выполнение всей работы им потребуется 1/(х +у) дней, по условию: . За два дня первый рабочий сделает 2х, а второй рабочий — 1у, всего они выполнят 2х + у = 5/6. Получили систему: . Решая эту систему, найдем производительности рабочих: . Тогда время, которое затратит первый рабочий на выполнение всей работы равно: дня.Ответ: 3.Пример 8.Ученик прочел книгу в 480 страниц, ежедневно читая одинаковое количество страниц. Если бы он читал каждый день на 16 страниц больше, то прочел бы книгу на 5 дней раньше. Сколько дней ученик читал книгу?Решение:Пусть ученик читал в день x страниц. Тогда он прочитал книгу за дней. Если бы он читал x + 16 страниц в день, то он прочитал бы книгу за 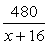дней, что на 5 дней меньше. Получаем уравнение: .Решая его, находим, что ученик в день читал x=32 страницы и прочитал книгу за 15 дней.Ответ: 15.Пример 9.Двое рабочих выполнили работу менее, чем за 4 часа. Если бы первый выполнял ее в одночку, он сделал бы работу на 6 часов быстрее, чем второй. Какие значения может принимать время выполнения работы первым из рабочих, работающим отдельно?Решение.Обозначим всю работу за 1, производительность первого рабочего за х, а производительность второго рабочего за у. Тогда, совместная производительность равна х + у. А на выполнение всей работы им потребуется дней, по условию: . Время, за которое может выполнить работу первый рабочий выражается: , а время второго: . По условию: .Итак, получили систему: .Так как производительность — величина положительная, то неравенства в системе равносильно следующему: 4x + 4y > 1. Выразим x из уравнения и подставим в неравенство: . Решая это неравенство, получаем: или . Условию соответствует первое неравенство. Следовательно, .Ответ: время выполнения работы первым из рабочих, работающим отдельно, может принимать значения, не большие 4.Список используемой литературы Видеолекция «Задачи на работу и производительность»:
Перейти к выполнению теста: Тест. Задачи на работу и производительность
В начало