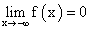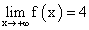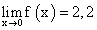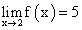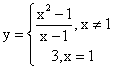Пределы функций
 — серьезный раздел высшей математики. «Анализируют» здесь довольно тонкие моменты: как ведет себя функция
— серьезный раздел высшей математики. «Анализируют» здесь довольно тонкие моменты: как ведет себя функция не только в целом, в своей области определения
не только в целом, в своей области определения (глобальный подход), но и около конкретной точки (локальный поход). Такой анализ практически всегда связан с понятием предела функции
(глобальный подход), но и около конкретной точки (локальный поход). Такой анализ практически всегда связан с понятием предела функции . Изучение в дальнейшем производной
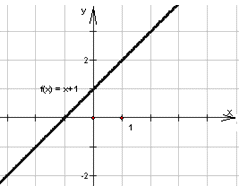
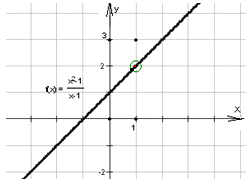
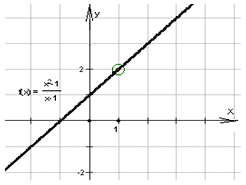
. Изучение в дальнейшем производной основано на понятии предела, поэтому так важно разбираться в данной теме.Определение и свойства пределов функцииФункция f (x) имеет предел A в точке x0, если для всех значений x, достаточно близких к x0 (в окрестности U(x0)), значение f (x) близко к A. При этом x0 может не принадлежать области определения функции D(f) , хотя окрестность точки x0 U (x0) принадлежит D(f). На графике это выглядит как выколотая точка.
основано на понятии предела, поэтому так важно разбираться в данной теме.Определение и свойства пределов функцииФункция f (x) имеет предел A в точке x0, если для всех значений x, достаточно близких к x0 (в окрестности U(x0)), значение f (x) близко к A. При этом x0 может не принадлежать области определения функции D(f) , хотя окрестность точки x0 U (x0) принадлежит D(f). На графике это выглядит как выколотая точка.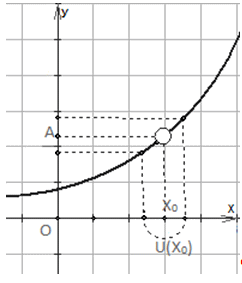 Обозначение:
Обозначение: 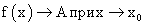 или:
или: 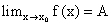 Рассмотрим с помощью некоторых известных графиков функций понятие предела на бесконечности.
Рассмотрим с помощью некоторых известных графиков функций понятие предела на бесконечности.
функция |
x → -∞ |
x → +∞ |
x → 0 |
f (x) = x2 |
→ +∞ |
→ +∞ |
→ 0 |
f (x) = 1 / x |
→ 0 |
→ 0 |
→ +∞, -∞ |
f (x) = x3 |
→ -∞ |
→ +∞ |
→ 0 |
 графика функции y = f (x), если выполняется одно из равенств:
графика функции y = f (x), если выполняется одно из равенств: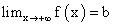 (рис. 1
(рис. 1  )или
)или 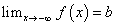 или
или 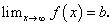 Прямая x = a является вертикальной асимптотой
Прямая x = a является вертикальной асимптотой графика функции y = f (x), если выполняется одно из равенств:
графика функции y = f (x), если выполняется одно из равенств: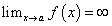 (рис. 2
(рис. 2  )или
)или 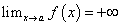 или
или 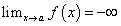 Прямая y = ax + b является наклонной асимптотой
Прямая y = ax + b является наклонной асимптотой графика функции y = f (x), если выполняется одно из равенств:
графика функции y = f (x), если выполняется одно из равенств: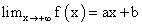 (рис. 3
(рис. 3  )или
)или 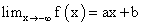 или
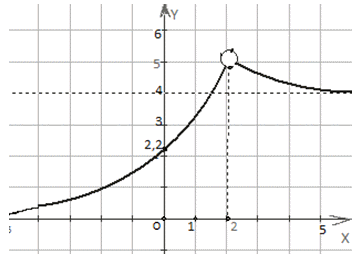
или  Пример.По графику y = f (x) найти:
Пример.По графику y = f (x) найти:
 Свойства пределов функции
Свойства пределов функции- Предел постоянной величины равен самой постоянной величине:
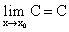
- Предел суммы двух функций равен сумме пределов этих функций:
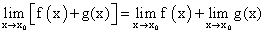 Аналогично предел разности двух функций равен разности пределов этих функций.
Аналогично предел разности двух функций равен разности пределов этих функций. - Постоянный коэффициент можно выносить за знак предела:
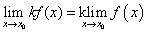
- Предел произведения двух функций равен произведению пределов этих функций:
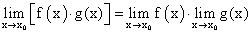
- Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
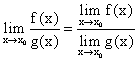
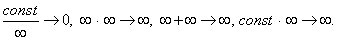 Следующие пределы считают неопределенностью
Следующие пределы считают неопределенностью :
: 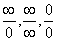 . Если в примере встретилась неопределенность, то надо найти пути для ее устранения. Общие правила:
. Если в примере встретилась неопределенность, то надо найти пути для ее устранения. Общие правила:- 1) если в числителе и знаменателе находятся многочлены
 , и имеется неопределенности вида
, и имеется неопределенности вида 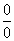 или
или 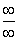 , то для решения нужно разложить числитель и знаменатель на множители или разделить на максимальную степень числителя (или знаменателя) и числитель и знаменатель;2) если же в числителе или в знаменателе находятся иррациональные выражения
, то для решения нужно разложить числитель и знаменатель на множители или разделить на максимальную степень числителя (или знаменателя) и числитель и знаменатель;2) если же в числителе или в знаменателе находятся иррациональные выражения и имеется неопределенности вида
и имеется неопределенности вида 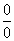 или
или 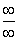 , то для решения надо избавляться от иррациональности, помножив и числитель, и знаменатель на сопряженное выражение;3) если же в числителе или в знаменателе находятся тригонометрические выражения
, то для решения надо избавляться от иррациональности, помножив и числитель, и знаменатель на сопряженное выражение;3) если же в числителе или в знаменателе находятся тригонометрические выражения и имеется неопределенности вида
и имеется неопределенности вида 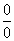 или
или 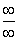 , то для решения используют формулу замечательного предела
, то для решения используют формулу замечательного предела 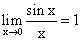
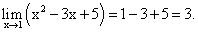 Пример 2.Найти предел функции:
Пример 2.Найти предел функции: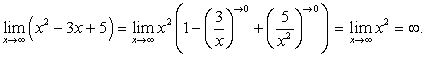 Пример 3.Найти предел функции:
Пример 3.Найти предел функции: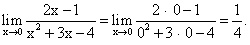 Пример 4.Найти предел функции:
Пример 4.Найти предел функции: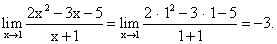 Пример 5.Найти предел функции:
Пример 5.Найти предел функции: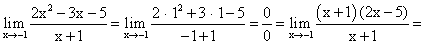
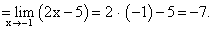 Пример 6.Найти предел функции:
Пример 6.Найти предел функции: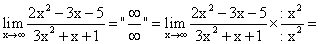
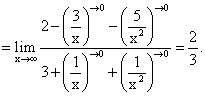 Пример 7.Найти предел функции:
Пример 7.Найти предел функции: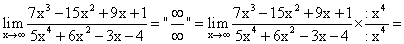
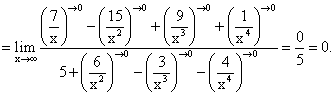 Пример 8.Найти предел функции:
Пример 8.Найти предел функции: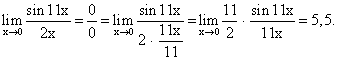 Пример 9.Найти предел функции:
Пример 9.Найти предел функции: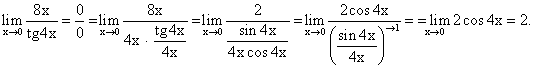 Пример 10.Найти предел функции:
Пример 10.Найти предел функции: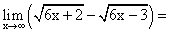
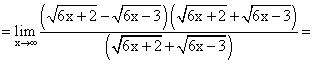
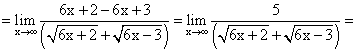
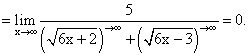 Непрерывность функцииМы интуитивно понимаем, что если функция непрерывна, то мы можем ее нарисовать, не отрывая карандаша от листа бумаги.Функция у = f (x) называется непрерывной
Непрерывность функцииМы интуитивно понимаем, что если функция непрерывна, то мы можем ее нарисовать, не отрывая карандаша от листа бумаги.Функция у = f (x) называется непрерывной , если она непрерывна в каждой точке своей области определения.Чтобы понять, что такое непрерывность функции
, если она непрерывна в каждой точке своей области определения.Чтобы понять, что такое непрерывность функции в целом, сначала надо разобраться, что такое непрерывность функции в точке
в целом, сначала надо разобраться, что такое непрерывность функции в точке .Функция у = f (x) называется непрерывной в точке х = с, если предел функции в точке х = с равен значению функции в этой точке:
.Функция у = f (x) называется непрерывной в точке х = с, если предел функции в точке х = с равен значению функции в этой точке: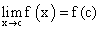 Т.е. должны выполняться одновременно три условия:
Т.е. должны выполняться одновременно три условия:- 1) функция определена и в самой точке х = с и в некоторой окрестности этой точки, причем U(с) ϵ D(f);2) существует
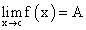 ;3) A = f(c).
;3) A = f(c).Непрерывная функция |
Разрывная в т. х = 1 |
Разрывная в т. х = 1 |
|
|
|
|
|
|
|
|
|
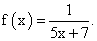 РешениеНайдем область определения функции: 5x + 7 ≠ 0, x ≠ -1,4.Ответ: -1,4.Пример 12.Найти сумму значений точек разрыва функции
РешениеНайдем область определения функции: 5x + 7 ≠ 0, x ≠ -1,4.Ответ: -1,4.Пример 12.Найти сумму значений точек разрыва функции 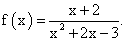 РешениеНайдем область определения функции: х2 + 2х — 3 ≠ 0. По теореме, обратной к теореме Виета: х1 ≠ 1, x2 ≠ -3.Далее находим сумму значений 1 + (-3) = -2.Ответ: -2.Пример 13.Указать точку разрыва функции:
РешениеНайдем область определения функции: х2 + 2х — 3 ≠ 0. По теореме, обратной к теореме Виета: х1 ≠ 1, x2 ≠ -3.Далее находим сумму значений 1 + (-3) = -2.Ответ: -2.Пример 13.Указать точку разрыва функции: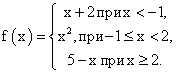
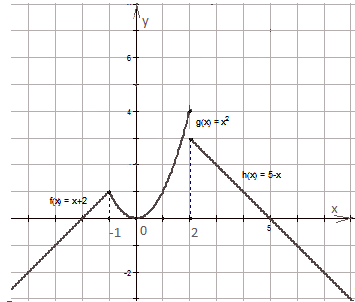 РешениеПостроим график данной функции на указанных промежутках. Видим, что целостность функции нарушается при х = 2.Ответ: 2.Список используемой литературы Видеолекция «Пределы функций»:
РешениеПостроим график данной функции на указанных промежутках. Видим, что целостность функции нарушается при х = 2.Ответ: 2.Список используемой литературы Видеолекция «Пределы функций»: