Функции. Графики элементарных функций
 . При этом, безусловно, требуется следующие базовые знания.
. При этом, безусловно, требуется следующие базовые знания.- О графиках основных элементарных функций
 :
:
- Об элементарных приемах построения графиков
 :
:- а) приемы, связанные с применением геометрических преобразований плоскости (параллельный перенос, симметрия, деформация);б) приемы построения графиков кусочных функций
 , т.е. функций, заданных различными формулами на разных участках области определения, например, функция:
, т.е. функций, заданных различными формулами на разных участках области определения, например, функция: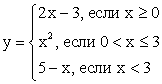 в) приемы так называемого «сложения» графиков функций
в) приемы так называемого «сложения» графиков функций .
.
 , если каждому значению x соответствует определенное значение y.Множество всех тех значений, которые принимает аргумент x функции y = f (x), называется областью определения
, если каждому значению x соответствует определенное значение y.Множество всех тех значений, которые принимает аргумент x функции y = f (x), называется областью определения этой функции.Множество всех тех значений, которые принимает сама функция y = f (x), называется областью значений (изменения)
этой функции.Множество всех тех значений, которые принимает сама функция y = f (x), называется областью значений (изменения) этой функции.Функция y = f (x) называется четной
этой функции.Функция y = f (x) называется четной , если при всех значений x из области определения этой функции f (-x) = f (x).Функция y = f (x) называется нечетной
, если при всех значений x из области определения этой функции f (-x) = f (x).Функция y = f (x) называется нечетной , если при всех значений x из области определения этой функции f (-x) = -f (x).Область определения четной и нечетной функции симметрична относительно начала координат.Функция y = f (x) называется возрастающей (убывающей)
, если при всех значений x из области определения этой функции f (-x) = -f (x).Область определения четной и нечетной функции симметрична относительно начала координат.Функция y = f (x) называется возрастающей (убывающей) на данном промежутке, если при произвольных двух различных значениях аргумента из данного промежутка большему значению аргумента соответствует большее (меньшее) значение функции.Функция y = f (x) называется периодической
на данном промежутке, если при произвольных двух различных значениях аргумента из данного промежутка большему значению аргумента соответствует большее (меньшее) значение функции.Функция y = f (x) называется периодической , с периодом T, где T ≠ 0, если значение функции не изменяется при прибавлении числа T к любому допустимому значению аргумента: f (x+T) = f (x).Функция y = f (x) называется ограниченной
, с периодом T, где T ≠ 0, если значение функции не изменяется при прибавлении числа T к любому допустимому значению аргумента: f (x+T) = f (x).Функция y = f (x) называется ограниченной , если можно указать такое положительное число M, что |f (x)| ≤ M для всех значений x из области определения функции. Если же точка M не существует, то функция называется неограниченной
, если можно указать такое положительное число M, что |f (x)| ≤ M для всех значений x из области определения функции. Если же точка M не существует, то функция называется неограниченной .Графиком функции y = f (x)
.Графиком функции y = f (x) называется множество всех точек плоскости, координаты которых (x, f (x)).Функцию вида y = ax2 + bx + c называют квадратичной
называется множество всех точек плоскости, координаты которых (x, f (x)).Функцию вида y = ax2 + bx + c называют квадратичной . Графиком квадратичной функции является кривая, называемая параболой
. Графиком квадратичной функции является кривая, называемая параболой . Точку с координатами
. Точку с координатами 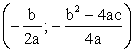 называют вершиной параболы
называют вершиной параболы .Соответствие между элементами двух множеств X и Y, при котором каждому элементу множества X сопоставляется не более одного элемента Y, называется функцией
.Соответствие между элементами двух множеств X и Y, при котором каждому элементу множества X сопоставляется не более одного элемента Y, называется функцией .Отсюда следует, что понятие функции имеет три главных компонента:
.Отсюда следует, что понятие функции имеет три главных компонента:- 1) множество X (которое называется областью определения функции);2) множество Y (которое называется областью значений функции);3) закон соответствия
 (который иногда называется функциональной зависимостью
(который иногда называется функциональной зависимостью ).
).Аналитическая формула |
Ограничения |
|
|
|
|
|
|
|
|
|
|
|
|
- Способ «по точкам». Вытекает из определения графика функции. Он является длинным и недостаточно надежным. Применяется в школьном курсе математики при первоначальном знакомстве с простейшими функциями.
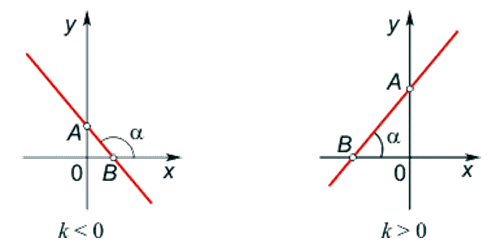
- Способ «путем сдвига графиков основных функций или сдвига осей координат». Чтобы построить график функции y = f (x) + c можно или график функции y = f (x) сдвинуть вдоль оси 0y на c единиц в сторону, совпадающую со знаком c, или перенести параллельно ось 0y в сторону, противоположную знаку c.Чтобы построить график функции y = f (x + b), можно или график функции y = f (x) вдоль оси 0x на b единиц в сторону, противоположную знаку b, или перенести параллельно ось 0y в сторону, совпадающую со знаком b.
- Способ «путем симметричного отображения относительно осей координат». Чтобы построить график функции y = -f (x), можно построить изображение, симметричное графику функции y = f (x) относительно оси абсцисс.Чтобы построить график функции y = f (-x), можно построить изображение, симметричное графику функции y = f (x) относительно оси ординат.
- Способ «путем деформирования графиков основных функций». Чтобы построить график функции y = af (x) при a > 0, можно график исходной функции растянуть (сжать) вдоль оси ординат, если a > 1 (0 < a < 1).Чтобы построить график функции y = f (b ∙ x) при b > 0, можно график исходной функции растянуть (сжать) вдоль оси абсцисс, если b > 1 (0 < b < 1).
- «Способы построения графиков функций, аналитическое выражение которых содержит знак абсолютной величины»:
- 1) функция y = f (|x|) четная. Чтобы построить ее график, достаточно построить для всех неотрицательных значении аргумента график функции y = f (x), а затем достроить его левую часть, симметричную правой относительно оси ординат;2) рассмотрим далее, как строить функцию y = |f (x)|. Можно данную функцию рассматривать как совокупность двух функций:
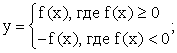 3) чтобы построить график функции y = |f (x)|, достаточно построить график функции y = f (x) и ту часть графика, которая расположена в нижней полуплоскости, симметрично отразить относительно оси абсцисс;4) вспомним, как строится функция y = f (|x|).Функция y = f (|x|) четная. Построить для всех неотрицательных значений аргумента график функции y = f (x), затем его симметрично отразить относительно оси ординат, и, наконец, ту часть полученного графика, которая расположена в нижней полуплоскости, симметрично отразить относительно оси абсцисс.
3) чтобы построить график функции y = |f (x)|, достаточно построить график функции y = f (x) и ту часть графика, которая расположена в нижней полуплоскости, симметрично отразить относительно оси абсцисс;4) вспомним, как строится функция y = f (|x|).Функция y = f (|x|) четная. Построить для всех неотрицательных значений аргумента график функции y = f (x), затем его симметрично отразить относительно оси ординат, и, наконец, ту часть полученного графика, которая расположена в нижней полуплоскости, симметрично отразить относительно оси абсцисс. - Способ «кусочно-линейная функция».Графиком кусочно-линейной функции
 является ломаная линия. Для построения графика находят уравнения звеньев ломаной.
является ломаная линия. Для построения графика находят уравнения звеньев ломаной.
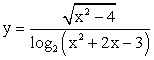 РешениеЧтобы найти область определения данной функции, следует решить систему неравенств:
РешениеЧтобы найти область определения данной функции, следует решить систему неравенств: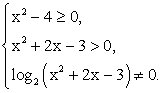 Ответ:
Ответ: 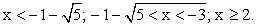 Комментарий. Область значений (изменения) функции можно найти, исследуя аналитическое выражение функции или разрешая данное уравнение функции относительно x.Пример 2.Найти область изменения функции
Комментарий. Область значений (изменения) функции можно найти, исследуя аналитическое выражение функции или разрешая данное уравнение функции относительно x.Пример 2.Найти область изменения функции 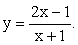 РешениеПервый способ. Область определения данной функции x ≠ -1. Для нахождения области изменения удобно данную функцию записать в таком виде:
РешениеПервый способ. Область определения данной функции x ≠ -1. Для нахождения области изменения удобно данную функцию записать в таком виде: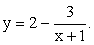 Дробь
Дробь 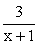 принимает в области определения функции всевозможные значения, кроме нуля. Следовательно, областью изменения данной функции является множество всех действительных чисел, кроме y = 2.Второй способ. Разрешают данное уравнение функции относительно x. Получают
принимает в области определения функции всевозможные значения, кроме нуля. Следовательно, областью изменения данной функции является множество всех действительных чисел, кроме y = 2.Второй способ. Разрешают данное уравнение функции относительно x. Получают 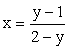 . Откуда следует, что y может быть любым действительным числом, кроме 2.Ответ:
. Откуда следует, что y может быть любым действительным числом, кроме 2.Ответ: 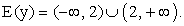 Пример 3.Найти область изменения функции
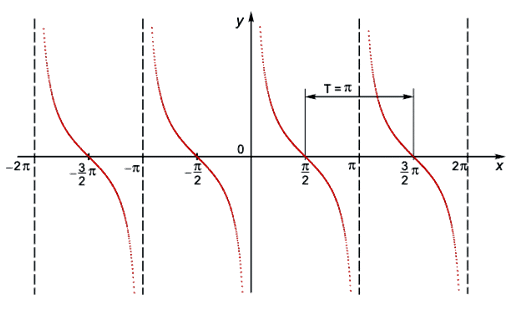
Пример 3.Найти область изменения функции 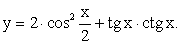 РешениеОбласть определения данной функции
РешениеОбласть определения данной функции 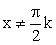 , где k ϵ Z. На этой области данная функция и функция
, где k ϵ Z. На этой области данная функция и функция 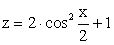 имеют одну и ту же область изменения. Найдем область изменения функции z:
имеют одну и ту же область изменения. Найдем область изменения функции z: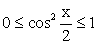 , откуда следует, что
, откуда следует, что 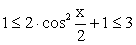 .Далее следует исключить из области изменения z те значения, которые z принимает при:
.Далее следует исключить из области изменения z те значения, которые z принимает при: 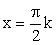
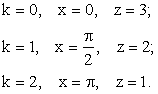 При других значениях k значения z совпадают с одним из полученных трех значений, которые эта функция принимает только при
При других значениях k значения z совпадают с одним из полученных трех значений, которые эта функция принимает только при 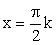 .Следовательно, областью изменения функции
.Следовательно, областью изменения функции 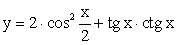 являются действительные числа, удовлетворяющие неравенствам:1 < y < 2; 2 < y < 3.Ответ:
являются действительные числа, удовлетворяющие неравенствам:1 < y < 2; 2 < y < 3.Ответ: 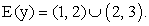 .Пример 4.Построить график функции
.Пример 4.Построить график функции 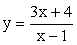 (без использования понятия производной).РешениеДана функция
(без использования понятия производной).РешениеДана функция 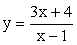 . Преобразуем
. Преобразуем 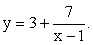
- Область определения:
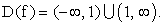
- Область значений:
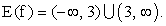
- Четность, нечетность: и ни четная, ни нечетная
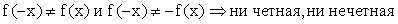 .
. - Монотонность: убывает во всей области определения
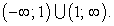
- Пересечение с осями 0x и 0y:
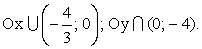
- Промежутки знакопостоянства:
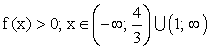
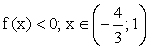
- Поведение функции вблизи точек разрыва и при
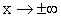 :
: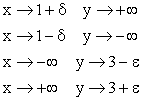
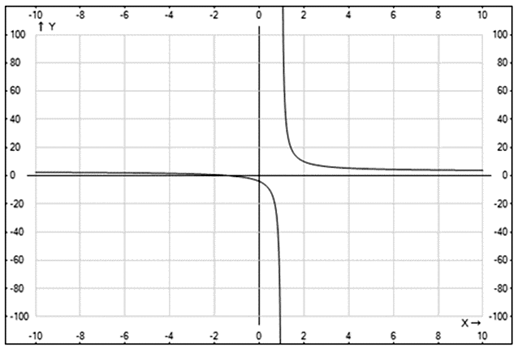 Комментарий. При построении графика функции следует найти точки, в которых он пересекает оси координат, а также выяснить поведение функции при x, стремящемся к ± ∞ в случае, когда ее область определения не ограничена. Необходимо также исследовать поведение функции вблизи тех точек, в которых она не определена.Пример 5.Построить графики следующих функций:
Комментарий. При построении графика функции следует найти точки, в которых он пересекает оси координат, а также выяснить поведение функции при x, стремящемся к ± ∞ в случае, когда ее область определения не ограничена. Необходимо также исследовать поведение функции вблизи тех точек, в которых она не определена.Пример 5.Построить графики следующих функций:  Решение
Решение- Рассмотрим функцию y = |x|. Она определена на всей оси 0x, четная. Ее график состоит из двух лучей, выходящих из начала координат и направленных по биссектрисам I и II координатных углов:
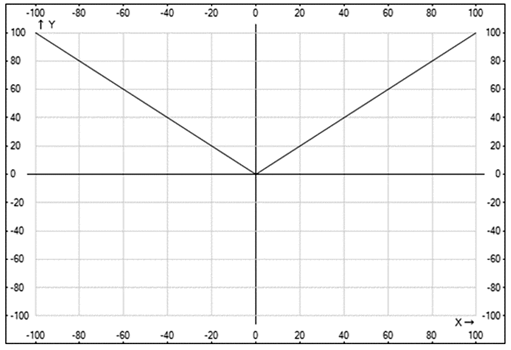
- Обратимся к функции y = 2|x|. Она определена на всей оси 0x, четная. На рисунке приведен ее график, причем он построен из двух половинок y = 2x, при x ≥ 0 и y = 2x, при x < 0:
- Функция
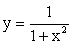 определена на всей оси 0x, она четная:
определена на всей оси 0x, она четная: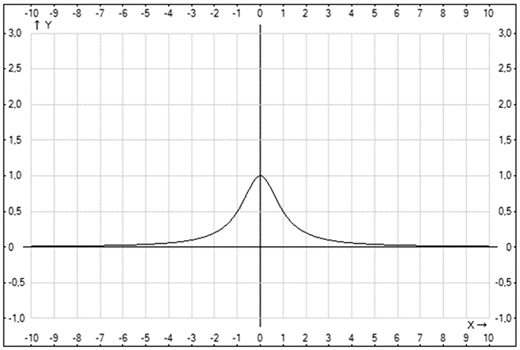 Поскольку знаменатель дроби 1 + x2 ≥ 1 при любом x, то 0 < y ≤ 1. В точке x = 0 функция достигает своего наибольшего значения. При неограниченном возрастании x величина y становится сколь угодно близкой к нулю (стремится к нулю).
Поскольку знаменатель дроби 1 + x2 ≥ 1 при любом x, то 0 < y ≤ 1. В точке x = 0 функция достигает своего наибольшего значения. При неограниченном возрастании x величина y становится сколь угодно близкой к нулю (стремится к нулю). - Рассмотрим функцию
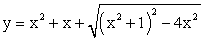 .По определению арифметического корня имеем:
.По определению арифметического корня имеем: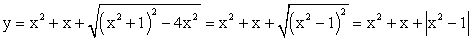 Однако:
Однако: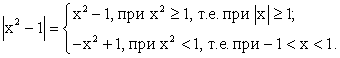 Следовательно:
Следовательно: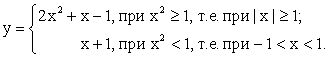
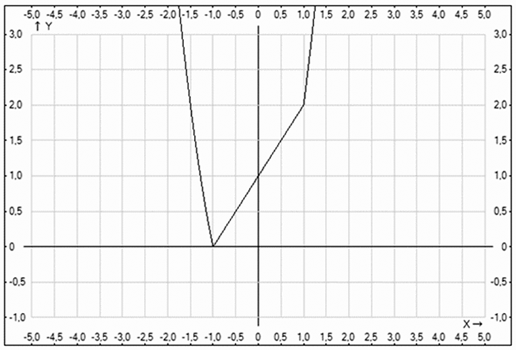 Пример 6.Построить график функции
Пример 6.Построить график функции 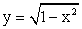 на основании результатов исследования функции.РешениеДля построения графика функции исследуем ее, придерживаясь общей схемы исследования.
на основании результатов исследования функции.РешениеДля построения графика функции исследуем ее, придерживаясь общей схемы исследования.- Нахождение области определения:
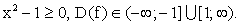
- Определение четности или нечетности:
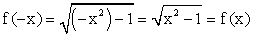 Функция
Функция 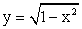 — четная.Дальнейшее исследование будем проводить для
— четная.Дальнейшее исследование будем проводить для 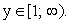 .
. - Область изменения функции.Если x = 1, то y = 0. Если x → ∞, то y → ∞. Следовательно,
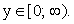 .
. - Пересечение с координатными осями.Если
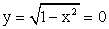 , то x = ±1. Пересечений с осью 0y нет, т.к. x = 0 не входит в область определения функции.
, то x = ±1. Пересечений с осью 0y нет, т.к. x = 0 не входит в область определения функции. - Выделение промежутков монотонности.Для x1 > x2 ≥ 1 рассмотрим разность:
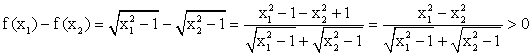 При возрастании значений x от 1 до ∞ значения y возрастают.
При возрастании значений x от 1 до ∞ значения y возрастают. - Нахождение корней функции и промежутков знакопостоянства.Если x ϵ [1; ∞), то
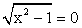 при x = 1,
при x = 1, 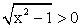 при всех x ϵ [1; ∞).
при всех x ϵ [1; ∞).
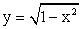
 Пример 7.Постройте график функции y = x3 — 6x2 + 12x — 9 и опишите ее свойства.РешениеПреобразуем аналитическое выражение данной функции, выделив полный куб разности:x3 — 6x2 + 12x — 9 = (x3 — 6x2 + 12x — 8) — 1 = (x — 2)3 — 1.Таким образом, необходимо построить график функции y = (x — 2)3 — 1.Это легко сделать, осуществив параллельный перенос базового графика функции y = x3, на 2 единичных отрезка вдоль оси 0х вправо и на 1 единичный отрезок вдоль оси 0у вниз. Искомый график изображен на рисунке:
Пример 7.Постройте график функции y = x3 — 6x2 + 12x — 9 и опишите ее свойства.РешениеПреобразуем аналитическое выражение данной функции, выделив полный куб разности:x3 — 6x2 + 12x — 9 = (x3 — 6x2 + 12x — 8) — 1 = (x — 2)3 — 1.Таким образом, необходимо построить график функции y = (x — 2)3 — 1.Это легко сделать, осуществив параллельный перенос базового графика функции y = x3, на 2 единичных отрезка вдоль оси 0х вправо и на 1 единичный отрезок вдоль оси 0у вниз. Искомый график изображен на рисунке: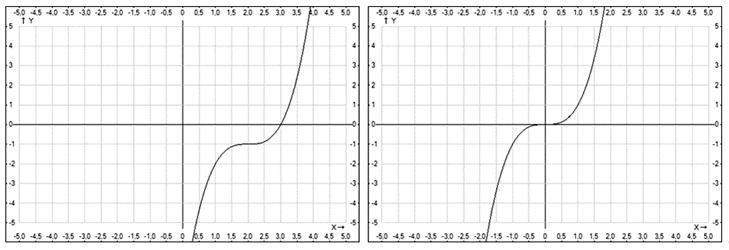 При построении мы уточнили точки пересечения графика с осями системы координат; рядом построен график базовой функции y = x3.При построении данного графика можно было поступить иначе: ввести вспомогательную систему координат x’0’y’ с началом в точке 0’ (2, -1) и построить в этой новой системе координат график функции y = x3. Ясно, что в исходной (основной) системе — это искомый график: y = (x —2)3 — 1. В дальнейшем, применяя параллельный перенос для построения графиков, мы будем пользоваться именно этим приемом. Он позволяет параллельный перенос кривой — графика базовой функции заменить параллельным переносом прямых — осей координат, что намного удобней.Пример 8.Построить график функции
При построении мы уточнили точки пересечения графика с осями системы координат; рядом построен график базовой функции y = x3.При построении данного графика можно было поступить иначе: ввести вспомогательную систему координат x’0’y’ с началом в точке 0’ (2, -1) и построить в этой новой системе координат график функции y = x3. Ясно, что в исходной (основной) системе — это искомый график: y = (x —2)3 — 1. В дальнейшем, применяя параллельный перенос для построения графиков, мы будем пользоваться именно этим приемом. Он позволяет параллельный перенос кривой — графика базовой функции заменить параллельным переносом прямых — осей координат, что намного удобней.Пример 8.Построить график функции 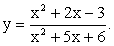 РешениеРешим квадратные уравнения x2 + 2x — 3 = 0 и x2 + 5x + 6 = 0 и преобразуем дробь из аналитического выражения функции:
РешениеРешим квадратные уравнения x2 + 2x — 3 = 0 и x2 + 5x + 6 = 0 и преобразуем дробь из аналитического выражения функции: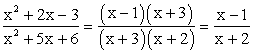 Таким образом, исходная функция
Таким образом, исходная функция 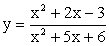 тождественна функции
тождественна функции 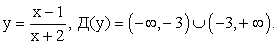 Функция
Функция 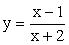 — дробно-линейная, ее графиком является гипербола. Значит, график функции
— дробно-линейная, ее графиком является гипербола. Значит, график функции 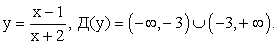 , т.е. график «исходной» функции
, т.е. график «исходной» функции 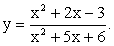 — гипербола, «выколотая» в точке x = -3.Построим график дробно-линейной функции
— гипербола, «выколотая» в точке x = -3.Построим график дробно-линейной функции 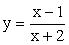 . Для этого преобразуем дробь
. Для этого преобразуем дробь 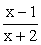 к виду
к виду 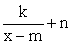 :
: 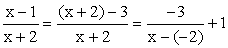 . Для построения графика функции
. Для построения графика функции 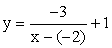 введем вспомогательную систему координат x’0’y’ с началом в точке 0’ (2, -1). В этой новой системе координат построим график соответствующей базовой функции
введем вспомогательную систему координат x’0’y’ с началом в точке 0’ (2, -1). В этой новой системе координат построим график соответствующей базовой функции 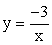 (уточнив при этом точки пересечения с осями основной системы координат х0у). И, наконец, «выколем» точку x = -3. В основной системе координат полученная «выколотая» гипербола, и будет графиком данной функции
(уточнив при этом точки пересечения с осями основной системы координат х0у). И, наконец, «выколем» точку x = -3. В основной системе координат полученная «выколотая» гипербола, и будет графиком данной функции 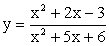 :
: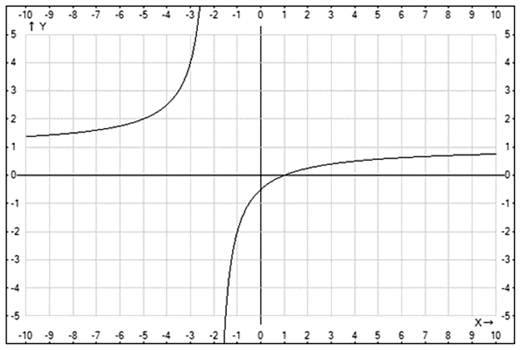 Пример 9.Построить график функции y = |x2 — 2|x|-8| и описать ее свойства.РешениеДля построения искомого графика, учитывая тождество |x|2 = x2, воспользуемся известным правилом построения графика функции y = |f (|x|)| исходя из графика базовой функции y = f (x), т.е. симметрией относительно осей системы координат. Базовой функцией в данном случае является функция y = x2 — 2x — 8.Искомый график изображен на рисунке:
Пример 9.Построить график функции y = |x2 — 2|x|-8| и описать ее свойства.РешениеДля построения искомого графика, учитывая тождество |x|2 = x2, воспользуемся известным правилом построения графика функции y = |f (|x|)| исходя из графика базовой функции y = f (x), т.е. симметрией относительно осей системы координат. Базовой функцией в данном случае является функция y = x2 — 2x — 8.Искомый график изображен на рисунке: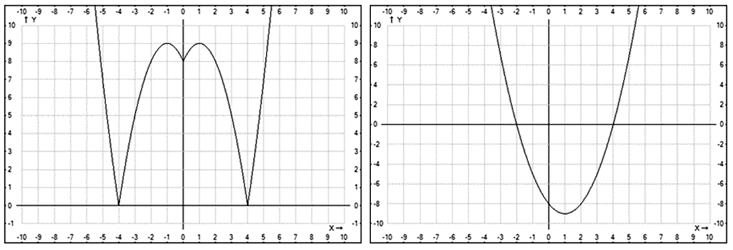 Пример 10.Построить график функции y = |x2 —4x + 3| + |x —4|.РешениеРаскроем модули, входящие в аналитическое выражение функции и перейдем тем самым к кусочному заданию данной функции:
Пример 10.Построить график функции y = |x2 —4x + 3| + |x —4|.РешениеРаскроем модули, входящие в аналитическое выражение функции и перейдем тем самым к кусочному заданию данной функции: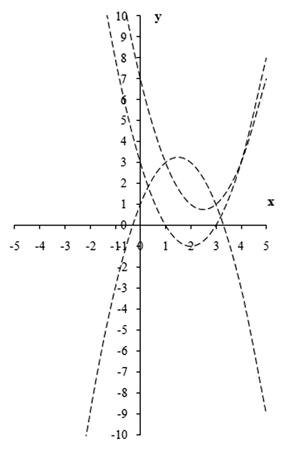
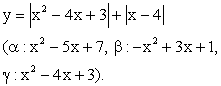
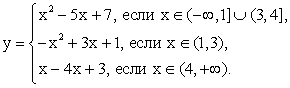 Следовательно, задача свелась к построению графика кусочно-квадратичной функции:
Следовательно, задача свелась к построению графика кусочно-квадратичной функции: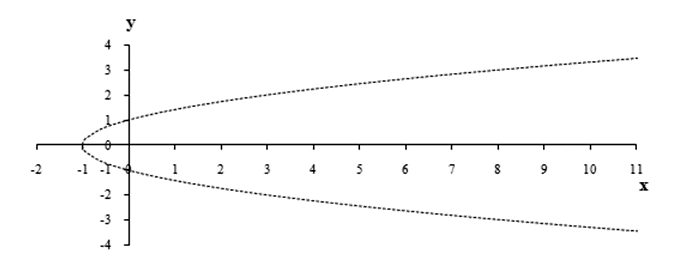 Построения проводились следующим образом: были построены «пунктиром» параболы и y = x2 — 5x + 7, y = -x2 + 3x + 1 и y = x2 — 4x + 3, а затем «сплошной линией» выделены необходимые «куски» парабол в соответствии с условиями на х из «кусочного аналитического выражения» функции. Параболы строились обычным образом: «по точкам» (вершине, точкам пересечения с осями координат и уточняющим точкам, особым для кусочной функции); x = 1, x = 3, x = 4.Пример 11.Построим график функции
Построения проводились следующим образом: были построены «пунктиром» параболы и y = x2 — 5x + 7, y = -x2 + 3x + 1 и y = x2 — 4x + 3, а затем «сплошной линией» выделены необходимые «куски» парабол в соответствии с условиями на х из «кусочного аналитического выражения» функции. Параболы строились обычным образом: «по точкам» (вершине, точкам пересечения с осями координат и уточняющим точкам, особым для кусочной функции); x = 1, x = 3, x = 4.Пример 11.Построим график функции 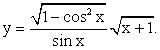 .РешениеПреобразуем аналитическое выражение функции:
.РешениеПреобразуем аналитическое выражение функции: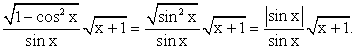 Таким образом, можно перейти к кусочному заданию данной функции:
Таким образом, можно перейти к кусочному заданию данной функции: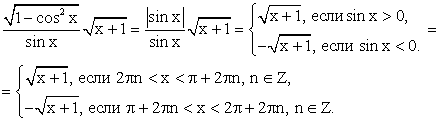 График этой кусочной функции, состоящий из «кусков» графиков функций
График этой кусочной функции, состоящий из «кусков» графиков функций 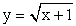 и
и 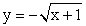 , изображен на рисунке:
, изображен на рисунке: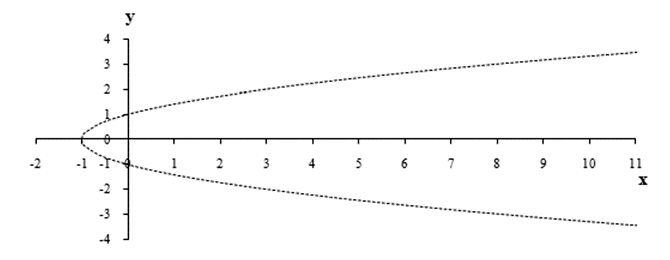 При его построении учитывалась естественно, область определения функции:
При его построении учитывалась естественно, область определения функции: 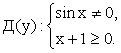 Пример 12.Построим график функции
Пример 12.Построим график функции 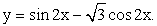 .РешениеПреобразуем аналитическое выражение функции:
.РешениеПреобразуем аналитическое выражение функции: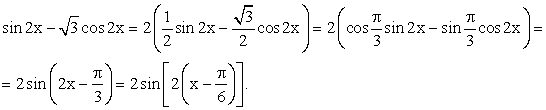 Итак, необходимо построить график функции
Итак, необходимо построить график функции 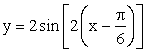 .
.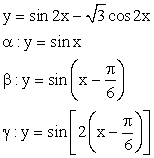 Строим сначала синусоиду y = sin x. Это базовый график. Затем, осуществив параллельный перенос вдоль оси 0х вправо на
Строим сначала синусоиду y = sin x. Это базовый график. Затем, осуществив параллельный перенос вдоль оси 0х вправо на 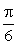 , получаем график функции
, получаем график функции 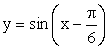 . Далее, строим график функции
. Далее, строим график функции 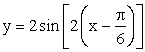 , который получается из предыдущего равномерным сжатием в 2 раза вдоль оси 0х. И, наконец, растяжением последнего графика в 2 раза вдоль оси 0у получаем график исходной функции. График изображен на рисунке (пунктиром показаны промежуточные построения):
, который получается из предыдущего равномерным сжатием в 2 раза вдоль оси 0х. И, наконец, растяжением последнего графика в 2 раза вдоль оси 0у получаем график исходной функции. График изображен на рисунке (пунктиром показаны промежуточные построения):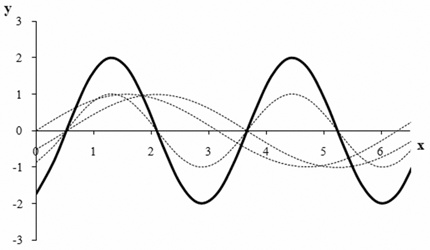 При этом, поскольку базовая функция y = sin x — периодическая с основным периодом 2π, то все построения мы проводили на отрезке оси 0х длиной 2π: [2π]. Полученный график нетрудно продолжить на всей области определения.Пример 13.Построить график функции
При этом, поскольку базовая функция y = sin x — периодическая с основным периодом 2π, то все построения мы проводили на отрезке оси 0х длиной 2π: [2π]. Полученный график нетрудно продолжить на всей области определения.Пример 13.Построить график функции 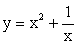 .РешениеЧасто задача построения графика функции y = f (x) = f1 (x) + f2 (x) значительно облегчается, если предварительно построить в одной системе координат графики функций y = f1 (x) и y = f2 (x).В нашем случае
.РешениеЧасто задача построения графика функции y = f (x) = f1 (x) + f2 (x) значительно облегчается, если предварительно построить в одной системе координат графики функций y = f1 (x) и y = f2 (x).В нашем случае 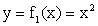 и
и 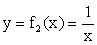 .Целесообразен следующий план построения графика данной функции.
.Целесообразен следующий план построения графика данной функции.- Построим график функции y = x2.
- Построим график функции
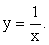 .
. - Проанализируем, каким будет значение функции
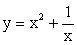 (назовем ее «суммарной») в характерных точках: x1 = 0; x2 = 1; вообще в контексте рассматриваемого приема построения графиков, к характерным точкам целесообразно относить нули функций y = f1 (x) и y = f2 (x), их точки разрыва, граничные точки, точки экстремума и точки излома, точки пересечения графиков функций y = f1 (x) и y = f2 (x).
(назовем ее «суммарной») в характерных точках: x1 = 0; x2 = 1; вообще в контексте рассматриваемого приема построения графиков, к характерным точкам целесообразно относить нули функций y = f1 (x) и y = f2 (x), их точки разрыва, граничные точки, точки экстремума и точки излома, точки пересечения графиков функций y = f1 (x) и y = f2 (x). - Исходя из графиков функций y = f1 (x) и y = f2 (x) проанализируем поведение графика суммарной функции на бесконечности.
- Уточним график «суммарной» функции, осуществив непосредственное сложение ординат y1 и y2 в нескольких дополнительных точках.
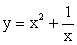 .В особой точке x1 = 0 данная функция неопределенна, поскольку, неопределенна функция
.В особой точке x1 = 0 данная функция неопределенна, поскольку, неопределенна функция 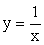 . Прямая х = 0 (ось 0у) будет вертикальной асимптотой графика функции
. Прямая х = 0 (ось 0у) будет вертикальной асимптотой графика функции 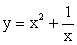 (так же, как и графика функции
(так же, как и графика функции 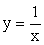 ):В особой точке x2 = 1 имеем: y = y1 + y2 = 1 + 1 = 2.Проанализируем поведение графика суммарной функции на бесконечности:Наконец, рассмотрим несколько дополнительных уточняющих точек. Особенно важно понять взаимное расположение графиков функций y = f1 (x) и y = f2 (x) и суммарной функции вблизи асимптоты х = 0 и на бесконечности. Пусть x = -1, тогда y1 = 1, y2 = -1 и y = y1 + y2 = 0. Это точка пересечения искомого графика с осью 0х. Пусть
):В особой точке x2 = 1 имеем: y = y1 + y2 = 1 + 1 = 2.Проанализируем поведение графика суммарной функции на бесконечности:Наконец, рассмотрим несколько дополнительных уточняющих точек. Особенно важно понять взаимное расположение графиков функций y = f1 (x) и y = f2 (x) и суммарной функции вблизи асимптоты х = 0 и на бесконечности. Пусть x = -1, тогда y1 = 1, y2 = -1 и y = y1 + y2 = 0. Это точка пересечения искомого графика с осью 0х. Пусть 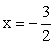 , тогда
, тогда 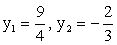 и
и 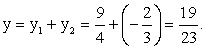 Пусть x = -2, тогда
Пусть x = -2, тогда 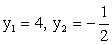 и
и 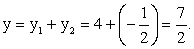 Пусть x = -3, тогда
Пусть x = -3, тогда 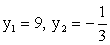 и
и 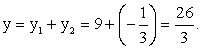 Проанализируем разность y1 — y (обозначим ее ∆y) для взятых значений x:Возьмем x = -10. Тогда
Проанализируем разность y1 — y (обозначим ее ∆y) для взятых значений x:Возьмем x = -10. Тогда 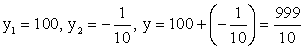 , т.е.
, т.е. 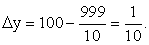 Ясно, что по мере увеличения |x|, ∆y уменьшается, оставаясь положительной; кроме того, ясно, что ∆y = |y2|. При стремлении к -∞ значения функции
Ясно, что по мере увеличения |x|, ∆y уменьшается, оставаясь положительной; кроме того, ясно, что ∆y = |y2|. При стремлении к -∞ значения функции 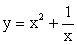 все меньше отличаются от значений функции y = x2 и отличие это определяется значениями функции
все меньше отличаются от значений функции y = x2 и отличие это определяется значениями функции 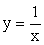 , стремящейся к нулю, но всегда отрицательными. Таким образом, график функции
, стремящейся к нулю, но всегда отрицательными. Таким образом, график функции 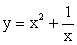 , при стремлении к -∞, все более приближается к графику функции y = x2, но оставаясь всегда ниже его.Приведенные выше рассуждения при построении графика функции
, при стремлении к -∞, все более приближается к графику функции y = x2, но оставаясь всегда ниже его.Приведенные выше рассуждения при построении графика функции 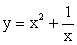 придется повторить с соответствующими поправками еще трижды (именно с этим и связана та детальная подробность, с которой эти рассуждения представлены выше). Предоставим возможность нашим читателем порассуждать самостоятельно и приведем далее лишь выводы, результаты этих рассуждений:
придется повторить с соответствующими поправками еще трижды (именно с этим и связана та детальная подробность, с которой эти рассуждения представлены выше). Предоставим возможность нашим читателем порассуждать самостоятельно и приведем далее лишь выводы, результаты этих рассуждений:- при стремлении к нулю слева график функции
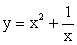 все более приближается к графику функции
все более приближается к графику функции 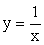 , но оставаясь всегда выше его (график суммарной функции оказывается как бы «зажатым» между ветвью гиперболы и асимптотой — осью 0у);
, но оставаясь всегда выше его (график суммарной функции оказывается как бы «зажатым» между ветвью гиперболы и асимптотой — осью 0у); - при стремлении к нулю справа график функции
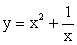 все более приближается к графику функции
все более приближается к графику функции 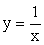 , но оставаясь всегда выше его (ветвь гиперболы оказывается как бы «зажатой» между асимптотой — осью Ох и ветвью графика суммарной функции);
, но оставаясь всегда выше его (ветвь гиперболы оказывается как бы «зажатой» между асимптотой — осью Ох и ветвью графика суммарной функции); - при стремлении к +∞ график функции
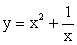 все более приближается к графику функции y = x2, но оставаясь всегда выше его.
все более приближается к графику функции y = x2, но оставаясь всегда выше его.
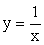 изображен на рисунке:
изображен на рисунке: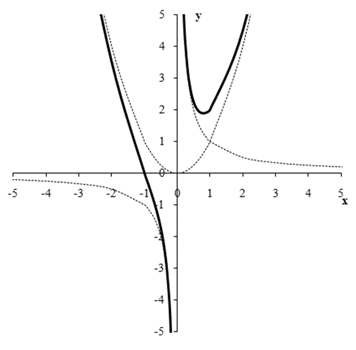
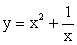
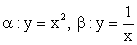 Пример 14.Построим график функции y = sin x + cos x.Прежде всего заметим, что поскольку функции y = sin x и y = cos x — периодические с основным периодом T = 2π, то и функция y = sin x + cos x — периодическая с основным периодом T = 2π. Поэтому построим график функции на отрезке оси 0х длиной в основной период: [-π; π], а затем продолжим его на всю область определения функции. Для построения этого графика используем прием «сложения графиков функций» и будем придерживаться следующего плана.
Пример 14.Построим график функции y = sin x + cos x.Прежде всего заметим, что поскольку функции y = sin x и y = cos x — периодические с основным периодом T = 2π, то и функция y = sin x + cos x — периодическая с основным периодом T = 2π. Поэтому построим график функции на отрезке оси 0х длиной в основной период: [-π; π], а затем продолжим его на всю область определения функции. Для построения этого графика используем прием «сложения графиков функций» и будем придерживаться следующего плана.- Построим график функции y = sin x.
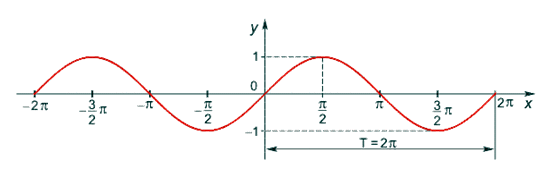
- Построим график функции y = cos x.
- Рассмотрим характерные точки:
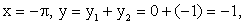
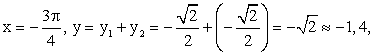
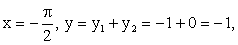
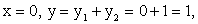
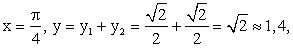
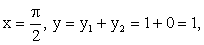
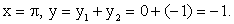
- Рассмотрим также дополнительные точки — точки пересечения графика суммарной функции с осью 0х; для этого решим уравнение sin x + cos x = 0 на отрезке [-π; π]; имеем значения
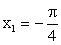 и
и 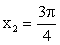 .
.
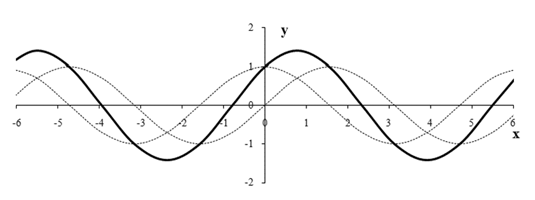
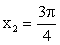 Видеолекция «Функции. Графики элементарных функций»:
Видеолекция «Функции. Графики элементарных функций»: 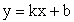 ;
;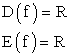
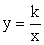 ;
;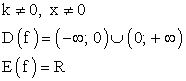
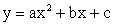 ;
;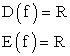
 ;
;
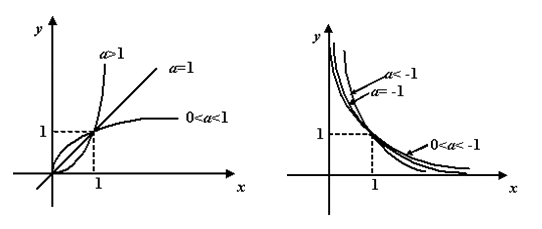
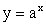 ;
;
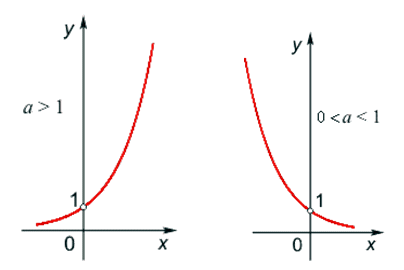
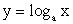 ;
;
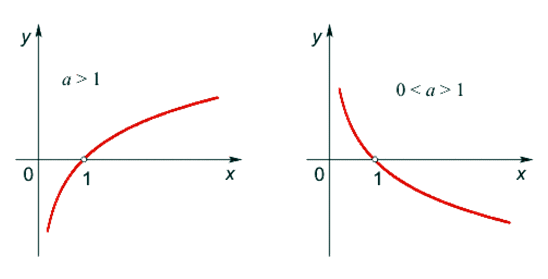
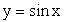
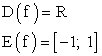
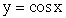
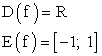
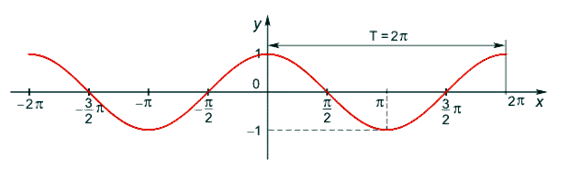
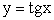
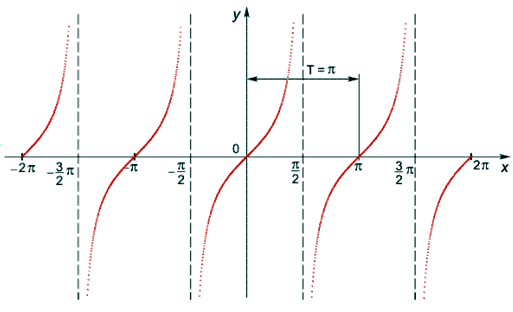
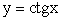
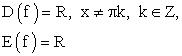
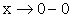 (стремление к нулю слева), то
(стремление к нулю слева), то 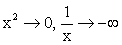 , значит
, значит 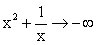 ;
;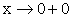 (стремление к нулю справа), то
(стремление к нулю справа), то 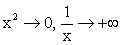 , значит
, значит 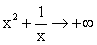 .
.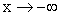 , то
, то 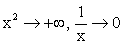 , значит,
, значит, 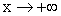 , то
, то 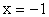 , то
, то 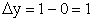 ;
;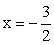 , то
, то 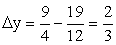 ;
;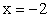 , то
, то 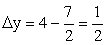 ;
;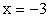 , то
, то 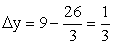 .
.
