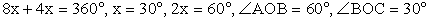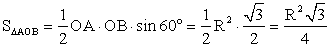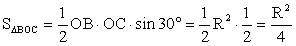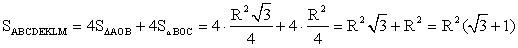Многоугольники. Правильные многоугольники. Вписанные и описанные окружности правильного многоугольника
 .Саму ломаную называют границей многоугольника
.Саму ломаную называют границей многоугольника , а ее внутреннюю область — внутренней областью многоугольника
, а ее внутреннюю область — внутренней областью многоугольника .Звенья границы многоугольника называются сторонами многоугольника
.Звенья границы многоугольника называются сторонами многоугольника , а вершины — вершинами многоугольника
, а вершины — вершинами многоугольника .Отрезок, соединяющий две не соседние вершины многоугольника, называют его диагональю
.Отрезок, соединяющий две не соседние вершины многоугольника, называют его диагональю .Многоугольник называют выпуклым
.Многоугольник называют выпуклым , если он лежит по одну сторону от каждой прямой, содержащей его сторону.Выпуклый многоугольник называется правильным
, если он лежит по одну сторону от каждой прямой, содержащей его сторону.Выпуклый многоугольник называется правильным , если у него все стороны равны и все углы равны.Центром правильного многоугольника
, если у него все стороны равны и все углы равны.Центром правильного многоугольника называется точка, равноудаленная от всех его вершин и всех его сторон.Центральным углом правильного многоугольника
называется точка, равноудаленная от всех его вершин и всех его сторон.Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.Соотношения в многоугольниках:
называется угол, под которым видна сторона из его центра.Соотношения в многоугольниках:- все правильные многоугольники подобны друг другу;
- сумма углов любого выпуклого многоугольника равна 180°(n — 2);
- сумма внешних углов любого выпуклого многоугольника, взятых по одному у каждой вершины, равна 360°;
- периметры подобных многоугольников относятся, как их сходственные стороны, и это отношение равно коэффициенту подобия
 ;
; - площади подобных многоугольников относятся, как квадраты их сходственных сторон, и это отношение равно квадрату коэффициента подобия.
 — окружность, содержащая все вершины многоугольника. Центром является точка (принято обозначать O) пересечения серединных перпендикуляров к сторонам многоугольника (рис. 1
— окружность, содержащая все вершины многоугольника. Центром является точка (принято обозначать O) пересечения серединных перпендикуляров к сторонам многоугольника (рис. 1  ).Как следствие: если рядом с n-угольником описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности).Вокруг любого правильного многоугольника можно описать окружность, и притом только одну.Вписанный простой (без самопересечений) четырехугольник по определению является выпуклым.Вокруг выпуклого четырехугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180°.Можно описать окружность вокруг:
).Как следствие: если рядом с n-угольником описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности).Вокруг любого правильного многоугольника можно описать окружность, и притом только одну.Вписанный простой (без самопересечений) четырехугольник по определению является выпуклым.Вокруг выпуклого четырехугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180°.Можно описать окружность вокруг:- любого прямоугольника (частный случай квадрат);
- любой равнобедренной трапеции.
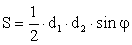 Описанный многоугольник(p — полупериметр; r — радиус вписанной окружности):
Описанный многоугольник(p — полупериметр; r — радиус вписанной окружности):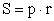 Правильный многоугольник(an — сторона правильного n-угольника; R — радиус описанной окружности; r — радиус вписанной окружности):
Правильный многоугольник(an — сторона правильного n-угольника; R — радиус описанной окружности; r — радиус вписанной окружности):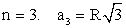
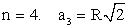
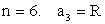
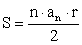 Окружность называется вписанной в выпуклый многоугольник
Окружность называется вписанной в выпуклый многоугольник , если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности
, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности .Радиус вписанной в многоугольник окружности
.Радиус вписанной в многоугольник окружности равен отношению его площади к полупериметру.
равен отношению его площади к полупериметру.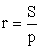 Во всяком описанном четырехугольнике середины диагоналей и центр вписанной окружности лежат на одной прямой (теорема Ньютона
Во всяком описанном четырехугольнике середины диагоналей и центр вписанной окружности лежат на одной прямой (теорема Ньютона ). На ней же лежит середина отрезка с концами в точках пересечения противоположных сторон четырехугольника. Эта прямая называется прямой Гаусса
). На ней же лежит середина отрезка с концами в точках пересечения противоположных сторон четырехугольника. Эта прямая называется прямой Гаусса .Центр вписанной в четырехугольник окружности — точка пересечения высот треугольника с вершинами в точке пересечения диагоналей и точках пересечения противоположных сторон (теорема Брокара
.Центр вписанной в четырехугольник окружности — точка пересечения высот треугольника с вершинами в точке пересечения диагоналей и точках пересечения противоположных сторон (теорема Брокара ).Пример 1.Можно ли в четырехугольник ABCD со сторонами AВ = 7 см, ВC = 9 см, СD = 8 cм, AD = 6 см вписать окружность?
).Пример 1.Можно ли в четырехугольник ABCD со сторонами AВ = 7 см, ВC = 9 см, СD = 8 cм, AD = 6 см вписать окружность?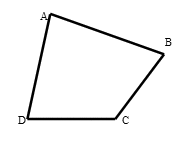 РешениеТак как суммы противоположных сторон равны:AВ + СD = 7 + 8 = 15 cм,BС + AD = 9 + 6 = 15 cм, то в него можно вписать окружность.Ответ: вписать окружность можно.Пример 2.Можно ли вокруг четырехугольник ABCD с углами
РешениеТак как суммы противоположных сторон равны:AВ + СD = 7 + 8 = 15 cм,BС + AD = 9 + 6 = 15 cм, то в него можно вписать окружность.Ответ: вписать окружность можно.Пример 2.Можно ли вокруг четырехугольник ABCD с углами 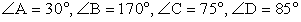 описать окружность?РешениеТак как суммы противоположных углов не равны:
описать окружность?РешениеТак как суммы противоположных углов не равны: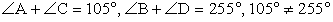 ,то вокруг такого четырехугольника нельзя описать окружность.Ответ: описать окружность нельзя.Пример 3.В равнобедренной трапеции основания 21 и 9 сантиметров, высота — 8 сантиметров. Найти радиус описанной окружности.
,то вокруг такого четырехугольника нельзя описать окружность.Ответ: описать окружность нельзя.Пример 3.В равнобедренной трапеции основания 21 и 9 сантиметров, высота — 8 сантиметров. Найти радиус описанной окружности.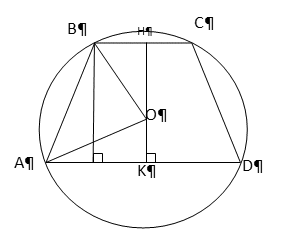 Решение
Решение- Проведем серединные перпендикуляры к основаниям Н и К, тогда центр окружности О лежит на прямой НК.
- АО = ОВ = R. Точка О делит отрезок НК на две части: пусть НО = х, тогда ОК = 8 — х.
- АО2 = АК2 + КО2; ОВ2 = ВН2 + НО2;так как ОА2 = ОВ2, получим:АК2 + КО2 = ВН2 + НО2
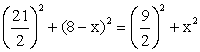
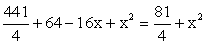
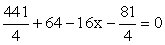
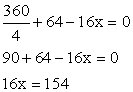
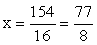
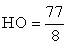
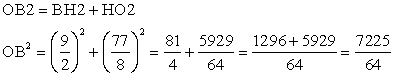
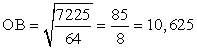
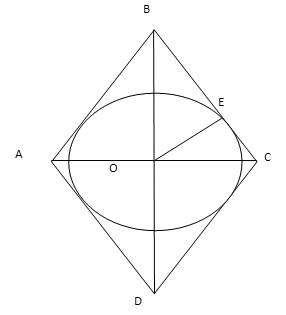 РешениеДано: ромб, радиус вписанной окружности — R, BD > r в 4 раза.Найти: SABCDОтвет:
РешениеДано: ромб, радиус вписанной окружности — R, BD > r в 4 раза.Найти: SABCDОтвет: 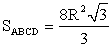 Пример 5.Найдите площадь равнобедренной трапеции, описанной около окружности с радиусом 4, если известно, что боковая сторона трапеции равна 10.
Пример 5.Найдите площадь равнобедренной трапеции, описанной около окружности с радиусом 4, если известно, что боковая сторона трапеции равна 10.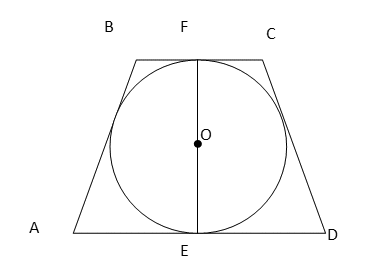 РешениеДано: ABCD — равнобедренная трапеция, r = 4, AB = 10Найти: SABCD
РешениеДано: ABCD — равнобедренная трапеция, r = 4, AB = 10Найти: SABCD- AB = CD = 10 по условию.
- AB + CD = AD + BC по свойству вписанной окружности.
- AD + BC = 10 + 10 = 20.
- FE = 2r = 2 · 4 = 8.
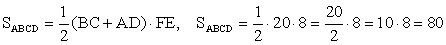
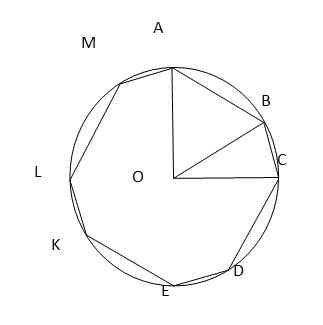 РешениеОтвет:
РешениеОтвет: 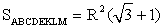 . Видеолекция «Многоугольники. Правильные многоугольники. Вписанные и описанные окружности правильного многоугольника»:
. Видеолекция «Многоугольники. Правильные многоугольники. Вписанные и описанные окружности правильного многоугольника»: 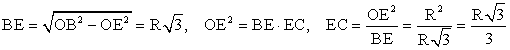
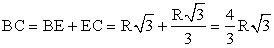
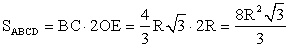
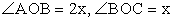 , тогда по условию
, тогда по условию