 . Любое натуральное число в десятичной системе счисления записывают с помощью цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.Например: 2457 = 21000+4100+510+7.Вообще, если a - цифра тысяч, b - цифра сотен, c - цифра десятков, d - цифра единиц, то имеем такую запись:
. Любое натуральное число в десятичной системе счисления записывают с помощью цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.Например: 2457 = 21000+4100+510+7.Вообще, если a - цифра тысяч, b - цифра сотен, c - цифра десятков, d - цифра единиц, то имеем такую запись: =
= .Напомним основные определения.Пусть m, n, k натуральные числа.
.Напомним основные определения.Пусть m, n, k натуральные числа.- 1) m + n = k , m – первое слагаемое, n – второе слагаемое, k – сумма.2) m - n = k, m - уменьшаемое, n - вычитаемое, k – разность.3) m * n = k, m – первый множитель, n – второй множитель, k – произведение.4) m : n = k говорят, что m - делимое, n - делитель, k - частное.5)
 , m - основание степени, n – показатель степени, k – степень.6)
, m - основание степени, n – показатель степени, k – степень.6)  , m – подкоренное число, n – показатель корня, k – корень.
, m – подкоренное число, n – показатель корня, k – корень.- a + b = b + a - переместительное свойство сложения
- (a + b) + c = a + (b +c) - сочетательное свойство сложения
- ab = ba - переместительное свойство умножения
- (ab)c = a(bc) - сочетательное свойство умножения
- a(b + c) = ab + ac - распределительное свойство умножения относительно сложения
 . При этом число n считается отличным от нуля и говорят:
«m кратно n»
.Число 1 является делителем любого целого числа. Число 0 делится на любое число, в том числе и на ноль, но ни одно целое число, отличное от нуля, не делится на 0.Например, положительными делителями числа 132 являются числа 1, 2, 3, 4, 6, 11,12, 22, 33, 44, 66, 132.Вместо слов «m делится на n» можно сказать «n делит m». Для такого высказывания применяется стандартное обозначение n | m. Однако оно не очень удобно, потому что привычнее говорить «m делится на n», что часто обозначают как
. При этом число n считается отличным от нуля и говорят:
«m кратно n»
.Число 1 является делителем любого целого числа. Число 0 делится на любое число, в том числе и на ноль, но ни одно целое число, отличное от нуля, не делится на 0.Например, положительными делителями числа 132 являются числа 1, 2, 3, 4, 6, 11,12, 22, 33, 44, 66, 132.Вместо слов «m делится на n» можно сказать «n делит m». Для такого высказывания применяется стандартное обозначение n | m. Однако оно не очень удобно, потому что привычнее говорить «m делится на n», что часто обозначают как 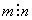 .Отношение делимости обладает следующими свойствами:
.Отношение делимости обладает следующими свойствами:- 1) Если два числа делятся на n, то и их сумма делится на n:
 .2) Если число m делится на n, то и число mk при любом k делится на n:
.2) Если число m делится на n, то и число mk при любом k делится на n: , где k - любое число3) Если m делится на n, а n делится на k, то m делится на k:
, где k - любое число3) Если m делится на n, а n делится на k, то m делится на k: .
.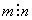 и
и  означают, что существуют числа
означают, что существуют числа  и
и  такие, что
такие, что  ,
,  .Сложим эти два равенства:
.Сложим эти два равенства:  .Равенство
.Равенство  означает по определению делимости, что m + n делится на n.Два других свойства доказываются аналогично.На основе свойств делимости выводятся признаки делимости.Признаки делимости натуральных чисел
означает по определению делимости, что m + n делится на n.Два других свойства доказываются аналогично.На основе свойств делимости выводятся признаки делимости.Признаки делимости натуральных чисел- Если каждое слагаемое делится на некоторое число, то и сумма делится на это число.
- Если в произведении хотя бы один из множителей делится на некоторое число, то и произведение делится на это число.
- Натуральное число делится на 2 тогда и только тогда, когда последняя цифра делится на 2.
- Натуральное число делится на 5 тогда и только тогда, когда его последняя цифра либо 0, либо 5.
- Натуральное число делится на 10 тогда и только тогда, когда его последняя цифра 0.
- Натуральное число, содержащее не менее трех цифр, делится на 4 тогда и только тогда, когда делится на 4 двузначное число, образованное последними двумя цифрами заданного числа.
- Натуральное число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3.
- Натуральное число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.
На 2 |
Числа, оканчивающиеся нулем или четной цифрой |
…….8 |
На 3 |
Числа, сумма цифр которых делится на 3 |
46215 |
На 4 |
Числа, у которых две последние цифры нули или образуют число, делящееся на 4 |
……16 |
На 5 |
Числа, оканчивающиеся нулем или цифрой 5 |
……5 |
На 6 |
Числа, одновременно делящиеся на 3 и на 2 |
126 |
На 8 |
Числа, у которых три последние цифры нули или образуют число, делящееся на 8 |
…..120 |
На 9 |
Числа, сумма цифр которых делятся на 9 |
37683 |
На 10 |
Числа, у которых последняя цифра 0 |
….0 |
На 25 |
Числа, две последние цифры которых нули или образуют число, делящееся на 25 |
…….75 |
На 16, 32 |
Числа, у которых три последние цифры нули или образуют число, делящееся на 16 (32 соответственно) |
…….48 |
 =a5 105 + a4104 + ... + a110 + a0 = 100 (a51000 + a4100 + a310 + a2)+ a110 + a0.Первое из чисел делится на 4, так как 100 делится на 4.Значит, всё число делится на 4 тогда и только тогда, когда 10a1 + a0 делится на 4.Деление с остаткомЕсли натуральное число m не делится на натуральное число n, т.е. не существует такого натурального числа k, что m = nk, то деление называется с остатком
=a5 105 + a4104 + ... + a110 + a0 = 100 (a51000 + a4100 + a310 + a2)+ a110 + a0.Первое из чисел делится на 4, так как 100 делится на 4.Значит, всё число делится на 4 тогда и только тогда, когда 10a1 + a0 делится на 4.Деление с остаткомЕсли натуральное число m не делится на натуральное число n, т.е. не существует такого натурального числа k, что m = nk, то деление называется с остатком .Формула деления с остатком: m = nk + r, где m - делимое, n - делитель, k - частное, r - остаток, причем 0
.Формула деления с остатком: m = nk + r, где m - делимое, n - делитель, k - частное, r - остаток, причем 0 r<
n.
r<
n.- Любое число можно представить в виде: m = 2k + r , где остаток r = 0 или r = 1
- Любое число можно представить в виде: m = 4k + r , где остаток r = 0 или r = 1 или r = 2 или r = 3
- Любое число можно представить в виде: m = nk + r, где остаток r принимает значения от 0 до n – 1.
- a) 124857408;b) 5741996;c) 3412701;d) 24589144.
 4, поскольку число, образованное двумя последними цифрами 44 делится на 4. Следующее число, которое мы рассмотрим, 3412701. Это число нечетное, поэтому оно не делится на четные числа, также к нему не подходят признак делимости на 5, а следовательно, проверяем делимость на 3 и 9. Находим сумму чисел 3+4+1+2+7+0+1= 18. Делаем вывод, что 3412701
4, поскольку число, образованное двумя последними цифрами 44 делится на 4. Следующее число, которое мы рассмотрим, 3412701. Это число нечетное, поэтому оно не делится на четные числа, также к нему не подходят признак делимости на 5, а следовательно, проверяем делимость на 3 и 9. Находим сумму чисел 3+4+1+2+7+0+1= 18. Делаем вывод, что 3412701 3 или 9. У числа 5741996 две последние цифры образуют число 96, которое делится на 4 и 32, следовательно, 5741996
3 или 9. У числа 5741996 две последние цифры образуют число 96, которое делится на 4 и 32, следовательно, 5741996 4 и 32. Число 124857408 не кратно 4 и 32. Проверяем делимость этого числа на 8: последние три цифры этого числа образуют число 408, которое делится 8. Заключаем, что 124857408
4 и 32. Число 124857408 не кратно 4 и 32. Проверяем делимость этого числа на 8: последние три цифры этого числа образуют число 408, которое делится 8. Заключаем, что 124857408 8.Натуральные числа делятся на простые и составные. Простые
8.Натуральные числа делятся на простые и составные. Простые это те натуральные числа, которые имеет только два делителя (само число и единица). Натуральное число называется составным
это те натуральные числа, которые имеет только два делителя (само число и единица). Натуральное число называется составным , если имеет более двух делителей.Простых чисел – бесконечное множество. Простые числа, не превосходящие 200 представлены в таблице.
, если имеет более двух делителей.Простых чисел – бесконечное множество. Простые числа, не превосходящие 200 представлены в таблице.
Таблица простых чисел
2 |
3 |
5 |
7 |
11 |
13 |
17 |
19 |
23 |
29 |
31 |
37 |
41 |
43 |
47 |
53 |
59 |
61 |
67 |
71 |
73 |
79 |
83 |
89 |
97 |
101 |
103 |
107 |
109 |
113 |
127 |
131 |
137 |
139 |
149 |
151 |
157 |
163 |
167 |
173 |
179 |
181 |
191 |
193 |
197 |
199 |
|
|
270 |
2 |
135 |
5 |
27 |
3 |
9 |
3 |
3 |
3 |
1 |
|
 чисел 48 и 60, наибольшее среди них число 12 называется наибольшим общим делителем
чисел 48 и 60, наибольшее среди них число 12 называется наибольшим общим делителем .Замечание. Для того чтобы выписать все делители, надо узнать сколько их всего будет у данного числа. Для этого надо разложить число 48 на простые множители: 48=3*2*2*2*2= 3*24. Для определения числа делителей числа 48 необходимо к степени каждого множителя прибавить единицу и полученные суммы перемножить, т.е. (1+1)*(4+1)=2*5=10. Что подтверждается предыдущими вычислениями.Для любых заданных натуральных чисел a и b можно найти наибольший общий делитель. Он обозначается HOD(a,b) и читается:
«HOD от a и b»
. Например, HOD(a,b) = HOD(48,60) = 12.Взаимно простые числа. Если числа a и b таковы, что HOD(a, b) = 1, то такие числа называют взаимно простые
.Замечание. Для того чтобы выписать все делители, надо узнать сколько их всего будет у данного числа. Для этого надо разложить число 48 на простые множители: 48=3*2*2*2*2= 3*24. Для определения числа делителей числа 48 необходимо к степени каждого множителя прибавить единицу и полученные суммы перемножить, т.е. (1+1)*(4+1)=2*5=10. Что подтверждается предыдущими вычислениями.Для любых заданных натуральных чисел a и b можно найти наибольший общий делитель. Он обозначается HOD(a,b) и читается:
«HOD от a и b»
. Например, HOD(a,b) = HOD(48,60) = 12.Взаимно простые числа. Если числа a и b таковы, что HOD(a, b) = 1, то такие числа называют взаимно простые .Пример: Числа 26 и 35 являются взаимно простыми, хотя сами они составные. Так как 26=2*13 и 35=5*7 , то HOD(26,35) = 1.Чтобы найти наибольший общий делитель нескольких чисел, надо разложить их на простые множители, найти общие простые множители и вычислить произведение общих простых множителей, взяв каждый из них с наименьшим, из имеющихся, показателем.Пример: Найти HOD(56,84,96)Решение: 56=2*2*2*7=7*2396=2*2*2*2*2*7=7*2584=2*2*3*7=7*3*22и тогда HOD(56,84,96) = 7*22 = 4*7=28.Пусть даны числа 12 и 16.Выпишем все числа, кратные числа 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120. Также выпишем все числа, кратные числа 16: 16, 32, 48, 64, 80, 96, 112, 128. Среди выписанных чисел есть одинаковые: 48 и 96.Все эти числа называются общими кратными
.Пример: Числа 26 и 35 являются взаимно простыми, хотя сами они составные. Так как 26=2*13 и 35=5*7 , то HOD(26,35) = 1.Чтобы найти наибольший общий делитель нескольких чисел, надо разложить их на простые множители, найти общие простые множители и вычислить произведение общих простых множителей, взяв каждый из них с наименьшим, из имеющихся, показателем.Пример: Найти HOD(56,84,96)Решение: 56=2*2*2*7=7*2396=2*2*2*2*2*7=7*2584=2*2*3*7=7*3*22и тогда HOD(56,84,96) = 7*22 = 4*7=28.Пусть даны числа 12 и 16.Выпишем все числа, кратные числа 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120. Также выпишем все числа, кратные числа 16: 16, 32, 48, 64, 80, 96, 112, 128. Среди выписанных чисел есть одинаковые: 48 и 96.Все эти числа называются общими кратными чисел 14 и 12, наименьшее среди них число 48 называется наименьшим общим кратным чисел
чисел 14 и 12, наименьшее среди них число 48 называется наименьшим общим кратным чисел 14 и 12.Для любых заданных натуральных чисел a и b можно найти наименьшее общее кратное. Он обозначается HOK(a,b) и читается:
«HOK от a и b»
. Например, HOK(a,b) = HOK(14,12) = 48.Замечание. Любое общее кратное чисел a и b делится на HOK(a,b).Чтобы найти наименьшее общее кратное нескольких чисел, надо разложить их на простые множители и вычислить произведение всех простых множителей, взяв каждый из них с наибольшим из имеющихся показателем степени.Пример: Найти HOK(56,84,96)Решение: 56=2*2*2*7=7*23.96=2*2*2*2*2*7=7*25.84=2*2*3*7=7*3*22.и тогда HOK(56,84,96) = 7*3*25= 672.Теорема. Для любых натуральных чисел a и b справедливо равенство =ab. Если числа a и b взаимно простые, т.е. HOD(a,b) = 1, то HOK(a,b) = ab.Наименьшее общее кратное двух взаимно простых чисел равно произведению этих чисел.Свойства наибольшего общего делителя и наименьшего общего кратного нескольких натуральных чиселСвойство 1. HOD(a,b,c)=HOD(HOD(a,b)c).Свойство 2. HOK(a,b,c)=HOK(HOK(a,b)c).Свойство 3. HOD(ac,bc)=c*HOD(a,b).Свойство 4. HOK(ac,bc)=c*HOK(a,b).Свойство 5. HOD(n,n+1n+2)=1.Свойство 6. Числа a*HOD(a,b) и b*HOD(a,b) - взаимно простые.Свойство 7. HOD(n,n+k)=HOD(n,k)=1.Свойство 8. HOK(a,b)=ab*HOD(a,b).Пример 1: HOD(3n,6n+3)=3*HOD(n,2n+1)=3*HOD(n, n+(n+1))=3*HOD(n,n+1)=3.Пример 2: HOD(30n+25, 20n+15)=5*HOD(6n+5, 4n+3)=5*HOD(4n+3+(2n+2), 4n+3)= 5*HOD(2n+2, 4n+3)=5*HOD(2n+2, 2n+2+2n+1)=5*HOD(2n+2, 2n+1)=5*1=5. Видеолекция «Натуральные числа»:
14 и 12.Для любых заданных натуральных чисел a и b можно найти наименьшее общее кратное. Он обозначается HOK(a,b) и читается:
«HOK от a и b»
. Например, HOK(a,b) = HOK(14,12) = 48.Замечание. Любое общее кратное чисел a и b делится на HOK(a,b).Чтобы найти наименьшее общее кратное нескольких чисел, надо разложить их на простые множители и вычислить произведение всех простых множителей, взяв каждый из них с наибольшим из имеющихся показателем степени.Пример: Найти HOK(56,84,96)Решение: 56=2*2*2*7=7*23.96=2*2*2*2*2*7=7*25.84=2*2*3*7=7*3*22.и тогда HOK(56,84,96) = 7*3*25= 672.Теорема. Для любых натуральных чисел a и b справедливо равенство =ab. Если числа a и b взаимно простые, т.е. HOD(a,b) = 1, то HOK(a,b) = ab.Наименьшее общее кратное двух взаимно простых чисел равно произведению этих чисел.Свойства наибольшего общего делителя и наименьшего общего кратного нескольких натуральных чиселСвойство 1. HOD(a,b,c)=HOD(HOD(a,b)c).Свойство 2. HOK(a,b,c)=HOK(HOK(a,b)c).Свойство 3. HOD(ac,bc)=c*HOD(a,b).Свойство 4. HOK(ac,bc)=c*HOK(a,b).Свойство 5. HOD(n,n+1n+2)=1.Свойство 6. Числа a*HOD(a,b) и b*HOD(a,b) - взаимно простые.Свойство 7. HOD(n,n+k)=HOD(n,k)=1.Свойство 8. HOK(a,b)=ab*HOD(a,b).Пример 1: HOD(3n,6n+3)=3*HOD(n,2n+1)=3*HOD(n, n+(n+1))=3*HOD(n,n+1)=3.Пример 2: HOD(30n+25, 20n+15)=5*HOD(6n+5, 4n+3)=5*HOD(4n+3+(2n+2), 4n+3)= 5*HOD(2n+2, 4n+3)=5*HOD(2n+2, 2n+2+2n+1)=5*HOD(2n+2, 2n+1)=5*1=5. Видеолекция «Натуральные числа»: 
