Объем куба, прямоугольного параллелепипеда, пирамиды, призмы
— величина, сопоставляющая фигурам в пространстве неотрицательные действительные числа. За единицу объема принимается куб, ребро которого равно единице измерения длины.Для объемов пространственных фигур справедливы свойства:- Объем фигуры в пространстве является неотрицательным числом.
- Равные фигуры имеют равные объемы.
- Если фигура Ф составлена из двух неперекрывающихся фигур Ф1 и Ф2, то объем фигуры Ф равен сумме объемов фигур Ф1 и Ф2, т.е.V(Ф)=V(Ф1) + V(Ф2).
.Основные формулы- Произвольная призма (Pсеч , Sсеч — периметр и площадь перпендикулярного сечения, l — боковое ребро, Н — высота):Sб = Pсеч ·l, V = Sосн ·H, V = Sсеч ·l
- Прямая призма:Sпп = Sбок + 2Sосн , Sбок = P·H, Sполн = Sбок + 2Sосн , V = Sосн. H
- Прямоугольный параллелепипед (a, b, c — его измерения, d — диагональ):Sб = Рсеч·Н, Sполн = 2(ab + ac + bc)V = Sосн ·H, V = abc, d2 = a2 + b2 + c2.
- Куб: V = a3, Sполн = 6а2.
- Произвольная пирамида (Si — площади боковых граней, S — площадь основания и h — высота; P — периметр основания, l — боковое ребро):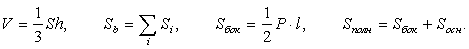
- Правильная пирамида (P — периметр основания, Н — высота, hбок — апофема )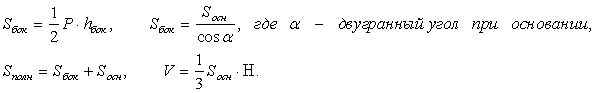
- Произвольная усеченная пирамида:
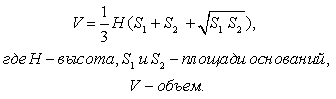
- Правильная усеченная пирамида:
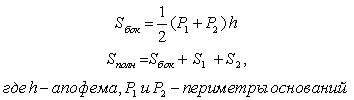
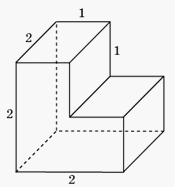Решение 1.Многогранник состоит из двух прямоугольных параллелепипедов, объемы которых равны 2·1·1 = 2 и 2·2·1 = 4. Следовательно, объем многогранника равен 2 + 4 = 6.Решение 2.Многогранник получается из куба, объем которого равен 23 = 8, вырезанием прямоугольного параллелепипеда, объем которого равен 2·1·1 = 2. Следовательно, объем многогранника равен 8 – 2 = 6.Ответ: 6.Пример 2.Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
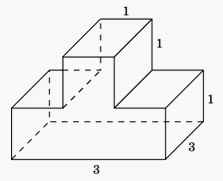Решение.Многогранник составлен из двух прямоугольных параллелепипедов, объемы которых равны 3·3·1 = 9 и 3·1·1 = 3. Следовательно, объем многогранника равен 9 + 3 = 12.Ответ: 12.Пример 3.Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
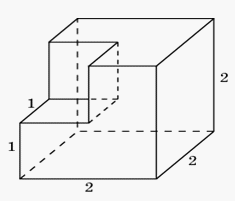Решение.Многогранник получается из куба, объем которого равен 8, вырезанием куба, объем которого равен 1. Следовательно, объем многогранника равен 7.Ответ: 7.Пример 4.Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
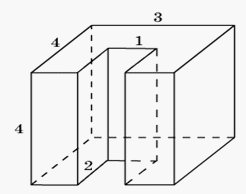Решение.Многогранник получается из прямоугольного параллелепипеда, объем которого равен 4·4·3 = 48, вырезанием прямоугольного параллелепипеда, объем которого равен 4·2·1 = 8. Следовательно, объем многогранника равен 48 – 8 = 40.Ответ: 40.Пример 5.Площадь полной поверхности куба равна 24 см2 . Найдите его объем.Решение.Поскольку куб имеет шесть одинаковых граней, найдем площадь одной из них: 24 / 6 = 4 см2.Зная площадь грани куба, найдем величину ребра a = 
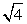= 2 см.Тогда его объем равен V = a3 = 23 = 8 см3 .Ответ: 8.Пример 6.В прямоугольном параллелепипеде ребра изменены следующим образом: длина и ширина увеличены в 2 раза, высота уменьшена в 6 раз. Как изменится площадь его боковой поверхности и объем при заданном изменении.Решение.Пусть измерения параллелепипеда а, b, c. Тогда его площадь боковой поверхности Sб = Росн·h = 2c(a + b). Проследим, как изменится площадь боковой поверхности при заданном в задаче преобразовании: 
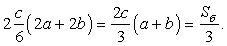Таким образом, площадь боковой поверхности прямоугольного параллелепипеда уменьшилась в три раза.До преобразования объем был равен V = abc. После преобразования получаем 
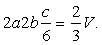Следовательно, объем новой фигуры составляет 2/3 от объема начальной фигуры.Ответ: площадь боковой поверхности прямоугольного параллелепипеда уменьшилась в 3 раза; объем прямоугольного параллелепипеда уменьшился в 2/3 раза.Пример 7.Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол в 60° и равно 2. Найдите объем параллелепипеда.Решение.
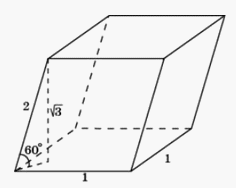Площадь грани параллелепипеда, являющейся ромбом со стороной 1 и острым углом 60°, равна 
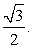Высота, опущенная на эту грань, равна 
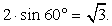Объем параллелепипеда равен 1,5.Ответ: 1,5.ПризмаПример 8.Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.Решение.
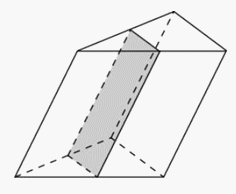Площадь основания отсеченной призмы равна четверти площади основания исходной призмы. Высота отсеченной призмы равна высоте исходной призмы. Следовательно, объем отсеченной призмы равен четверти объема исходной призмы, т.е. равен 8.Ответ: 8.Пример 9.Пусть Q — площадь одной из боковых граней треугольной призмы, d — расстояние от противоположного ребра до этой грани. Тогда объем этой призмы можно найти по формуле: V = 1/2Qd.
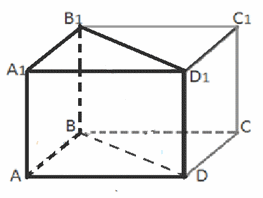Доказательство:Пусть площадь грани АА1D1D равна Q, а расстояние от ВВ1 до этой грани равно d. Объем параллелепипеда ABCDA1B1C1D1 равенVп-да = Qd. Так как объем параллелепипеда в 2 раза больше объема призмы ABDA1B1D1 , то объем этой призмы: V = 1/2Qd.
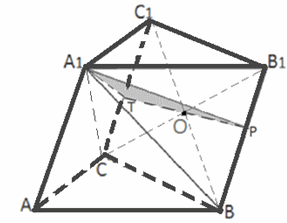Пример 10.Все ребра призмы ABCA1B1C1 равны между собой. Углы ВАА1 и САА1 равны по 60°.Найти объем призмы , если площадь грани АВВ1А1 равна 8
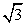.Решение.Так как все ребра равны, то все боковые грани призмы — ромбы, а основания — правильные треугольники. Боковые грани АВВ1А1 и АСС1 А1 – ромбы с углом 60°, поэтому обозначим ВА1 = СА1 = СВ1 = х.Площадь грани АВВ1А1 равна S = х2sin60 = х2 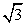/ 2. Из условия получаем уравнение: х2 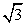/ 2 = 8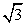
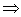х2 =16 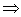х = 4.Объем призмы найдем по формуле:
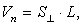где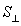 
— площадь перпендикулярного сечения, L — длина бокового ребра.Построим перпендикулярное сечение А1РТ, где Р и Т — середины ребер ВВ1 и СС1 соответственно. Так как треугольники А1ВВ1 и А1СС1 правильные, то их медианы являются высотами, поэтому А1Р 
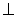ВВ1, А1Т 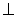СС1. Отсюда по признаку перпендикулярности прямой и плоскости все боковые ребра призмы перпендикулярны плоскости А1РТ, т.е. А1РТ — перпендикулярное сечение данной призмы. В 
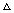А1РТ: А1О РТ, РТ = х = 4, А1Р = х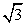 / 2,
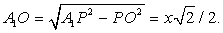.Следовательно, площадь перпендикулярного сечения SA1PT = 1/2РТ·А1О = х2
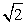/ 2.Тогда объем призмы V = SA1PT·AA1 = х3 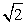/ 4 = 43 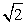/ 4 = 16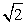.Ответ: 16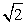.ПирамидаПример 11.Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?Решение.
Воспользуемся тем, что если два тетраэдра подобны и коэффициент подобия равен k, то отношение объемов этих тетраэдров равно k3. Если ребра тетраэдра увеличить в два раза, то объем тетраэдра увеличится в 8 раз.Ответ: 8.Пример 12.Найти объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3.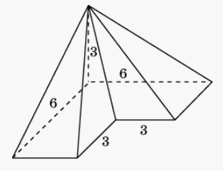
Решение.Площадь основания пирамиды равна 36 – 9 = 27, высота равна 3. Следовательно, объем пирамиды равен V = 27·3/3 = 27.Ответ: 27.Пример 13.Найти объем правильного тетраэдра, все ребра которого равны b.Решение.
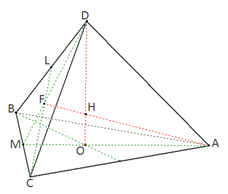DO = h — высота тетраэдра.
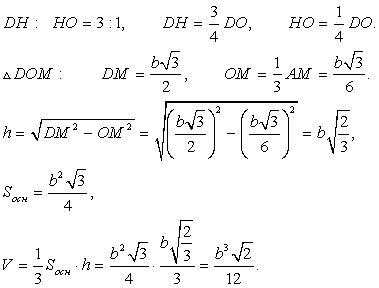Ответ: 
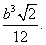Пример 14.В правильной треугольной пирамиде боковые грани наклонены к основанию под углом 60 градусов. Расстояние от центра основания до боковой грани равно 2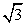. Найти объём пирамиды.Решение.
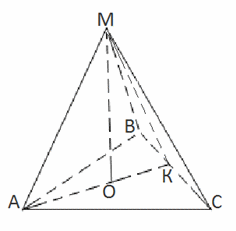Основанием правильной треугольной пирамиды по определению является равносторонний треугольник. А расстояние от центра основания до боковой грани равно радиусу вписанной окружности. Площадь равностороннего треугольника равна:
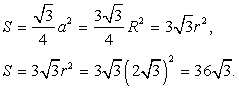Поскольку грани наклонены к основанию под углом 60 градусов, то для прямоугольного треугольника MOK:tg MKO = MO/KO; tg 60 = MO / (2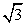) ; 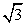= MO / (2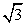); MO = 6 см — высота пирамиды. Объем пирамиды найдем по формуле: S = 1/3 S·h; S = 1/3·36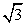·6 ; S = 72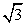Ответ: 72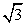.Пример 15.Найти объем пирамиды, все грани которой равнобедренные треугольники с боковой стороной, равной 5, и основанием — 6.Решение.Пусть в пирамиде основанием является 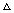АВС, в котором АВ=АС=5, ВС = 6. По теореме косинусов АВ2 + АС2 – ВС2 = 50 - 36 > 0, поэтому 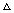АВС — остроугольный. Если AD = 5, то DC = 6, что противоречит условию, поскольку грань ВСD не будет равнобедренным треугольником со сторонами 5, 5, 6. Следовательно, AD = 6, тогда DC = DВ = 5. Сделаем рисунок.
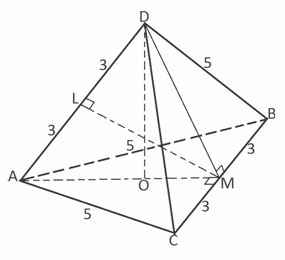Пусть М и L — середины ребер ВС и AD соответственно. Тогда АМ и DМ — медианы в равных равнобедренных треугольниках с общим основанием ВС, проведенные к этому основанию. Следовательно, DМ 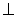ВС, АМ 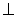ВС и АМ = DМ.По теореме Пифагора из 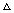АМС: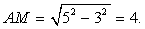 
Значит, АМ = DМ =4.Отсюда следует, что 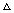АDМ — равнобедренный и его медиана МL — общий перпендикуляр к двум скрещивающимся прямым ВС и AD и , следовательно, его длина — расстояние между прямыми ВС и AD.Кроме того по признаку перпендикулярности плоскостей, АВС 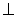АDМ, и , следовательно, высота DО 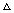АDМ будет являться высотой пирамиды.Из прямоугольного АМL: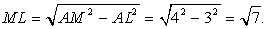 
Высоты треугольника обратно пропорциональны сторонам, к которым они проведены. Следовательно, МL· AD = DО· АМ, 
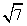·6 = DО·4, DО = 3 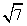/ 2.Площадь основания SABC равна удвоенной площади 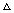АМС и равнаSABC = 2SAMC = 2·1/2·АМ·МС = 4·3 = 12.V = 1/3 · SABC · DО = 12·3 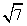/ (2·3) = 6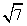.Ответ: 6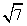.Пример 16.Пусть a и b — длины двух противоположных ребер тетраэдра, d — расстояние между ними, 
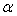— угол между ними. Тогда объем тетраэдра можно вычислить по формуле: V = 1/6 abd·sin.
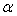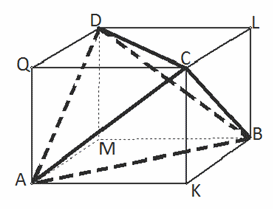Доказательство:Достроим данный тетраэдр АВСD до параллелепипеда АКВМQCLD, проводя через каждое ребро плоскость, параллельную противоположному ребру. Пусть АВ = a, CD = b, тогда площади граней АКВМ и LCQD равны S = 1/2·ab·sin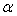. Расстояние между ними d. Тогда объем параллелепипеда равен: Vп-да =1/2· abd·sin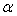. Объем пирамиды составляет 1/3 от объема параллелепипеда, т.е.V = 1/6 abd·sin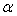.Список используемой литературы Видеолекция «Объемы многогранников»: 
