Шар и сфера
. Поверхность, образуемая при этом, называется сферой.Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки.Эта точка называется центром шара, а данное расстояние называется радиусом шара.Граница шара называется шаровой поверхностью или сферой.Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, называется радиусом.Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром.Концы любого диаметра называются диаметрально противоположными точками шара.Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра на секущую плоскость.Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы — большой окружностью.Любая диаметральная плоскость шара являются его плоскостью симметрии. Центр шара является его центром симметрии.Плоскость, проходящая через точку шаровой поверхности и перпендикулярная радиусу, проведенному в эту точку, называется касательной плоскостью. Данная точка называется точкой касания.Касательная плоскость имеет с шаром только одну общую точку — точку касания.Прямая, проходящая через заданную точку шаровой поверхности перпендикулярно к радиусу, проведенному в эту точку, называется касательной.Через любую точку шаровой поверхности проходит бесконечно много касательных, причем все они лежат в касательной плоскости шара.Шаровым сегментом называется часть шара, отсекаемая от него плоскостью.Шаровым слоем называется часть шара, расположенная между двумя параллельными плоскостями, пересекающими шар.Шаровой сектор получается из шарового сегмента и конуса.Если шаровой сегмент меньше полушара, то шаровой сегмент дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента.Если же сегмент больше полушара, то указанный конус из него удаляется.Основные формулы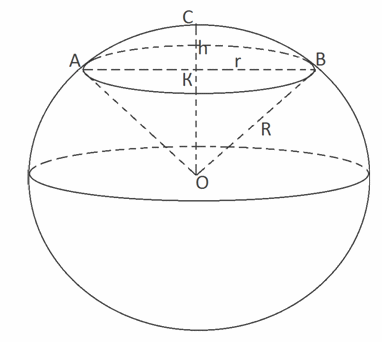
Шар (R = ОВ — радиус):Sб = 4πR2; V = 4πR3 / 3.Шаровой сегмент (R = ОВ — радиус шара, h = СК — высота сегмента, r = КВ — радиус основания сегмента):Vсегм = πh2(R — h / 3)или Vсегм = πh(h2 + 3r2) / 6;Sсегм = 2πRh.Шаровой сектор (R = ОВ — радиус шара, h = СК — высота сегмента):V = Vсегм ± Vкон, «+» — если сегмент меньше,«—» — если сегмент больше полусферы.
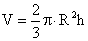или V = Vсегм + Vкон = πh2(R — h / 3) + πr2(R — h) / 3.Шаровой слой (R1 и R2 — радиусы оснований шарового слоя; h = СК — высота шарового слоя или расстояние между основаниями):Vш/сл = πh3 / 6 + πh(R12 + R22) / 2;Sш/сл = 2πRh.Пример 1.Объем шара равен 288π см3. Найти диаметр шара.РешениеV = πd3 / 6288π = πd3 / 6πd3 = 1728πd3 = 1728d = 12 см.Ответ: 12.Пример 2.Три равных сферы радиусом r касаются друг друга и некоторой плоскости. Определить радиус четвертой сферы, касающейся трех данных и данной плоскости.Решение
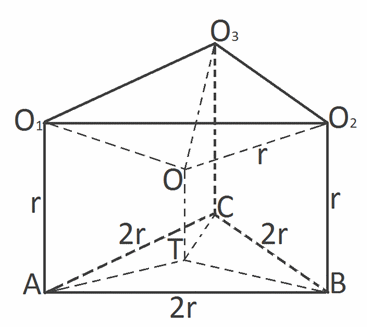Пусть О1, О2, О3 — центры данных сфер и О — центр четвертой сферы, касающейся трех данных и данной плоскости. Пусть А, В, С, Т — точки касания сфер с данной плоскостью. Точки касания двух сфер лежат на линии центров этих сфер, поэтому О1О2 = О2О3 = О3О1 = 2r. Точки равноудалены от плоскости АВС, поэтому АВО2О1, АВО2О3, АВО3О1 — равные прямоугольники, следовательно, ∆АВС — равносторонний со стороной 2r.Пусть х — искомый радиус четвертой сферы. Тогда ОТ = х. Следовательно, 
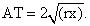Аналогично 
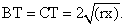Значит, Т — центр равностороннего треугольника. Поэтому 
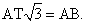Отсюда
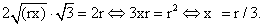Ответ: r / 3.Сфера, вписанная в пирамидуВ каждую правильную пирамиду можно вписать сферу. Центр сферы лежит на высоте пирамиды в точке ее пересечения с биссектрисой линейного угла при ребре основания пирамиды.Замечание. Если в пирамиду, необязательно правильную, можно вписать сферу, то радиус r этой сферы можно вычислить по формуле r = 3V / Sпп, где V — объем пирамиды, Sпп — площадь ее полной поверхности.Пример 3.Коническая воронка, радиус основания которой R, а высота H, наполнена водой. В воронку опущен тяжелый шар. Каким должен быть радиус шара, чтобы объем воды, вытесненный из воронки погруженной частью шара, был максимальным?РешениеПроведем сечение через центр конуса. Данное сечение образует равнобедренный треугольник.
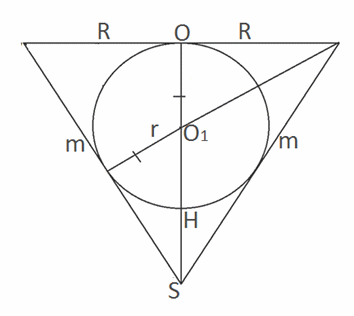Если в воронке находится шар, то максимальный размер его радиуса будет равен радиусу вписанной в получившийся равнобедренный треугольник окружности.Радиус вписанной в треугольник окружности равен:r = S / p, где S — площадь треугольника, p — его полупериметр.Площадь равнобедренного треугольника равна половине высоты (H = SO), умноженной на основание. Но поскольку основание — удвоенный радиус конуса, то S = RH.Полупериметр равен p = 1/2 (2R + 2m) = R + m.m — длина каждой из равных сторон равнобедренного треугольника;R — радиус окружности, составляющей основание конуса.Найдем m по теореме Пифагора: 
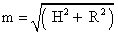, откуда
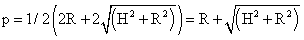Кратко это выглядит следующим образом: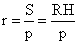
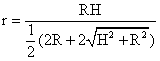
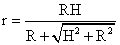Ответ: 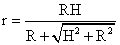Пример 4.В правильной треугольной пирамиде с двугранным углом при основании, равным α, расположены два шара. Первый шар касается всех граней пирамиды, а второй шар касается всех боковых граней пирамиды и первого шара. Найти отношение радиуса первого шара к радиусу второго шара, если tgα = 24/7.Решение
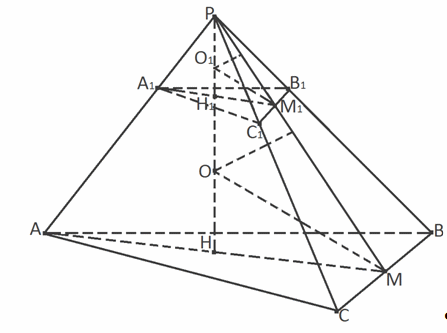Пусть РАВС — правильная пирамида и точка Н — центр ее основания АВС. Пусть М — середина ребра ВС. Тогда 
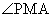— линейный угол двугранного угла 
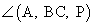, который по условию равен α, причем α < 90°. Центр первого шара, касающегося всех граней пирамиды, лежит на отрезке РН в точке его пересечения с биссектрисой 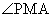.Пусть НН1 — диаметр первого шара и плоскость, проходящая через точку Н1 перпендикулярно прямой РН, пересекает боковые ребра РА, РВ, РС соответственно в точках А1, В1, С1. Тогда Н1 будет центром правильного ∆А1В1С1, а пирамида РА1В1С1 будет подобна пирамиде РАВС с коэффициентом подобия k = РН1 / РН. Заметим, что второй шар, с центром в точке О1, является вписанным в пирамиду РА1В1С1 и поэтому отношение радиусов вписанных шаров равно коэффициенту подобия: ОН / ОН1 = РН / РН1. Из равенства tgα = 24/7 находим: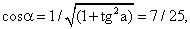
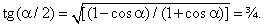Пусть АВ = х. Тогда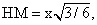 
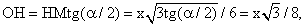
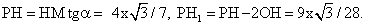Отсюда искомое отношение ОН / О1Н1 = 16/9.Ответ: 16/9.Сфера, вписанная в призмуДиаметр D сферы, вписанной в призму, равен высоте Н призмы: D = 2R = H.Радиус R сферы, вписанной в призму, равен радиусу окружности, вписанной в перпендикулярное сечение призмы.Если в прямую призму вписана сфера, то в основание этой призмы можно вписать окружность.Радиус R сферы, вписанной в прямую призму, равен радиусу окружности, вписанной в основание призмы.Теорема 1Пусть в основание прямой призмы можно вписать окружность, и высота Н призмы равна диаметру D этой окружности. Тогда в эту призму можно вписать сферу диаметром D. Центр этой вписанной сферы совпадает с серединой отрезка, соединяющего центры окружностей, вписанных в основания призмы.Доказательство
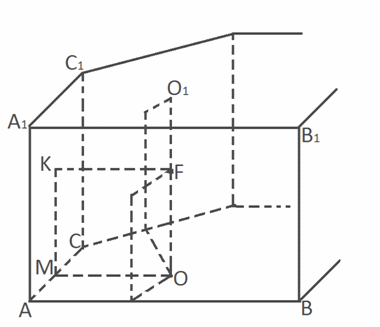Пусть АВС…А1В1С1 … — прямая призма и О — центр окружности, вписанной в ее основание АВС. Тогда точка О равноудалена от всех сторон основания АВС. Пусть О1 — ортогональная проекция точки О на основание А1В1С1. Тогда О1 равноудалена от всех сторон основания А1В1С1, и ОО1 || АА1. Отсюда следует, что прямая ОО1 параллельна каждой плоскости боковой грани призмы, а длина отрезка ОО1 равна высоте призмы и, по условию, диаметру окружности, вписанной в основание призмы. Значит, точки отрезка ОО1 равноудалены от боковых граней призмы, а середина F отрезка ОО1, равноудаленная от плоскостей оснований призмы, будет равноудалена от всех граней призмы. То есть F — центр сферы, вписанной в призму, и диаметр этой сферы равен диаметру окружности, вписанной в основание призмы. Теорема доказана.Теорема 2Пусть в перпендикулярное сечение наклонной призмы можно вписать окружность, и высота призмы равна диаметру этой окружности. Тогда в эту наклонную призму можно вписать сферу. Центр этой сферы делит высоту, проходящую через центр окружности, вписанной в перпендикулярное сечение, пополам.Доказательство
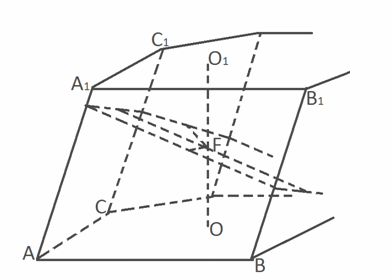Пусть АВС…А1В1С1 … — наклонная призма и F — центр окружности радиусом FK, вписанной в ее перпендикулярное сечение. Поскольку перпендикулярное сечение призмы перпендикулярно каждой плоскости ее боковой грани, то радиусы окружности, вписанной в перпендикулярное сечение, проведенные к сторонам этого сечения, являются перпендикулярами к боковым граням призмы. Следовательно, точка F равноудалена от всех боковых граней.Проведем через точку F прямую ОО1, перпендикулярную плоскости оснований призмы, пересекающую эти основания в точках О и О1. Тогда ОО1 — высота призмы. Поскольку по условию ОО1 = 2FK, то F — середина отрезка ОО1:FK = ОО1 / 2 = FО = FО1, т.е. точка F равноудалена от плоскостей всех без исключения граней призмы. Значит, в данную призму можно вписать сферу, центр которой совпадает с точкой F — центром окружности, вписанной в то перпендикулярное сечение призмы, которое делит высоту призмы, проходящую через точку F, пополам. Теорема доказана.Пример 5.В прямоугольный параллелепипед вписан шар радиуса 1. Найдите объем параллелепипеда.Решение
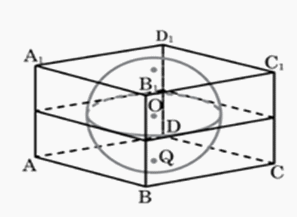Нарисуйте вид сверху. Или сбоку. Или спереди. Вы увидите одно и то же — круг, вписанный в прямоугольник. Очевидно, этот прямоугольник будет квадратом, а параллелепипед будет кубом. Длина, ширина и высота этого куба в два раза больше, чем радиус шара.АВ = 2, а следовательно, объем куба равен 8.Ответ: 8.Пример 6.В правильной треугольной призме со стороной основания, равной 
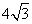, расположены два шара. Первый шар вписан в призму, а второй шар касается одного основания призмы, двух ее боковых граней и первого шара. Найти радиус второго шара.Решение
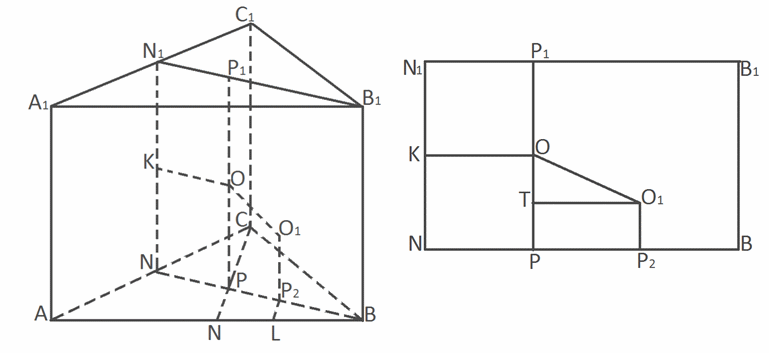Пусть АВСА1В1С1 — правильная призма и точки Р и Р1 — центры ее оснований. Тогда центр шара О, вписанного в эту призму, является серединой отрезка РР1. Рассмотрим плоскость РВВ1. Поскольку призма правильная, то РВ лежит на отрезке BN, который является биссектрисой и высотой ΔАВС. Следовательно, плоскость 
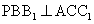и является биссекторной плоскостью двугранного угла при боковом ребре ВВ1. Поэтому любая точка этой плоскости равноудалена от боковых граней АА1ВВ1 и СС1В1В. В частности, перпендикуляр ОК, опущенный из точки О на грань АСС1А1, лежит в плоскости РВВ1 и равен отрезку ОР.Заметим, что KNPO — квадрат, сторона которого равна радиусу шара, вписанного в данную призму.Пусть О1 — центр шара, касающегося вписанного шара с центром О и боковых граней АА1ВВ1 и СС1В1В призмы. Тогда точка О1 лежит плоскости РВВ1, а ее проекция Р2 на плоскость АВС лежит на отрезке РВ.По условию сторона основания равна 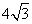, следовательно, PN = 2 и поэтому радиус шара ОР, вписанного в призму, также равен 2. Так как шары с центрами в точках О и О1 касаются друг друга, то отрезок ОО1 = ОР + О1Р2. Обозначим ОР = r, О1Р2 = x. Рассмотрим ΔОО1Т, где 
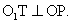В этом треугольнике ОО1 = r + x, OТ = r — x. Поэтому 
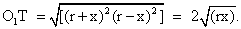Так как фигура О1Р2РТ — прямоугольник, то 
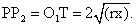Далее, по свойству медиан треугольника РВ = 2r, а Р2В = 2х, поскольку в прямоугольном треугольнике 
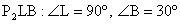и Р2L = х. Поскольку РВ = РР2 + Р2В, то получаем уравнение 
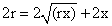, из которого, учитывая неравенство x < r, находим 
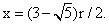Подставив значение r = 2, окончательно находим 
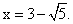Ответ: 
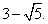Сфера, описанная около многогранника
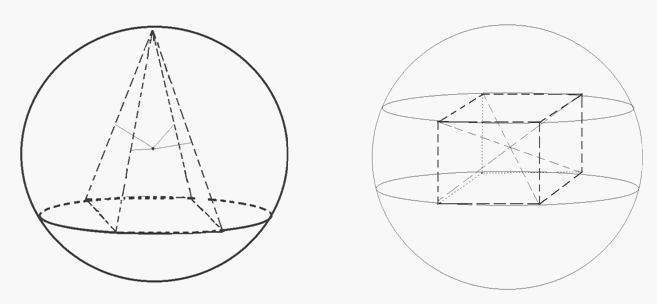Сфера называется описанной около многогранника, если все его вершины лежат на этой сфере. При этом многогранник называется вписанным в сферу.Из определения следует, что если у многогранника существует описанная сфера, то все его грани являются вписанными многоугольниками и, следовательно, не каждый многогранник имеет описанную около него сферу.Например, наклонный параллелепипед не имеет описанной сферы, т.к. вокруг параллелограмма нельзя описать окружность.Центр сферы, описанной около прямой призмы — это середина отрезка, соединяющего центры окружностей, описанных около оснований прямой призмы.Пример 7.Найти радиус описанной около куба сферы, если объем куба 27. Ответ записать в виде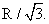 
РешениеОбъем куба 
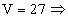ребро куба a = 3. По теореме Пифагора диагональ куба 
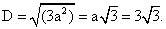Тогда радиус найдем, как половину диагонали куба: 
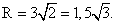Запишем ответ в виде 
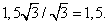Ответ: 1,5.Пример 8.Одно из оснований правильной треугольной призмы принадлежит большому кругу шара радиуса R, а вершины другого основания принадлежат поверхности этого шара. Определить высоту призмы, при которой ее объем будет наибольшим.Решение
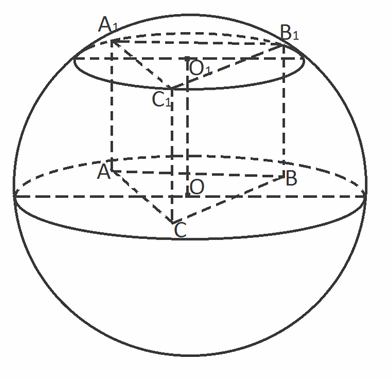Перпендикуляр к плоскости А1В1С1, проведенный из центра описанного около этого треугольника круга, проходит через центр шара. Обозначим ОВ1 = R, ОВ = R1, ВВ1 = h = x.Тогда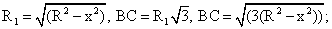 
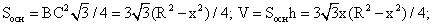
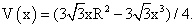Найдем производную, приравняем ее к нулю. Получим:
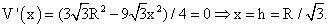Ответ: 
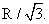Список используемой литературы Видеолекция «Шар и сфера»: 
