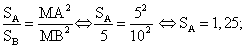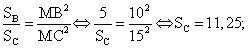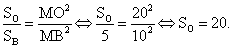Конус
 называется тело, полученное вращением прямоугольного треугольника вокруг оси, содержащей его катет.Конусом
называется тело, полученное вращением прямоугольного треугольника вокруг оси, содержащей его катет.Конусом называется тело, которое состоит из круга — основание конуса
называется тело, которое состоит из круга — основание конуса , точки, не лежащей в плоскости этого круга — вершины конуса
, точки, не лежащей в плоскости этого круга — вершины конуса , и всех отрезков, соединяющих вершину конуса с точками основания.Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса
, и всех отрезков, соединяющих вершину конуса с точками основания.Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса .Полная поверхность конуса
.Полная поверхность конуса состоит из основания и боковой поверхности.Конус называется прямым
состоит из основания и боковой поверхности.Конус называется прямым , если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.Высотой конуса
, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания.Осью прямого конуса
называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания.Осью прямого конуса называется прямая, содержащая его высоту.Сечение конуса плоскостью, проходящей через его ось, называют осевым сечением
называется прямая, содержащая его высоту.Сечение конуса плоскостью, проходящей через его ось, называют осевым сечением .Прямой конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси.Конические сечения
.Прямой конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси.Конические сечения — результат пересечения плоскости с конусом. Возможны 4 основных типа конических сечений: эллипс, парабола, круг, равнобедренный треугольник.
— результат пересечения плоскости с конусом. Возможны 4 основных типа конических сечений: эллипс, парабола, круг, равнобедренный треугольник.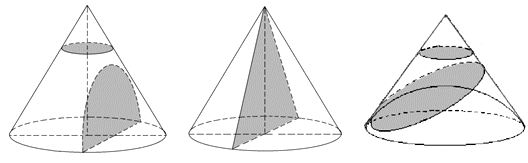 Центр тяжести
Центр тяжести любого конуса лежит на четверти высоты, считая от основания.Плоскость, перпендикулярная оси конуса, отсекает от него меньший конус. Оставшуюся часть называют усеченным конусом
любого конуса лежит на четверти высоты, считая от основания.Плоскость, перпендикулярная оси конуса, отсекает от него меньший конус. Оставшуюся часть называют усеченным конусом . Усеченный конус можно получить и как тело вращения.Усеченным конусом называют тело вращения, образованное вращением прямоугольной трапеции около боковой стороны, перпендикулярной основаниям.Сечениями усеченного конуса
. Усеченный конус можно получить и как тело вращения.Усеченным конусом называют тело вращения, образованное вращением прямоугольной трапеции около боковой стороны, перпендикулярной основаниям.Сечениями усеченного конуса являются: эллипс, парабола, круг, равнобедренная трапеция.Площадь осевого сечения конуса
являются: эллипс, парабола, круг, равнобедренная трапеция.Площадь осевого сечения конуса (равнобедренный треугольник) с радиусом основания R и высотой конуса h: Sосев = Rh.Конус (R — радиус основания, L — образующая, h — высота конуса):
(равнобедренный треугольник) с радиусом основания R и высотой конуса h: Sосев = Rh.Конус (R — радиус основания, L — образующая, h — высота конуса):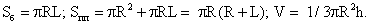 Усеченный конус (R1 и R2 — радиусы оснований; L — образующая, h — высота конуса):
Усеченный конус (R1 и R2 — радиусы оснований; L — образующая, h — высота конуса):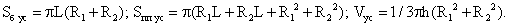 Пример 1.Осевое сечение конуса — правильный треугольник. Определить угол в развертке этого конуса.Решение
Пример 1.Осевое сечение конуса — правильный треугольник. Определить угол в развертке этого конуса.Решение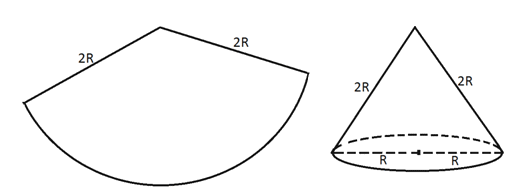 Для конуса длина окружности основания L = 2πR.Для сектора с углом α длина окружности Lα = π(2R)α / 180°.Длина окружности основания конуса равна длине окружности сектора с углом α развертки этого конуса.Т.е. 2πR = π(2R)α / 180°, α = 180°.Ответ: 180°.Пример 2.Угол в развертке конуса равен 90°. Определить угол в осевом сечении этого конуса.Решение
Для конуса длина окружности основания L = 2πR.Для сектора с углом α длина окружности Lα = π(2R)α / 180°.Длина окружности основания конуса равна длине окружности сектора с углом α развертки этого конуса.Т.е. 2πR = π(2R)α / 180°, α = 180°.Ответ: 180°.Пример 2.Угол в развертке конуса равен 90°. Определить угол в осевом сечении этого конуса.Решение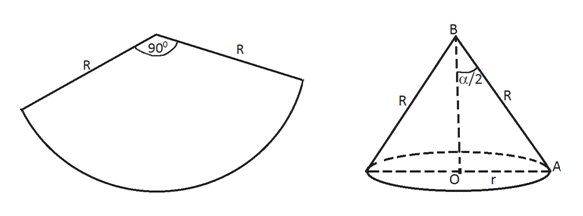 Длина окружности сектора с углом α = 90°:Lα = πRα / 180° = πR90° / 180° = πR/2.Длина окружности основания конуса L = 2πr.Из равенства длин окружностей сектора и основания выразим r — радиус конуса:
Длина окружности сектора с углом α = 90°:Lα = πRα / 180° = πR90° / 180° = πR/2.Длина окружности основания конуса L = 2πr.Из равенства длин окружностей сектора и основания выразим r — радиус конуса: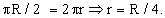 В прямоугольном ∆АОВ: sin(α/2) = r/R = R/4R = ¼, α/2 = arcsin¼, α = 2arcsin¼.Ответ: 2arcsin¼.Пример 3.Радиус основания конуса с вершиной в точке М и центром основания О равен r, а высота конуса равна h. Точка О1 лежит на высоте конуса и МО1 : МО = a : b. Через точку проведено сечение плоскостью, перпендикулярной высоте конуса. Найти площадь полученного сечения и длину отрезка ОО1.Решение
В прямоугольном ∆АОВ: sin(α/2) = r/R = R/4R = ¼, α/2 = arcsin¼, α = 2arcsin¼.Ответ: 2arcsin¼.Пример 3.Радиус основания конуса с вершиной в точке М и центром основания О равен r, а высота конуса равна h. Точка О1 лежит на высоте конуса и МО1 : МО = a : b. Через точку проведено сечение плоскостью, перпендикулярной высоте конуса. Найти площадь полученного сечения и длину отрезка ОО1.Решение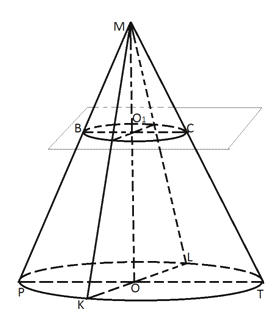 Данное сечение — круг с центром в точке О1 и радиусом равным r1. Рассмотрим осевое сечение конуса, проходящее через концы диаметра РТ основания конуса. Это сечение пересекает круг с центром в точке О1 по отрезку ВС. Поскольку плоскость сечения, проходящая через точку О1, и плоскость основания конуса параллельны, как две плоскости, перпендикулярные одной прямой МО, то ВС || PT. Следовательно, треугольники МВО1 и МРО подобны с коэффициентом подобияk = МВ / МР = ВО1 / РО = МО1 / МО = a / b. Так как по условию РО = r, то из полученной пропорции находим ВО1 = r1 радиус круга, являющегося сечением конуса:
Данное сечение — круг с центром в точке О1 и радиусом равным r1. Рассмотрим осевое сечение конуса, проходящее через концы диаметра РТ основания конуса. Это сечение пересекает круг с центром в точке О1 по отрезку ВС. Поскольку плоскость сечения, проходящая через точку О1, и плоскость основания конуса параллельны, как две плоскости, перпендикулярные одной прямой МО, то ВС || PT. Следовательно, треугольники МВО1 и МРО подобны с коэффициентом подобияk = МВ / МР = ВО1 / РО = МО1 / МО = a / b. Так как по условию РО = r, то из полученной пропорции находим ВО1 = r1 радиус круга, являющегося сечением конуса: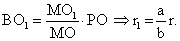 Из той же пропорции следует:
Из той же пропорции следует: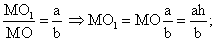
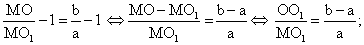
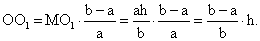 Итак, площадь сечения S1 = πr12 = πr2 ∙ a2 / b2, а длина ОО1 = (b — a)h / b.Ответ: πr2a2 / b2, (b — a)h / b.Разобранный пример №3 позволяет сформулировать теорему.ТеоремаПлощади сечений конуса, параллельных его основанию, относятся, как квадраты их расстояний от вершины конуса.Пример 4.Высота конуса рана 20. Точки А, В, С лежат в указанной последовательности на высоте конуса и делят ее на четыре равные части, причем С — ближайшая к основанию конуса. Площадь сечения, проходящего через точку В, равна 5. Найти площадь основания конуса и площади сечений, проходящих через точки А и С.
Итак, площадь сечения S1 = πr12 = πr2 ∙ a2 / b2, а длина ОО1 = (b — a)h / b.Ответ: πr2a2 / b2, (b — a)h / b.Разобранный пример №3 позволяет сформулировать теорему.ТеоремаПлощади сечений конуса, параллельных его основанию, относятся, как квадраты их расстояний от вершины конуса.Пример 4.Высота конуса рана 20. Точки А, В, С лежат в указанной последовательности на высоте конуса и делят ее на четыре равные части, причем С — ближайшая к основанию конуса. Площадь сечения, проходящего через точку В, равна 5. Найти площадь основания конуса и площади сечений, проходящих через точки А и С.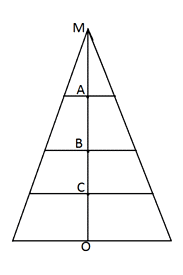 РешениеПоскольку высота конуса МО = 20, а точки А, В, С делят ее на равные части, то МА = 5, МВ = 10, МС = 15. Из теоремы о параллельных сечениях конуса следуют пропорции:Ответ: 20; 1,25; 11,25.Пример 5.Угол при вершине конуса равен β. Какова наибольшая площадь осевого сечения конуса, если величина угла α — угла между образующими, содержащих некоторое сечение конуса, будет меняться?Решение
РешениеПоскольку высота конуса МО = 20, а точки А, В, С делят ее на равные части, то МА = 5, МВ = 10, МС = 15. Из теоремы о параллельных сечениях конуса следуют пропорции:Ответ: 20; 1,25; 11,25.Пример 5.Угол при вершине конуса равен β. Какова наибольшая площадь осевого сечения конуса, если величина угла α — угла между образующими, содержащих некоторое сечение конуса, будет меняться?Решение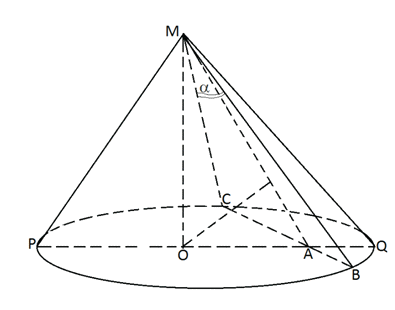 Пусть α — угол между образующими МВ и МС некоторого сечения, содержащего две образующие конуса, т.е.
Пусть α — угол между образующими МВ и МС некоторого сечения, содержащего две образующие конуса, т.е. 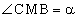 , а угол при вершине конуса, т.е.
, а угол при вершине конуса, т.е. 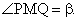 Запишем формулу для площади сечения, как функции от угла α:SMCB = S(α) = ½L2sinα.Заметим, что 0 ≤ α ≤ β.Если β — острый или прямой, то sinα и, значит, S(α) будет монотонно возрастать и поэтому достигнет своего наибольшего значения при α = β. Т.е. в этом случае площадь осевого сечения будет наибольшей.Если β — тупой угол, то наибольшее значение площади сечения будет равно SMCB = S(α) = ½L2, т.к. sinα будет иметь наибольшее значение равное 1, при α = 90°.Дополнительно заметим, что если угол в осевом сечении конуса тупой, то существует такое осевое сечение конуса плоскостью, проходящей через две образующие, площадь которого равна площади осевого сечения.Например, если угол при вершине конуса равен 150°, а образующая 2, то площадь осевого сечения S0 = ½ ∙ 22sin150 = 1. Рассмотрим теперь сечение, содержащее две образующие конуса, угол между которыми равен 30°. Очевидно, что это сечение не осевое. Найдем его площадь: Sсеч = ½ ∙ 22sin30 = 1.Пример 6.В конусе длина образующей вдвое больше его высоты и равна 20. Найти площадь осевого сечения конуса.Решение
Запишем формулу для площади сечения, как функции от угла α:SMCB = S(α) = ½L2sinα.Заметим, что 0 ≤ α ≤ β.Если β — острый или прямой, то sinα и, значит, S(α) будет монотонно возрастать и поэтому достигнет своего наибольшего значения при α = β. Т.е. в этом случае площадь осевого сечения будет наибольшей.Если β — тупой угол, то наибольшее значение площади сечения будет равно SMCB = S(α) = ½L2, т.к. sinα будет иметь наибольшее значение равное 1, при α = 90°.Дополнительно заметим, что если угол в осевом сечении конуса тупой, то существует такое осевое сечение конуса плоскостью, проходящей через две образующие, площадь которого равна площади осевого сечения.Например, если угол при вершине конуса равен 150°, а образующая 2, то площадь осевого сечения S0 = ½ ∙ 22sin150 = 1. Рассмотрим теперь сечение, содержащее две образующие конуса, угол между которыми равен 30°. Очевидно, что это сечение не осевое. Найдем его площадь: Sсеч = ½ ∙ 22sin30 = 1.Пример 6.В конусе длина образующей вдвое больше его высоты и равна 20. Найти площадь осевого сечения конуса.Решение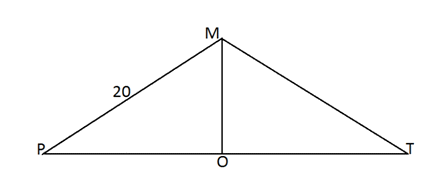 Рассмотрим осевое сечение РМТ конуса. Так как катет МО прямоугольного ∆РМО в два раза меньше гипотенузы РМ, то
Рассмотрим осевое сечение РМТ конуса. Так как катет МО прямоугольного ∆РМО в два раза меньше гипотенузы РМ, то 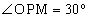 . Следовательно,
. Следовательно, 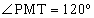 . Теперь площадь осевого сечения можно найти по формуле:
. Теперь площадь осевого сечения можно найти по формуле: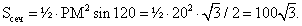 Ответ:
Ответ: 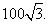 Пример 7.Три образующие конуса попарно перпендикулярны, а длина каждой из них
Пример 7.Три образующие конуса попарно перпендикулярны, а длина каждой из них 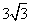 . Найти угол в развертке конуса.Решение
. Найти угол в развертке конуса.Решение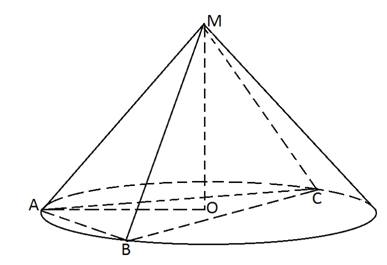 Чтобы найти угол в развертке конуса, нужно знать длину окружности полученного сектора. Эта длина будет равна длине окружности конуса, чтобы узнать которую, надо найти радиус основания конуса r = AO:πRα / 180° = 2πr, α = 360r / R, где R = АМ. (*)Пусть в конусе с вершиной М и центром основания О образующие АМ, ВМ и СМ попарно перпендикулярны. Поэтому треугольники АМВ, ВМС, СМА прямоугольные и равнобедренные, катеты которых соответственно равны. Поэтому эти треугольники равны и, следовательно, равны их гипотенузы, т.е. ∆АВС равносторонний. В ∆АМВ по теореме Пифагора:
Чтобы найти угол в развертке конуса, нужно знать длину окружности полученного сектора. Эта длина будет равна длине окружности конуса, чтобы узнать которую, надо найти радиус основания конуса r = AO:πRα / 180° = 2πr, α = 360r / R, где R = АМ. (*)Пусть в конусе с вершиной М и центром основания О образующие АМ, ВМ и СМ попарно перпендикулярны. Поэтому треугольники АМВ, ВМС, СМА прямоугольные и равнобедренные, катеты которых соответственно равны. Поэтому эти треугольники равны и, следовательно, равны их гипотенузы, т.е. ∆АВС равносторонний. В ∆АМВ по теореме Пифагора: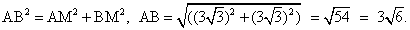 Итак,
Итак, 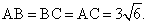 Зная сторону равностороннего ∆АВС, найдем радиус описанной окружности из формулы:
Зная сторону равностороннего ∆АВС, найдем радиус описанной окружности из формулы: 
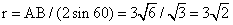 .Подставим в формулу (*):
.Подставим в формулу (*): 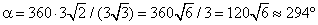 .Ответ: 294.Пример 8.В усеченном конусе радиусы оснований равны r и R (r < R). Определить радиус сечения этого конуса плоскостью, параллельной его основаниям и делящей высоту усеченного конуса в отношении a : b, считая от меньшего основания.Решение
.Ответ: 294.Пример 8.В усеченном конусе радиусы оснований равны r и R (r < R). Определить радиус сечения этого конуса плоскостью, параллельной его основаниям и делящей высоту усеченного конуса в отношении a : b, считая от меньшего основания.Решение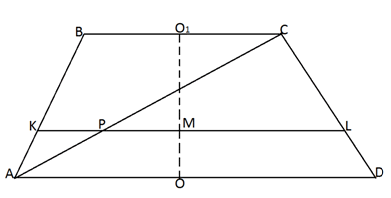 Пусть трапеция АВСD — осевое сечение усеченного и ВС || AD. Тогда ВС = 2r, AD = 2R. Пусть точка М на высоте конуса делит ее так, что О1М : МО = a : b, где О и О1 — центры большего и меньшего оснований конуса соответственно. Проведем через точку М прямую KL || BC. Используя подобие, ∆АКР ~ ∆АВС, найдем:
Пусть трапеция АВСD — осевое сечение усеченного и ВС || AD. Тогда ВС = 2r, AD = 2R. Пусть точка М на высоте конуса делит ее так, что О1М : МО = a : b, где О и О1 — центры большего и меньшего оснований конуса соответственно. Проведем через точку М прямую KL || BC. Используя подобие, ∆АКР ~ ∆АВС, найдем: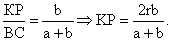 Из подобия ∆АКР ~ ∆АВС, найдем:
Из подобия ∆АКР ~ ∆АВС, найдем: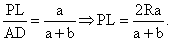 Следовательно,
Следовательно, 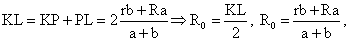 где R0 — радиус сечения.Ответ:
где R0 — радиус сечения.Ответ: 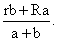 Пример 9.Площади оснований усеченного конуса 4 см2 и 25 см2. Найти площади сечений плоскостями, параллельными его основаниям и делящей высоту на три равные части.Решение
Пример 9.Площади оснований усеченного конуса 4 см2 и 25 см2. Найти площади сечений плоскостями, параллельными его основаниям и делящей высоту на три равные части.Решение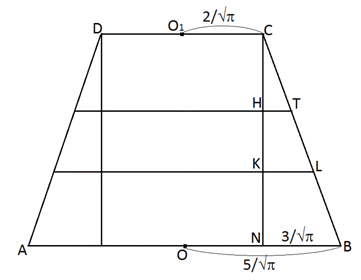 1-й способ:Сечениями конуса являются окружности с радиусами R3 и R4.Найдем радиусы верхнего и нижнего оснований конуса:
1-й способ:Сечениями конуса являются окружности с радиусами R3 и R4.Найдем радиусы верхнего и нижнего оснований конуса: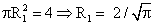
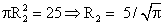
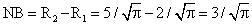 Чтобы найти радиусы R3 и R4 сечений, параллельных основаниям, рассмотрим подобные треугольники:∆NCB ~ ∆KCL ~ ∆HCT с коэффициентом подобия к = 3, следует, что:
Чтобы найти радиусы R3 и R4 сечений, параллельных основаниям, рассмотрим подобные треугольники:∆NCB ~ ∆KCL ~ ∆HCT с коэффициентом подобия к = 3, следует, что: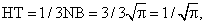 тогда
тогда 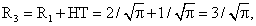
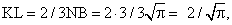 тогда
тогда 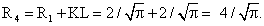 Зная радиусы, найдем площади сечений:
Зная радиусы, найдем площади сечений: 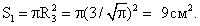
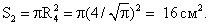 2-й способ:По формуле примера №8 найдем радиус сечения, проходящего через точки К и L:
2-й способ:По формуле примера №8 найдем радиус сечения, проходящего через точки К и L: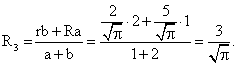 Аналогично найдем радиус сечения, проходящего через точки Н и Т:
Аналогично найдем радиус сечения, проходящего через точки Н и Т: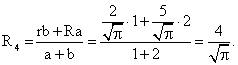 Тогда площади сечений, проходящих через точки К и L и через точки Н и Т соответственно равны:
Тогда площади сечений, проходящих через точки К и L и через точки Н и Т соответственно равны: 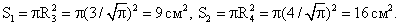 Ответ: 9 см2 и 16 см2.Список используемой литературы Видеолекция «Конус»:
Ответ: 9 см2 и 16 см2.Список используемой литературы Видеолекция «Конус»: