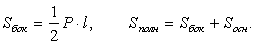Пирамида
 называется многогранник, поверхность которого состоит из многоугольника, называемого основанием пирамиды, и треугольников с общей вершиной, называемых боковыми гранями пирамиды. Пирамида называется n-угольной
называется многогранник, поверхность которого состоит из многоугольника, называемого основанием пирамиды, и треугольников с общей вершиной, называемых боковыми гранями пирамиды. Пирамида называется n-угольной , если ее основанием является n-угольник.
, если ее основанием является n-угольник.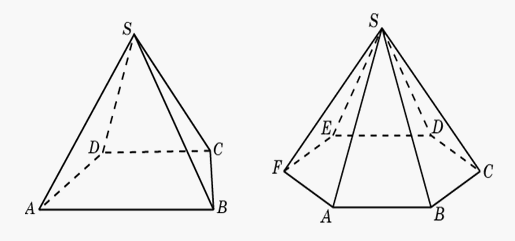 Пирамида называется правильной
Пирамида называется правильной , если её основание — правильный многоугольник и все боковые ребра равны.Пирамида называется прямоугольной
, если её основание — правильный многоугольник и все боковые ребра равны.Пирамида называется прямоугольной , если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.Усечённой пирамидой
, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию. Усечённая пирамида называется правильной, если пирамида, из которой она была получена — правильная.Тетраэдром
называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию. Усечённая пирамида называется правильной, если пирамида, из которой она была получена — правильная.Тетраэдром называется треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды. Кроме того, существует большое различие в понятиях правильная треугольная пирамида и правильный тетраэдр
называется треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды. Кроме того, существует большое различие в понятиях правильная треугольная пирамида и правильный тетраэдр .Элементы пирамиды
.Элементы пирамиды- апофема
 — высота боковой грани правильной пирамиды, проведенная из ее вершины;
— высота боковой грани правильной пирамиды, проведенная из ее вершины; - боковые грани
 — треугольники, сходящиеся в вершине пирамиды;
— треугольники, сходящиеся в вершине пирамиды; - боковые ребра
 — общие стороны боковых граней;
— общие стороны боковых граней; - вершина пирамиды
 — точка, соединяющая боковые рёбра и не лежащая в плоскости основания;
— точка, соединяющая боковые рёбра и не лежащая в плоскости основания; - высота
 — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра);
— отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра); - диагональное сечение пирамиды
 — сечение пирамиды, проходящее через вершину и диагональ основания;
— сечение пирамиды, проходящее через вершину и диагональ основания; - основание
 — многоугольник, которому не принадлежит вершина пирамиды;
— многоугольник, которому не принадлежит вершина пирамиды;
- Если в пирамиде все боковые ребра образуют с плоскостью основания равные углы, то вершина пирамиды проецируется в центр окружности, описанной около основания пирамиды.
- Если в пирамиде длины всех боковых ребер равны, то вершина пирамиды проецируется в центр окружности, описанной около основания пирамиды.
- Если в пирамиде все боковые грани образуют с плоскостью основания равные углы, то вершина пирамиды проецируется в центр окружности, вписанной в основание пирамиды.
- Если в пирамиде длины всех апофем боковых граней равны, то вершина пирамиды проецируется в центр окружности, вписанной в основание пирамиды.
- Боковые ребра правильной пирамиды — равны.
- Боковые грани правильной пирамиды — равные друг другу равнобедренные треугольники.
- Боковые ребра правильной пирамиды образуют с плоскостью основания равные углы.
- Апофемы правильной пирамиды равны.
- Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на высоту боковой грани.
- В правильной усеченной n-угольной пирамиде все боковые ребра равны между собой.
- Все боковые грани правильной усеченной n-угольной пирамиды суть равные равнобедренные трапеции (углы при основаниях равнобедренной трапеции равны).
- В правильной усеченной n-угольной пирамиде все плоские углы при основаниях равны.
- В правильной усеченной n-угольной пирамиде все двугранные углы при основаниях равны.
- В правильной усеченной n-угольной пирамиде все двугранные углы при боковых ребрах равны.
- Центром описанной, около пирамиды, сферы будет точка пересечения плоскостей, проходящих через середины рёбер пирамиды перпендикулярно им. Из этой теоремы следует, что как около любой треугольной, так и около любой правильной пирамиды можно описать сферу.
- В пирамиду можно вписать сферу тогда, когда биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке. Эта точка будет центром сферы.
- Если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна
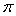 , а каждый из них соответственно
, а каждый из них соответственно 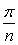 , где n — количество сторон многоугольника основания.
, где n — количество сторон многоугольника основания. - Конус называется вписанным в пирамиду, если вершины их совпадают, а его основание вписано в основание пирамиды. Причём вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой.
- Конус называется описанным около пирамиды, когда их вершины совпадают, а его основание описано около основания пирамиды. Причём описать конус около пирамиды можно только тогда, когда все боковые ребра пирамиды равны между собой.
- Высоты у таких конусов и пирамид равны между собой.
- Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью, вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.
- Цилиндр называется описанным около пирамиды, если вершина пирамиды принадлежит его одному основанию, а другое его основание описано около основания цилиндра. Причём описать цилиндр около пирамиды можно только тогда, когда в основании пирамиды — вписанный многоугольник.
- Свойства тетраэдра
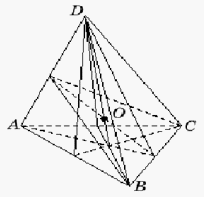
- Биссектральные плоскости двугранных углов тетраэдра пересекаются в одной точке — центре вписанной сферы.
- Плоскости, проходящие через середины ребер тетраэдра и перпендикулярные этим ребрам, пересекаются в одной точке — центре описанной сферы.
- Прямые, перпендикулярные граням тетраэдра, и проходящие через центры их описанных окружностей, пересекаются в одной точке — центре описанной сферы.
- У тетраэдра существует сфера, касающаяся всех его ребер, тогда и только тогда, когда суммы противоположных ребер этого тетраэдра равны.
- Отрезки, соединяющие вершины тетраэдра с точками пересечения медиан противоположных граней, пересекаются в одной точке — центроиде тетраэдра и делятся в этой точке в отношении 3 : 1, считая от вершины.
- Точка пересечения высот правильного тетраэдра делит каждую из его высот в отношении 3:1, считая от вершины, и является центром его вписанной и описанной сфер. При этом, если ребро правильного тетраэдра равно b, то его высота
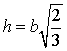 .
. - Теорема (Менелая
 ).
).
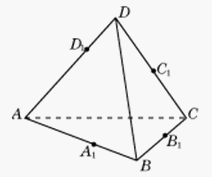 Пусть на ребрах AB, BC, CD и AD тетраэдра ABCD взяты соответственно точки A1, B1, C1 и D1. Для того чтобы эти точки лежали в одной плоскости, необходимо и достаточно, чтобы выполнялось равенство
Пусть на ребрах AB, BC, CD и AD тетраэдра ABCD взяты соответственно точки A1, B1, C1 и D1. Для того чтобы эти точки лежали в одной плоскости, необходимо и достаточно, чтобы выполнялось равенство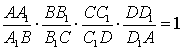 .
. - Теорема (Чевы
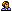 ).
Пусть на ребрах AB, BC, CD и AD тетраэдра ABCD взяты соответственно точки A1, B1, C1 и D1. Плоскости ABC1, BCD1, CDA1 и DAB1 пересекаются в одной точке тогда и только тогда, когда
).
Пусть на ребрах AB, BC, CD и AD тетраэдра ABCD взяты соответственно точки A1, B1, C1 и D1. Плоскости ABC1, BCD1, CDA1 и DAB1 пересекаются в одной точке тогда и только тогда, когда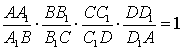 .
. - Бимедианы тетраэдра АС и BD,
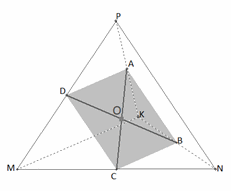 т.е. отрезки, соединяющие середины противоположных ребер тетраэдра, пересекаются в одной точке О — центроиде.
т.е. отрезки, соединяющие середины противоположных ребер тетраэдра, пересекаются в одной точке О — центроиде. - Основанием высоты прямоугольного тетраэдра,
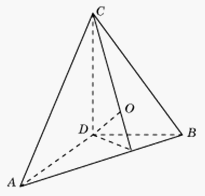 проведенной из вершины с прямыми плоскими углами, является точка пересечения высот противоположной грани.
проведенной из вершины с прямыми плоскими углами, является точка пересечения высот противоположной грани. - Теорема (Пифагора
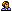 ).
Квадрат площади грани прямоугольного тетраэдра, лежащей против вершины с прямыми плоскими углами, равен сумме квадратов площадей остальных граней этого тетраэдра:SACB2 =SADC2 + SADB2 + SCDB2.
).
Квадрат площади грани прямоугольного тетраэдра, лежащей против вершины с прямыми плоскими углами, равен сумме квадратов площадей остальных граней этого тетраэдра:SACB2 =SADC2 + SADB2 + SCDB2.
- Произвольная пирамида
- Произвольная усечённая пирамида
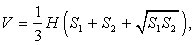 где H — высота, S1 и S2 — площади оснований, V — объем;
где H — высота, S1 и S2 — площади оснований, V — объем; - Правильная усечённая пирамида
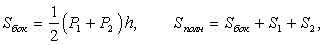 где h — апофема, P1 и P2 — периметры оснований;
где h — апофема, P1 и P2 — периметры оснований; - Правильная пирамида
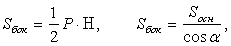 где
где  — двугранный угол при основании;
— двугранный угол при основании;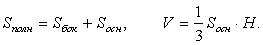
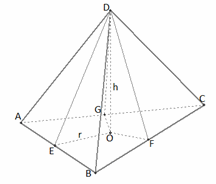 Расстояние от вершины до плоскости основания равно высоте, которая опущена из вершины на основание.Величины апофем пирамиды равны по условию задачи. Высота, опущенная из вершины, является центром вписанной в основание окружности. Таким образом, прямоугольные треугольники, образованные высотой пирамиды и апофемой — равны по двум катетам.Найдем радиус вписанной в основание окружности. Формула радиуса окружности, вписанной в произвольный треугольник: S = pr, где
Расстояние от вершины до плоскости основания равно высоте, которая опущена из вершины на основание.Величины апофем пирамиды равны по условию задачи. Высота, опущенная из вершины, является центром вписанной в основание окружности. Таким образом, прямоугольные треугольники, образованные высотой пирамиды и апофемой — равны по двум катетам.Найдем радиус вписанной в основание окружности. Формула радиуса окружности, вписанной в произвольный треугольник: S = pr, где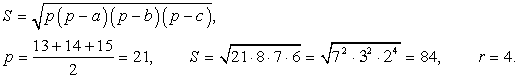 По теореме Пифагора: DE2 = h2 + r2, h2 = 25 - 16 , h2 = 9, h = 3 (см).Ответ: 3.Пример 2.Найдите величину двугранного угла правильного тетраэдра.Решение.
По теореме Пифагора: DE2 = h2 + r2, h2 = 25 - 16 , h2 = 9, h = 3 (см).Ответ: 3.Пример 2.Найдите величину двугранного угла правильного тетраэдра.Решение.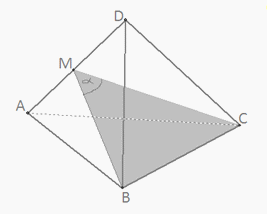 Надо найти угол между двумя пересекающимися медианами двух боковых граней.По теореме Пифагора
Надо найти угол между двумя пересекающимися медианами двух боковых граней.По теореме Пифагора 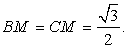 По теореме косинусов:
По теореме косинусов: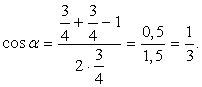 Ответ: arccos(1/3).Пример 3.В основании пирамиды лежит прямоугольный треугольник, один из катетов которого 8 см, а радиус описанной около него окружности равен 5 см. Высота пирамиды равна 12 см. Вычислить боковые ребра пирамиды.Решение.
Ответ: arccos(1/3).Пример 3.В основании пирамиды лежит прямоугольный треугольник, один из катетов которого 8 см, а радиус описанной около него окружности равен 5 см. Высота пирамиды равна 12 см. Вычислить боковые ребра пирамиды.Решение.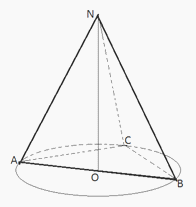 Центр окружности, описанной около прямоугольного треугольника, лежит на его гипотенузе. Кроме того АО = ОС = ОВ = r,поэтому AB = 10 см.
Центр окружности, описанной около прямоугольного треугольника, лежит на его гипотенузе. Кроме того АО = ОС = ОВ = r,поэтому AB = 10 см. ANO =
ANO = DNO =
DNO = CNO по двум катетам, поэтому боковые ребра пирамиды равны. Итак, AN = NB = NC найдем по теореме Пифагора: AN2 = AO2 + ON2 , AN2 = 52 + 122 ,AN =
CNO по двум катетам, поэтому боковые ребра пирамиды равны. Итак, AN = NB = NC найдем по теореме Пифагора: AN2 = AO2 + ON2 , AN2 = 52 + 122 ,AN = 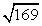 , AN = 13.Ответ: 13, 13, 13.Пример 4.В основании пирамиды лежит равнобедренный треугольник с боковой стороной b и углом при основании
, AN = 13.Ответ: 13, 13, 13.Пример 4.В основании пирамиды лежит равнобедренный треугольник с боковой стороной b и углом при основании  . Все боковые грани образуют с основанием угол
. Все боковые грани образуют с основанием угол  . Найти площадь полной поверхности пирамиды.Решение.
. Найти площадь полной поверхности пирамиды.Решение.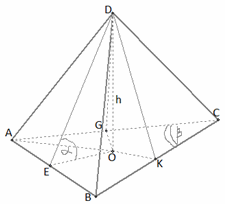 Найдем площадь основания как площадь равнобедренного треугольника, состоящего из двух прямоугольных. В прямоугольном
Найдем площадь основания как площадь равнобедренного треугольника, состоящего из двух прямоугольных. В прямоугольном  AKС:AK = AС sin
AKС:AK = AС sin = b sin
= b sin СK = AС cos
СK = AС cos = b cos
= b cos SABK = AK·СK/2 = b2sin
SABK = AK·СK/2 = b2sin cos
cos / 2, откудаSABC = 2SABK = b2sin
/ 2, откудаSABC = 2SABK = b2sin cos
cos = 0,5b2sin 2
= 0,5b2sin 2 (по формуле двойного угла).Площадь боковой поверхности пирамиды:Sб =SADC + SADB + SBDC = 2SADC + SBDC.Высота пирамиды проецируется в точку О основания, которая одновременно является центром вписанной окружности с радиусом ОЕ = r. Радиус вписанной окружности найдем как r = S/p.Учитывая, что BC = 2СK, то BC = 2bcos
(по формуле двойного угла).Площадь боковой поверхности пирамиды:Sб =SADC + SADB + SBDC = 2SADC + SBDC.Высота пирамиды проецируется в точку О основания, которая одновременно является центром вписанной окружности с радиусом ОЕ = r. Радиус вписанной окружности найдем как r = S/p.Учитывая, что BC = 2СK, то BC = 2bcos , найдем полупериметр основания:p = (b + b + 2bcos
, найдем полупериметр основания:p = (b + b + 2bcos ) / 2, p = (2b + 2bcos
) / 2, p = (2b + 2bcos ) / 2, p = 2b(1 + cos
) / 2, p = 2b(1 + cos ) / 2, p = b(1 + cos
) / 2, p = b(1 + cos ).Радиус вписанной окружности: r = S / p,r = 0,5b2sin2
).Радиус вписанной окружности: r = S / p,r = 0,5b2sin2 / b(1 + cos
/ b(1 + cos ) = 0,5b sin2
) = 0,5b sin2 / (1 + cos
/ (1 + cos ).Апофемы пирамиды равны:DG = DK = DE = r/cos
).Апофемы пирамиды равны:DG = DK = DE = r/cos = 0,5b sin2
= 0,5b sin2 / (1 + cos
/ (1 + cos )cos
)cos SADB = AB·DE/2 = 0,25b2sin2
SADB = AB·DE/2 = 0,25b2sin2 /(1 + cos
/(1 + cos )cos
)cos .SBDC =BC·DK/2 = 2bcos
.SBDC =BC·DK/2 = 2bcos ·0,5bsin2
·0,5bsin2 /2(1 + cos
/2(1 + cos )cos
)cos = 0,5b2cos
= 0,5b2cos sin2
sin2 /(1 + cos
/(1 + cos )cos
)cos Sб = 2·0,25b2sin2
Sб = 2·0,25b2sin2 /(1 + cos
/(1 + cos )cos
)cos + 0,5b2cos
+ 0,5b2cos sin2
sin2 /(1 + cos
/(1 + cos )cos
)cos Sб = 0,5b2sin2
Sб = 0,5b2sin2 (1 +cos
(1 +cos ) / (1 + cos
) / (1 + cos )cos
)cos Sб = 0,5b2sin2
Sб = 0,5b2sin2 / cos
/ cos Sп = SABC + Sб = 0,5b2sin2
Sп = SABC + Sб = 0,5b2sin2 + 0,5b2sin2
+ 0,5b2sin2 / cos
/ cos Sп = 0,5b2sin 2
Sп = 0,5b2sin 2 [1 + 1/cos
[1 + 1/cos ]Ответ: 0,5b2sin 2
]Ответ: 0,5b2sin 2 [1 + 1/cos
[1 + 1/cos ].Пример 5.Сторона основания правильной четырехугольной пирамиды равна b. Двугранные углы при основании равны
].Пример 5.Сторона основания правильной четырехугольной пирамиды равна b. Двугранные углы при основании равны  . Найти площадь полной поверхности пирамиды.Решение.
. Найти площадь полной поверхности пирамиды.Решение.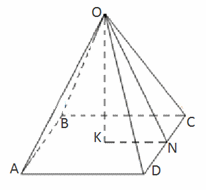 Поскольку пирамида правильная, то ее высота проецируется в центр основания.Значит KN = b/2.
Поскольку пирамида правильная, то ее высота проецируется в центр основания.Значит KN = b/2. OKN — прямоугольный: ON = KN/cos
OKN — прямоугольный: ON = KN/cos  = b/2cos
= b/2cos  Площадь
Площадь  DOC: SDOC = DC·ON/2,SDOC = (b·b/2cos
DOC: SDOC = DC·ON/2,SDOC = (b·b/2cos  )/2 = b2 /4cos
)/2 = b2 /4cos  .Площадь боковой поверхности правильной пирамиды будет равна площади всех ее боковых граней:Sб = 4b2/4cos
.Площадь боковой поверхности правильной пирамиды будет равна площади всех ее боковых граней:Sб = 4b2/4cos  = b2/cos
= b2/cos  .Площадь полной поверхности пирамиды : Sп = b2/cos
.Площадь полной поверхности пирамиды : Sп = b2/cos  + b2 = b2 (1 + 1/cos
+ b2 = b2 (1 + 1/cos ).Ответ: b2(1 + 1/cos
).Ответ: b2(1 + 1/cos ).Пример 6.В правильной четырёхугольной пирамиде сторона основания равна b, высота равна 3b. Найдите углы наклона боковых рёбер и боковых граней к плоскости основания.Решение.
).Пример 6.В правильной четырёхугольной пирамиде сторона основания равна b, высота равна 3b. Найдите углы наклона боковых рёбер и боковых граней к плоскости основания.Решение.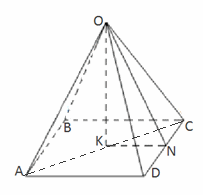 Обозначим углы наклона боковых граней к плоскости основания
Обозначим углы наклона боковых граней к плоскости основания 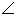 ONK =
ONK =  , а углы наклона боковых ребер к плоскости основания
, а углы наклона боковых ребер к плоскости основания 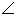 OСK =
OСK =  .
. OKN - прямоугольный, OK= 3b, KN = b/2, tg
OKN - прямоугольный, OK= 3b, KN = b/2, tg  = OK/KN = 3b/(b/2) = 6,
= OK/KN = 3b/(b/2) = 6,  = arctg 6Диагональ квадрата со стороной b равна
= arctg 6Диагональ квадрата со стороной b равна 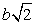 .
. OKC — прямоугольный: (обозначим
OKC — прямоугольный: (обозначим 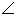 KCO =
KCO = )
)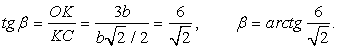 Ответ: угол наклона граней arctg 6; угол наклона ребер
Ответ: угол наклона граней arctg 6; угол наклона ребер 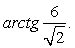 Пример 7.Найти величину двугранного угла при основании правильной четырехугольной пирамиды, если её боковые ребра наклонены к плоскости основания под углом
Пример 7.Найти величину двугранного угла при основании правильной четырехугольной пирамиды, если её боковые ребра наклонены к плоскости основания под углом 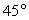 .Решение.
.Решение.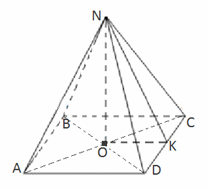 Обозначим искомый угол
Обозначим искомый угол 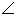 NKO =
NKO = .Поскольку боковые ребра правильной четырехугольной пирамиды наклонены к основанию под углом
.Поскольку боковые ребра правильной четырехугольной пирамиды наклонены к основанию под углом 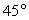 , то в
, то в  ANC
ANC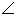 ANC =
ANC =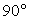 . Т.е.
. Т.е.  ANC - прямоугольный, причем
ANC - прямоугольный, причем  NOC =
NOC =  ANO — прямоугольные и равнобедренные, NO = OC.Пусть длина ребра пирамиды равна b, тогда, исходя из того, что треугольник ANC — прямоугольный равнобедренный,AC2 = NC2 + AN2 = 2b2, AC = b
ANO — прямоугольные и равнобедренные, NO = OC.Пусть длина ребра пирамиды равна b, тогда, исходя из того, что треугольник ANC — прямоугольный равнобедренный,AC2 = NC2 + AN2 = 2b2, AC = b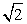 , откуда OC = AC/2 = b
, откуда OC = AC/2 = b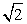 /2 = b/
/2 = b/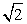 = NO.В прямоугольном
= NO.В прямоугольном  COD: CD2 = OC2 + OD2 = 2OC2 = 2(b/
COD: CD2 = OC2 + OD2 = 2OC2 = 2(b/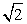 )2 = b2, CD = b, тогдаKC = CD/2 = b/2,OK2 = OC2 - KC2 = (b/
)2 = b2, CD = b, тогдаKC = CD/2 = b/2,OK2 = OC2 - KC2 = (b/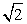 )2 – (b/2)2, OK = b/2.В прямоугольном
)2 – (b/2)2, OK = b/2.В прямоугольном  KON: tg
KON: tg = NO/OK = b/
= NO/OK = b/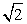 : b/2 =
: b/2 = 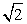 . Откуда
. Откуда  = arctg
= arctg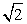 Ответ: arctg
Ответ: arctg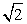 .Пример 8.Боковая грань правильной треугольной пирамиды представляет собой правильный треугольник, площадь которого 16
.Пример 8.Боковая грань правильной треугольной пирамиды представляет собой правильный треугольник, площадь которого 16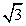 см2. Вычислить периметр основания пирамиды.Решение.
см2. Вычислить периметр основания пирамиды.Решение.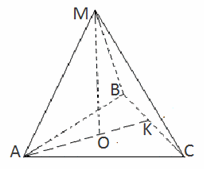 Так как основание правильной пирамиды и боковые грани являются равносторонними треугольниками, то все боковые грани равны и все ребра пирамиды одинаковые. Площадь боковой грани найдем как площадь равностороннего треугольника:
Так как основание правильной пирамиды и боковые грани являются равносторонними треугольниками, то все боковые грани равны и все ребра пирамиды одинаковые. Площадь боковой грани найдем как площадь равностороннего треугольника: 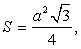
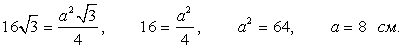 Тогда периметр основания пирамиды равен 8·3 = 24 см.Ответ: 24.Пример 9.В правильной треугольной пирамиде высота равна 10 см, а сторона основания 16 см. Найти площадь боковой поверхности.Решение.
Тогда периметр основания пирамиды равен 8·3 = 24 см.Ответ: 24.Пример 9.В правильной треугольной пирамиде высота равна 10 см, а сторона основания 16 см. Найти площадь боковой поверхности.Решение. Основанием треугольной пирамиды является равносторонний треугольник, поэтому AO является радиусом описанной около основания окружности, ОК — радиусом вписанной окружности, которые найдем из формул:
Основанием треугольной пирамиды является равносторонний треугольник, поэтому AO является радиусом описанной около основания окружности, ОК — радиусом вписанной окружности, которые найдем из формул: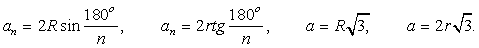 Тогда R = АО = 16/
Тогда R = АО = 16/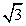 , r = ОК = 8/
, r = ОК = 8/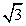 ,АК = КС sin60 = 4
,АК = КС sin60 = 4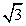 .Sосн = BC·AK/2 = 16·4
.Sосн = BC·AK/2 = 16·4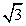 /2 = 32
/2 = 32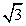 — площадь основания
— площадь основания МОК: МК2 = МО2 + ОК2 = 100 + (8/
МОК: МК2 = МО2 + ОК2 = 100 + (8/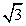 )2 = 364/3,
)2 = 364/3, 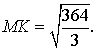
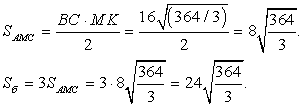 Ответ:
Ответ: 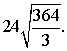 Пример 10.Сторона правильной треугольной пирамиды равна 3 см а угол между боковой гранью и основанием пирамиды равен
Пример 10.Сторона правильной треугольной пирамиды равна 3 см а угол между боковой гранью и основанием пирамиды равен 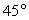 . Найдите площадь полной поверхности пирамиды.Решение.
. Найдите площадь полной поверхности пирамиды.Решение. Поскольку пирамида правильная, в ее основании лежит равносторонний треугольник. Поэтому площадь основания равна
Поскольку пирамида правильная, в ее основании лежит равносторонний треугольник. Поэтому площадь основания равна 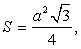
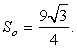 Для того, чтобы найти площадь боковой грани, вычислим апофему KM:
Для того, чтобы найти площадь боковой грани, вычислим апофему KM: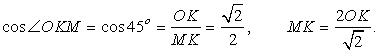 OК — это радиус вписанной окружности,
OК — это радиус вписанной окружности, 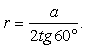
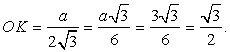 Тогда
Тогда 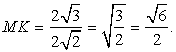
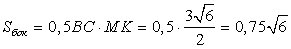 Откуда площадь полной поверхности будет равна
Откуда площадь полной поверхности будет равна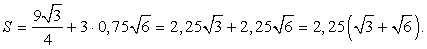 Ответ:
Ответ: 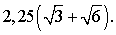 Пример 11.Высота правильной треугольной пирамиды 4 см, а ее апофемы 8 см. Вычислить площадь боковой поверхности пирамиды.Решение.
Пример 11.Высота правильной треугольной пирамиды 4 см, а ее апофемы 8 см. Вычислить площадь боковой поверхности пирамиды.Решение. Исходя из того, что MK = 8, MO = 4, sin
Исходя из того, что MK = 8, MO = 4, sin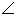 OKM = MO/MK = 1/2откуда
OKM = MO/MK = 1/2откуда 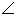 OKM = arcsin1/2 =
OKM = arcsin1/2 =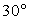 . Тогда cos30 = KO / MK,
. Тогда cos30 = KO / MK, 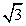 /2 = KO/ 8,KO = 8
/2 = KO/ 8,KO = 8 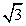 /2 = 4
/2 = 4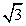 KO — это радиус вписанной окружности в основание правильной треугольной пирамиды.
KO — это радиус вписанной окружности в основание правильной треугольной пирамиды.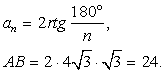 Площадь боковой грани найдем, как площадь равнобедренного треугольника:Sб = 1/2 · 24 · 8 = 96 см2.Откуда площадь боковой поверхности пирамидыS = 3·Sб = 3 · 96 = 288 см2.Ответ: 288 см2.Пример 12.Найдите площадь поверхности треугольной пирамиды, у которой каждое ребро
Площадь боковой грани найдем, как площадь равнобедренного треугольника:Sб = 1/2 · 24 · 8 = 96 см2.Откуда площадь боковой поверхности пирамидыS = 3·Sб = 3 · 96 = 288 см2.Ответ: 288 см2.Пример 12.Найдите площадь поверхности треугольной пирамиды, у которой каждое ребро 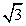 .Решение.Поскольку все ребра треугольной пирамиды равны - она является правильной. Площадь поверхности правильной треугольной пирамиды равна S = a2
.Решение.Поскольку все ребра треугольной пирамиды равны - она является правильной. Площадь поверхности правильной треугольной пирамиды равна S = a2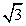 .Тогда S = 3
.Тогда S = 3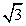 .Ответ: 3
.Ответ: 3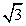 .Пример 13.Основание пирамиды — правильный треугольник со стороной
.Пример 13.Основание пирамиды — правильный треугольник со стороной 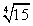 см.Одно из боковых ребер пирамиды перпендикулярно к основанию, а два других наклонено к плоскости основания под углом
см.Одно из боковых ребер пирамиды перпендикулярно к основанию, а два других наклонено к плоскости основания под углом 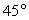 . Найти площадь боковой грани.Решение.
. Найти площадь боковой грани.Решение.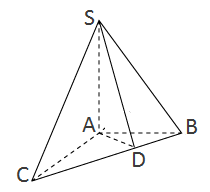 По условию
По условию  ABC — равносторонний. SA — перпендикуляр к плоскости ABC, AB =
ABC — равносторонний. SA — перпендикуляр к плоскости ABC, AB = 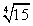 . Так как SA — перпендикулярно плоскости
. Так как SA — перпендикулярно плоскости  ABC, то AB — проекция SB, AC — проекция SC. Отсюда
ABC, то AB — проекция SB, AC — проекция SC. Отсюда 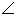 SBA =
SBA = 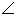 SCA =
SCA = 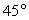 .Проведем медиану AD(она же и высота) в
.Проведем медиану AD(она же и высота) в  ABC. Соединим точки S и D. По теореме о трех перпендикулярах
ABC. Соединим точки S и D. По теореме о трех перпендикулярах  (гипотенуза
(гипотенуза  ASD больше катета).Так как,
ASD больше катета).Так как, 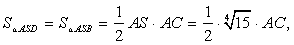 а
а 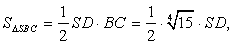 то наибольшую площадь имеет грань SBC.Из
то наибольшую площадь имеет грань SBC.Из  ASc имеем:
ASc имеем: 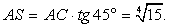 .Из
.Из  ADC имеем:
ADC имеем:  .Из
.Из  ASD имеем:
ASD имеем: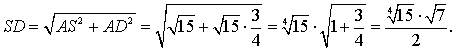 Тогда площадь:
Тогда площадь: 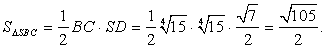 Ответ:
Ответ: 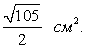 Пример 14.В правильной треугольной пирамиде сторона основания равна 2 см, а высота пирамиды 4 см. Найти угол наклона боковых ребер к плоскости основания.Решение.
Пример 14.В правильной треугольной пирамиде сторона основания равна 2 см, а высота пирамиды 4 см. Найти угол наклона боковых ребер к плоскости основания.Решение.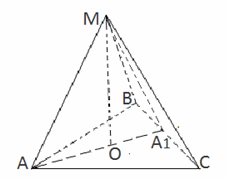 Рассмотрим правильную треугольную пирамиду ABCM с основанием ABC, AB = BC = AC = 2 см, высотой MO = 4 смИскомым углом является
Рассмотрим правильную треугольную пирамиду ABCM с основанием ABC, AB = BC = AC = 2 см, высотой MO = 4 смИскомым углом является  MAA1.Вычислим длину AA1.
MAA1.Вычислим длину AA1.  ABC — равносторонний со стороной AC = 2 см. Так как A1C = 1 см, то есть возможность применить теорему Пифагора для
ABC — равносторонний со стороной AC = 2 см. Так как A1C = 1 см, то есть возможность применить теорему Пифагора для  A1CA, в котором
A1CA, в котором  A1 =
A1 = 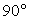 :
: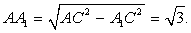 Воспользуемся далее свойством медиан произвольного треугольника: медианы треугольника пересекаются и точкой пересечения делятся в отношении 1:2. Поэтому
Воспользуемся далее свойством медиан произвольного треугольника: медианы треугольника пересекаются и точкой пересечения делятся в отношении 1:2. Поэтому 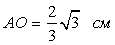 .Обратим внимание, что для нахождения
.Обратим внимание, что для нахождения 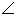 MAA1 нужно рассмотреть
MAA1 нужно рассмотреть  АОМ, в котором катет MO = 4 см (по условию задачи), второй катет
АОМ, в котором катет MO = 4 см (по условию задачи), второй катет 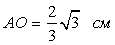 (по вычислению). Так как нам известны длины двух катетов в прямоугольном треугольнике АОМ, то для нахождения искомого угла обратимся к тангенсу острого угла прямоугольного треугольника.
(по вычислению). Так как нам известны длины двух катетов в прямоугольном треугольнике АОМ, то для нахождения искомого угла обратимся к тангенсу острого угла прямоугольного треугольника.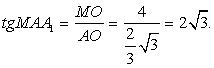 Ответ:
Ответ: 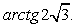 Список используемой литературы Видеолекция «Пирамида»:
Список используемой литературы Видеолекция «Пирамида»: 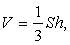 где
где 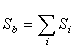 ;
;