Векторы на плоскости и в пространстве
— это направленный отрезок. Его длиной считают длину отрезка.Если даны две точки M1 (x1, y1, z1) и M2 (x2, y2, z2), то вектор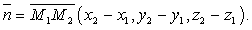
Расстояние между двумя точками — это длина отрезка М1М2 или длина вектора n:
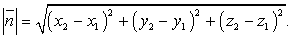Если даны два вектора 
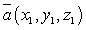и 
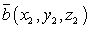, то:- Длины векторов:
- Сумма векторов:
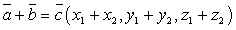Суммой двух векторов a и b является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма); или вектор, соединяющий начало первого вектора с концом последнего — по правилу треугольника.Суммой трех векторов a, b, c называется диагональ параллелепипеда, построенного на этих векторах(правило параллелепипеда). - Разность векторов:
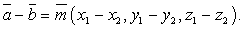
- Умножение вектора на число (скаляр):
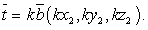Векторы t и b называются коллинеарными, т.е. лежат на параллельных прямых или на одной прямой. Пропорциональные координаты — условие коллинеарности векторов. - Скалярное произведение векторов:
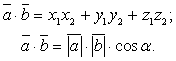Если скалярное произведение равно нулю, то векторы перпендикулярны. - Угол между векторами a и b, точнее его косинус:
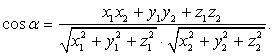
- Векторное произведение векторов:
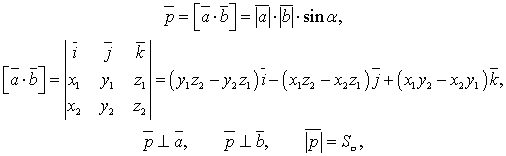где S — площадь параллелограмма, построенного на векторах a, b.Если 
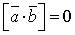, то данные векторы коллинеарные (параллельны прямой).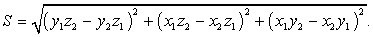
- Смешанное произведение векторов
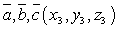
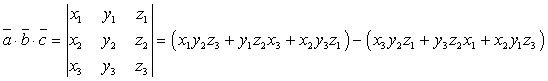Если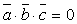 
, то данные векторы компланарные (принадлежат плоскости или параллельны ей).Три ненулевых вектора a, b, cкомпланарны, когда один из них выражается через два других, т.е.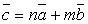 
, где n, m — числа.Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку, т.е. 
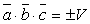. - Введение системы координат.Как лучше ввести систему координат для самых часто встречающихся в задаче C2 многогранников, рассмотрим на примерах.Координаты вершин куба
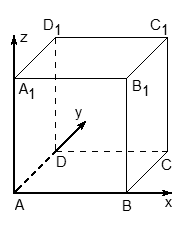
- Начало координат — в точке A;
- Сторона куба — единичный отрезок.
- Ось ОХ направляем по ребру AB, ОY — по ребру AD, а ось OZ — по ребру AA1.Для нижней плоскости куба:
Для верхней плоскости куба:Точка
A
B
C
D
Координаты
(0; 0; 0)
(1; 0; 0)
(1; 1; 0)
(0; 1; 0)
Точка
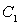
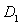
Координаты
(0; 0; 1)
(1; 0; 1)
(1; 1; 1)
(0; 1; 1)
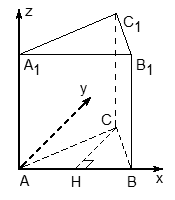
- Начало координат — в точке A;
- Сторона призмы — единичный отрезок, если иное не указано в условии задачи;
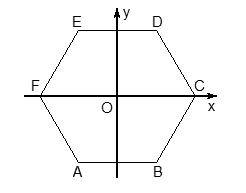
- Ось OX направляем по ребру AB, OZ — по ребру AA1, а ось OY расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC.Заметим, что ось Y НЕ совпадает с ребром AC, т.к. треугольник ABC — равносторонний, в нем все углы по 60°. А углы между осями координат должны быть по 90°, поэтому сверху картинка будет выглядеть так:
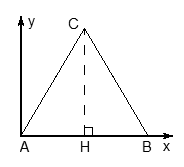Проведем в этом треугольнике высоту CH. Треугольник ACH — прямоугольный, причем AC = 1, поэтомуAH = 1 · cos A = cos 60°; CH = 1 · sin A = sin 60°. Эти факты нужны для вычисления координат точки C.Получаем следующие координаты точек:
A
B
C
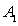
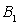
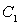
(0;0;0)
(1;0;0)
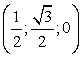
(0;0;1)
(1;0;1)
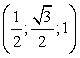
Заметим, что начало координат НЕ совпадает с вершиной многогранника! Это позволяет значительно уменьшить объем вычислений.OZ перпендикулярна плоскости OXY: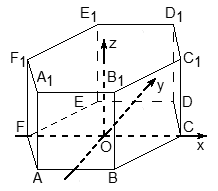
Пусть все ребра нашей правильной шестигранной призмы равны 1.Координаты нижнего основания:
Координаты верхнего основания:A
B
C
D
E
F
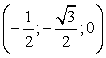
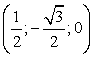
(1;0;0)
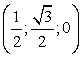
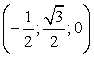
(-1;0;0)
Координаты вершин четырехугольной пирамидыРазберем только самый простой случай — правильную четырехугольную пирамиду, все ребра которой равны. 
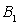
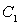
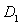
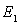
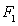
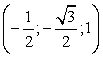
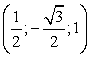
(1;0;1)
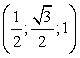
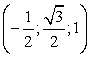
(-1;0;1)
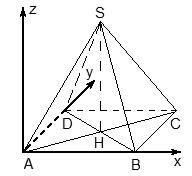Начало координат в точке A, единичный отрезок AB = 1, ось OX направим вдоль AB, ось OY — вдоль AD, а ось OZ — вверх, перпендикулярно плоскости OXY.Чтобы найти координаты вершин, проведем высоту SH. Рассмотрим плоскость OXY: в основании лежит квадрат, его координаты известны. Найдем координаты точки S. Поскольку SH — высота к плоскости OXY, точки S и H отличаются лишь координатой z. Длина отрезка SH — это и есть координата z для точки S, поскольку H = (0,5; 0,5; 0).Треугольники ABC и ASC равны по трем сторонам (AS = CS = AB = CB = 1, а сторона AC — общая). Следовательно, SH = BH. Но BH — половина диагонали квадрата ABCD, т.е. BH = AB · sin 45°. Получаем координаты всех точек:
Мы рассмотрели лишь самые распространенные многогранники, однако этих примеров достаточно, чтобы самостоятельно вычислить координаты любых других фигур. Поэтому можно приступать, собственно, к методам решения конкретных задач.Пример 1.В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; - 1; 7) и C = (- 4; 3; - 2). Найти координаты векторов AB, AC и BC.Решение.Рассмотрим вектор AB: его начало находится в точке A, а конец — в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A: AB = (3 - 1; - 1 - 6; 7 - 3) = (2; - 7; 4).Аналогично, начало вектора AC — все та же точка A, зато конец — точка C. Поэтому имеем: AC = (- 4 - 1; 3 - 6; - 2 - 3) = (- 5; - 3; - 5).Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B: BC = (- 4 - 3; 3 - (- 1); - 2 - 7) = (- 7; 4; - 9).Ответ: AB(2; - 7; 4); AC(- 5; - 3; - 5); BС (- 7; 4; - 9).Пример 2.Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).Решение.Поскольку координаты векторов даны, подставляем их в формулу №6:A
B
C
D
S
(0;0;0)
(1;0;0)
(1;1;0)
(0;1;0)
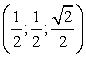
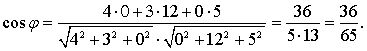Ответ: 36/65.Пример 3.Вычислить площадь треугольника с вершинами А(1;-1;2), В (5;-6;2), С(1;3;-1).Решение.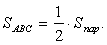
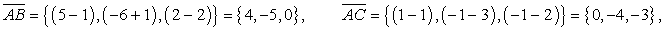тогда площадь треугольника АВС будет вычисляться следующим образом:
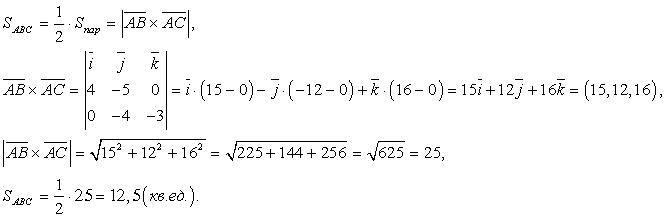Ответ: 12,5.Пример 4.Вычислить смешанное произведение векторов 
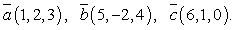Решение.
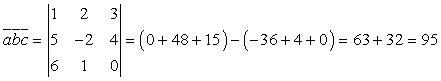Ответ: 95. - Вычисление направляющих векторов прямыхНаправляющим вектором прямой называется вектор параллельный данной прямой.Прямая задается парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим, так называемый, направляющий вектор прямой: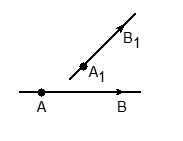
Угол между двумя прямыми — это угол между их направляющими векторами.Пример 5.В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, проведены прямые AB1 и AC1. Найдите координаты направляющих векторов этих прямых.Решение.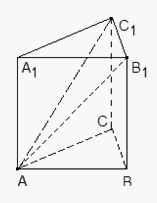
Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA1, ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.A(0; 0; 0), B1(1; 0; 1), тогда AB1 (1 - 0; 0 - 0; 1 - 0) = AB1(1; 0; 1) — направляющий вектор прямой AB1 .
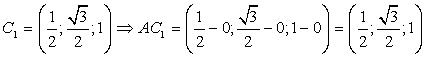— направляющий вектор для прямой AC1.
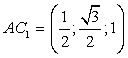Ответ: AB1 = (1; 0; 1). - Вычисление нормалей плоскостейУравнение плоскости в трехмерном пространстве: Ax + By + Cz + D = 0, где A, B, C и D — действительные числа, причем, если плоскость проходит через начало координат, то D = 0. А если не проходит, то D = 1.Нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.Вектор, перпендикулярный к плоскости Ax + By + Cz + D = 0, имеет координаты: n = (A; B; C).В задачах типа С2 часто требуется найти угол между прямой и плоскостью. Этот угол легко найти формуле №6 как синус угла между нормалью и направляющим вектором прямой. (Синус, т.к.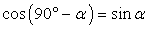
).Пример 6.Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.Решение.Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат —точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:A · 2 + B · 0 + C · 1 + 1 = 0 
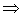2A + C + 1 = 0.Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:A · 0 + B · 1 + C · 1 + 1 = 0 B + C + 1 = 0;A · 2 + B · 1 + C · 0 + 1 = 02A + B + 1 = 0.Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:
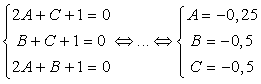Получили, что уравнение плоскости имеет вид: - 0,25A - 0,5B - 0,5C + 1 = 0.Ответ: - 0,25A - 0,5B - 0,5C + 1 = 0Пример 7.Плоскость задана уравнением 7x - 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.Решение.Используя третью формулу, получаем n = (7; - 2; 4).Ответ: (7; - 2; 4).Пример 8.В кубе ABCDA1B1C1D1 проведено сечение A1BC1. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA1 соответственно.Решение.
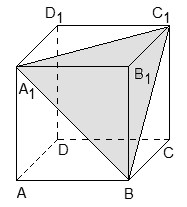Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A1, B и C1, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.Подставим вместо x, y и z координаты точки A1 = (0; 0; 1). Имеем:A · 0 + B · 0 + C · 1 + 1 = 0 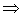C + 1 = 0 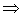C = - 1.Аналогично, для точек B = (1; 0; 0) и C1 = (1; 1; 1) получим уравнения:A · 1 + B · 0 + C · 0 + 1 = 0 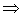A + 1 = 0 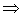A = - 1;A · 1 + B · 1 + C · 1 + 1 = 0 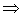A + B + C + 1 = 0.Но коэффициенты A = - 1 и C = - 1 нам уже известны, поэтому остается найти коэффициент B:B = - 1 - A - B = - 1 + 1 + 1 = 1.Получаем уравнение плоскости: - х + у - z + 1 = 0. Следовательно, координаты нормального вектора равны n(- 1; 1; - 1).Ответ: (- 1; 1; - 1)Пример 9.В кубе ABCDA1B1C1D1 проведено сечение AA1C1C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA1 соответственно.Решение.
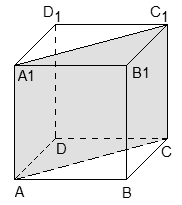В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0.Поскольку плоскость проходит через точки A1 и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство. Подставим вместо x, y и z координаты точки A1(0; 0; 1): A · 0 + B · 0 + C · 1 = 0 C = 0.Аналогично, для точки C (1; 1; 0): A · 1 + B · 1 + C · 0 = 0 A + B = 0 A = - B.Положим B = 1. Тогда A = - B = - 1, и уравнение всей плоскости имеет вид: - A + B = 0. Следовательно, координаты нормального вектора равны n (- 1; 1; 0).Ответ: (- 1; 1; 0). - Координаты середины отрезкаПусть отрезок задан своими концами — точками A = (xa; ya; za) и B = (xb; yb; zb). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:
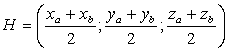Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.Пример 10.Единичный куб ABCDA1B1C1D1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA1 соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A1B1. Найдите координаты этой точки.Решение.
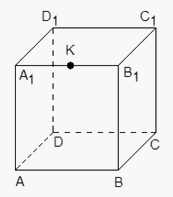Поскольку точка K — середина отрезка A1B1, ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A1 = (0; 0; 1) и B1 = (1; 0; 1). Теперь найдем координаты точки K:
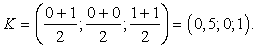Ответ: (0,5; 0; 1).Пример 11.Единичный куб ABCDA1B1C1D1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA1 соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A1B1C1D1.Решение.
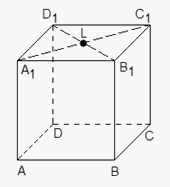Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A1L = C1L, т.е. точка L — это середина отрезка A1C1. Но A1 (0; 0; 1), C1 (1; 1; 1), поэтому имеем:
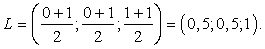Ответ: (0,5; 0,5; 1). - Вычисление расстояния от точки до плоскостиДана точка М(x0 ,y0 ,z0 ) и уравнение плоскости: Ax + By + Cz + D = 0, где A, B, C и D — действительные числа. Напомним, что если плоскость проходит через начало координат, то D = 0, а если не проходит, то D = 1. Тогда d — расстояние от данной точки до плоскости вычисляют по формуле:
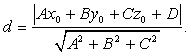Пример 12.В примере 8 найти расстояние от точки D до плоскости А1С1В.Решение.В примере 8 мы нашли уравнение плоскости: - x + y - z + 1 = 0. Подставим координаты точки D(0; 1; 0) и значения нормального вектора n(-1; 1; -1) в формулу:
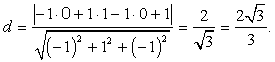Ответ: 
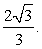Пример 13.В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите расстояние от точки A до плоскости BCA1.Решение.
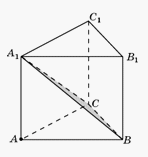Подставим в уравнение плоскости Ax + By + Cz + D = 0 координаты точек А1(0; 0; 1), В(1; 0; 0), С(1/2;
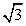/2; 0). Найдем уравнение плоскости из системы уравнений:
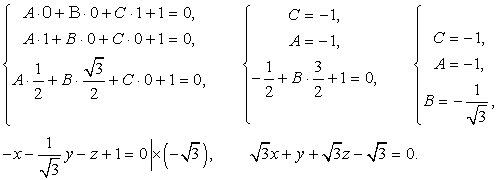Тогда расстояние между точкой М и плоскостью:
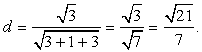Ответ: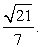 
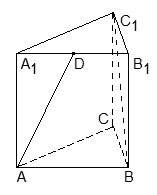Очевидно, речь идет о косинусе угла между двумя прямыми. Введем систему координат: начало координат поместим в точку A, единичный отрезок равен AB = 1. Ось x направим вдоль AB, ось z — вдоль AA1, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью ABC.Найдем координаты вектора AD: A(0; 0; 0), точка D — середина отрезка A1B1, причем A1 (0; 0; 1), B1 (1; 0; 1), тогда D (0,5; 0; 1) — координаты середины отрезка равны среднему арифметическому координат концов.Итак, находим координаты вектора AD:AD = (0,5 - 0; 0 - 0; 1 - 1) = (0,5; 0; 1) 
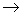(1; 0; 2) — избавились от дробей, умножив координаты вектора на 2.Теперь найдем координаты вектора BC1: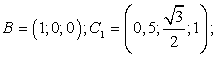 
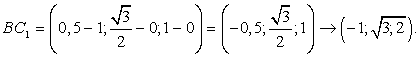Координаты вектора BC1 также оптимизировали, умножив все на 2.
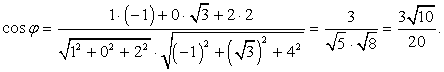Ответ: 
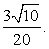Пример 15.В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E и F — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BF.Решение.
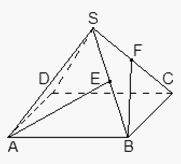Введем систему координат следующим образом: начало координат — точка A, единичный отрезок равен AB = 1. Ось x направим вдоль AB, ось y — вдоль AD, а ось z направим вверх, т.е. перпендикулярно плоскости ABC. Найдем координаты векторов AE и BF.Координаты точек A(0; 0; 0) и B(1; 0; 0) находятся легко. Точки E и F — середины отрезков SB и SC соответственно, поэтому для нахождения их координат нам потребуются точки C и S:
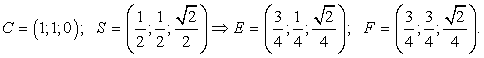Координаты точек E и F нашли, проведя диагональ основания, высоту и воспользовались теоремой Пифагора.Найдем и оптимизируем координаты векторов AE и BF:
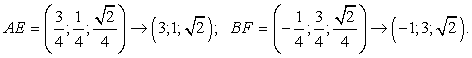В обоих случаях координаты вектора умножены на 4, чтобы избавиться от дробей. Осталось найти косинус:
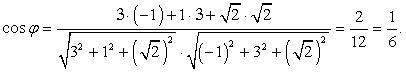Ответ: 1/6.Пример 16.В кубе ABCDA1B1C1D1 отмечены точки E и F — середины ребер A1B1 и B1C1 соответственно. Найдите угол между прямыми AE и BF.Решение.
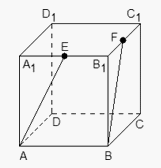Введем систему координат: начало в точке A, оси x, y, z направим вдоль AB, AD и AA1 соответственно. Единичный отрезок равен AB = 1.Найдем координаты направляющих векторов для прямых.Найдем координаты вектора AE: A (0; 0; 0), Е (0,5; 0; 1). Поскольку точка E — середина отрезка A1B1, ее координаты равны среднему арифметическому координат концов. Заметим, что начало вектора AE совпадает с началом координат, поэтому AE (0,5; 0; 1).Найдем координаты вектора BF. B(1; 0; 0), F (1; 0,5; 1), F — середина отрезка B1C1. Имеем: BF(1 - 1; 0,5 - 0; 1 - 0) = BF (0; 0,5; 1).Итак, косинус угла между прямыми — это косинус угла между направляющими векторами, поэтому имеем:
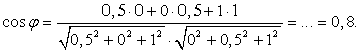Ответ: arccos 0,8.Пример 17.В правильной трехгранной призме ABCA1B1C1, все ребра которой равны 1, отмечены точки D и E — середины ребер A1B1 и B1C1соответственно. Найдите угол между прямыми AD и BE.Решение.
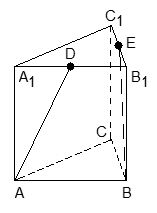Введем систему координат: начало координат в точке A, ось x направим вдоль AB, z — вдоль AA1. Ось y направим так, чтобы плоскость OXY совпадала с плоскостью ABC. Единичный отрезок равен AB = 1.Найдем координаты направляющих векторов для искомых прямых.Для начала найдем координаты вектора AD. Рассмотрим точки: A (0; 0; 0), D (0,5; 0; 1), D — середина отрезка A1B1. Поскольку начало вектора AD совпадает с началом координат, получаем AD = (0,5; 0; 1).Теперь найдем координаты вектора BE. B (1; 0; 0), точка E — середина отрезка C1B1:
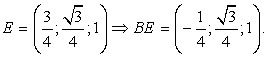Осталось найти косинус угла:
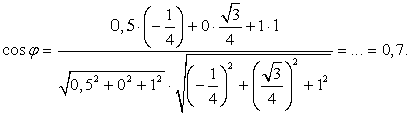Ответ: arccos 0,7.Пример 18.В правильной шестигранной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, отмечены точки K и L — середины ребер A1B1 и B1C1 соответственно. Найти угол между прямыми AK и BL.Решение.
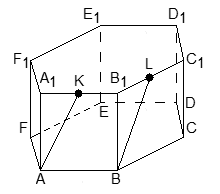Введем систему координат: начало координат поместим в центр нижнего основания, ось x направим вдоль FC, ось y — через середины отрезков AB и DE, а ось z — вертикально вверх. Единичный отрезок равен AB = 1. Выпишем координаты интересующих нас точек:
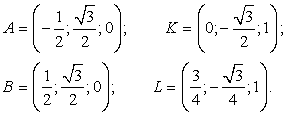Точки K и L — середины отрезков A1B1 и B1C1 соответственно, поэтому их координаты находятся через среднее арифметическое. Зная точки, найдем координаты направляющих векторов AK и BL:
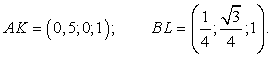Теперь найдем косинус угла:
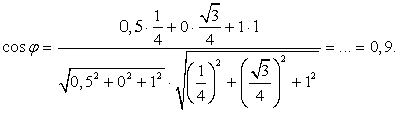Ответ: arccos 0,9.Список используемой литературы Видеолекция «Векторы на плоскости и в пространстве»: 
