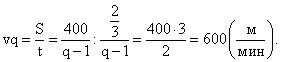Комбинированные задачи
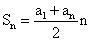Сумма первых n членов 2-я формула 
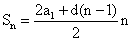Характеристическое свойство 
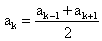Свойство крайних членов a1 + an = a2 + an-1 = a3 + an-2 = …Основные формулы геометрической прогрессииРекуррентная формула n-го члена: bn+1 = bn qФормула n-го члена: bn = b1 qn-1Сумма первых n членов 1-я формула 
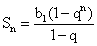Сумма первых n членов 2-я формула 
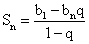Сумма бесконечной геометрической прогрессии 
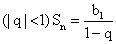Характеристическое свойство 
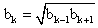Пример 1.Известно, что 1-й, 7-й и 25 члены арифметической прогрессии с ненулевой разностью составляют геометрическую прогрессию. Найти q.РешениеРассмотрим геометрическую прогрессию, члены которой: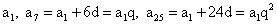
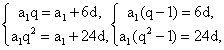Если разделим второе уравнение на первое, то получим q + 1 = 4, q = 3.Ответ: 3.Пример 2.Три различных числа a, b, c образуют в указанном порядке геометрическую прогрессию. Числа: a + b, b + c, a + c образуют в указанном порядке арифметическую прогрессию. Найти знаменатель геометрической прогрессии.Дано:Г.П.: a1, a1q, a1q2.А.П.: a1 + a1q, a1q + a1q2, a1 + a1q2.Найти q.РешениеВоспользуемся характеристическим свойством арифметической прогрессии: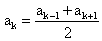 
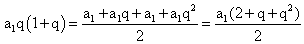
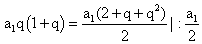2q + 2q2 — 2 — q — q2 = 0q2 + q — 2 = 0, q = -2, q = 1.Знаменатель геометрической прогрессии не может равняться 1.Ответ: -2.Пример 3.Первый член возрастающей арифметической прогрессии равен 0,2. Найти разность прогрессии, если известно, что при делении каждого ее члена на номер этого члена получается геометрическая прогрессия и число членов прогрессии больше трех.Дано:Г.П.: (0,2 + d)/2; (0,2 + 2d)/3; (0,2 + 3d)/4.Найти d.РешениеВоспользуемся характеристическим свойством геометрической прогрессии: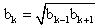 
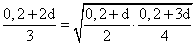. Возведем обе части в квадрат:1/9(0,22 + 4 · 0,2d + 4d2) = 1/8(0,22 + 0,2d + 0,6d + 3d2)| · 728(0,04 + 0,8d + 4d2) = 9 (0,04 + 0,8d + 3d2)0,32 + 6,4d + 32d2 = 0,36 + 7,2d + 27d25d2 — 0,8d — 0,04 = 0, d = 0,2, d = -0,04.По условию арифметическая прогрессия возрастающая, поэтому разность d > 0.Ответ: 0,2.Пример 4.Три отличных от нуля числа образуют арифметическую прогрессию, а квадраты этих чисел образуют геометрическую прогрессию. Найти все возможные знаменатели последней прогрессии.Дано:А.П.: 
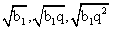Г.П.: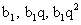 
Найти q.РешениеВоспользуемся характеристическим свойством арифметической прогрессии: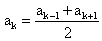 
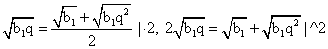
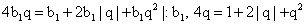
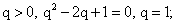
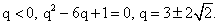Ответ: 
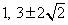.Пример 5.Цифры трехзначного числа составляют геометрическую прогрессию. Если из данного числа вычесть 297, то получится число, написанное теми же цифрами, но в обратном порядке. Если же к цифрам данного числа, начиная с разряда сотен, прибавлять соответственно 8,5 и 1, то полученные суммы составят арифметическую прогрессию. Найти исходное число.РешениеПусть исходное число 
.
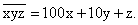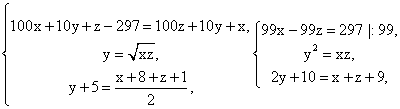
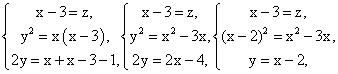Решим второе уравнение: х2 — 4х + 4 = х2 — 3х, х = 4, тогда у = х — 2 = 2, z = x — 3 = 1.Ответ: 421.Пример 6.Найти четыре числа, из которых первые три составляют геометрическую прогрессию, а последние три составляют арифметическую прогрессию, причем сумма крайних чисел равна 32, а сумма средних чисел равна 24.РешениеПусть x, y, z, t — данные числа.
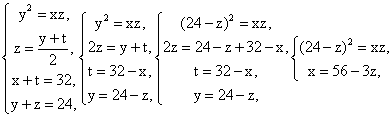(24 — z)2 = (56 — 3z)z; 576 — 48z + z2 = 56z — 3z2, 4z2 — 104z + 576 = 0,z = 18 или z = 8x = 56 — 3z = 2 или x = 32y = 24 — z = 6 или y = 16t = 32 — x = 30 или t = 0.Ответ: 2, 6, 18, 30 или 32, 16, 8, 0.Пример 7.Сумма первых десяти членов арифметической прогрессии равна 155, а сумма первых двух членов геометрической прогрессии равна 9. Найти эти прогрессии, если первый член арифметической прогрессии равен знаменателю геометрической прогрессии, а первый член геометрической прогрессии равен разности арифметической прогрессии.РешениеЕсли подставим данные задачи в формулы суммы и n-го члена арифметической прогрессии, то получим систему уравнений: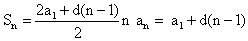
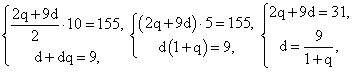Подставим второе уравнение системы в первое и решим его:
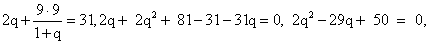q = 2 или q = 12,5. Тогда d = 3 или d = 2/3.Ответ: 2; 5; 8; … и 3; 6; 12; … или 25/2; 79/6; 83/6; … и 2/3; 25/3; 625/6; …Пример 8.При каком значении параметра a значения функции y = x3 — 6x2 + 9x + a в точке х = 2 и в точках экстремума, взятые в некотором порядке, образуют геометрическую прогрессию?РешениеФункция определена на всей числовой прямой. Достаточно легко найти точки экстремума данной функции:y' = 3x2 — 12x + 9 = 3(x2 — 4x + 3) = 3(x — 1 )(x — 3)y' = 0 при х = 1, х = 3.Найдем значение функции в точках экстремума и в точке х = 2:у(3) = a; у(2) = 2 + a; у(1) = 4 + a.Так как порядок чисел не определен, то необходимо проверить характеристическое свойство геометрической прогрессии, все комбинации:- 1) проверим порядок: a; 2 + a; 4 + a: (2 + a)2 = a(4 + a); 4 + 4a + a2 = 4a + a2;4 = 0, неверно;2) проверим порядок: a; 4 + a; 2 + a: (4 + a)2 = a(2 + a); 16 + 8a + a2 = 2a + a2;6a = -16; a = -8/3;3) проверим порядок: 4 + a; a; 2 + a: a2 = (4 + a)(2 + a); a2 = 8 + 6a + a2;6a = -8; a = -4/3.
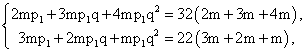Разделим все уравнения на m > 0.56-030.gifЧтобы избавиться от третьего слагаемого, содержащего вторую степень, умножим второе уравнение на (-4 ) и сложим его с первым уравнением: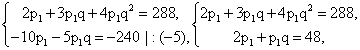
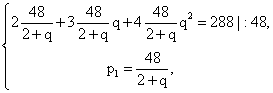Решим первое уравнение:
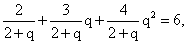2 + 3q + 4q2 = 12 + 6q, 4q2 — 3q — 10 = 0, q = -1,25 или q = 2. Отрицательный корень не удовлетворяет условию задачи.Итак, р1 = 48/(2 + 2) = 12%, р2 = p1q = 12 · 2 = 24%, p3 = р1q2 = 12 · 22 = 48%.Ответ: 12, 24, 48.Пример 10.Три конькобежца, скорости которых в некотором порядке образуют геометрическую прогрессию, одновременно стартуют (из одного места) по кругу. Через некоторое время второй конькобежец обгоняет первого, пробежав на 400 м больше его. Третий конькобежец пробегает то расстояние, которое пробежал первый к моменту обгона его вторым, за время на 2/3 минуты больше, чем первый. Найти скорость первого конькобежца.РешениеНетрудно догадаться, что самый «быстрый» из конькобежцев — это второй, на втором месте — первый, и самый «медленный» — третий. Поэтому пусть скорости конькобежцев в возрастающем порядке:v3 = v, v1 = vq, v2 = vq2.
|
S |
v |
t |
I |
S |
vq |
t |
I I |
S + 400 |
vq2 |
t |
I I I |
S |
v |
t + 2 / 3 |
- Используя первые две строки таблицы, найдем S из системы:
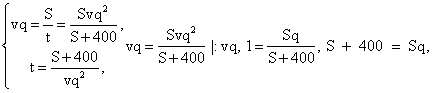S(q — 1) = 400, S = 400 / (q - 1). - Используя первую и третью строки таблицы, найдем t из системы:
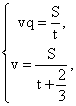Разделим первое уравнение на второе, получим: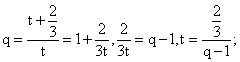
- Найдем скорость первого конькобежца:
