Комбинированные задачи
Задачи, рассмотренные в данном разделе, обобщают сведения комбинаторики, статистики и теории вероятностей.Основные формулы комбинаторики

 

Порядок важен

Порядок неважен

Без повторений

С повторениями

 

Размещения

Перестановки

Сочетания

Правило умноженияПусть объекты А и В не зависят друг от друга. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами.Правило суммыЕсли некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то:
    1) выбрать либо А, либо В можно (m + n) способами, если А и В не имеют общих элементов.2) выбрать либо А, либо В можно (m + n — d) способами, если А и В имеют d общих элементов.
Другими словами, при объединении взаимоисключающих действий (событий, вариантов) число их комбинаций складывается.Вероятностью наступления события А называют число, равное отношению числа событий, в которых это событие А произошло (благоприятствующих А), к общему числу равновозможных событий: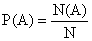Операции с вероятностями
  1. Если события А и Внесовместны, то вероятность наступления или А, или В, или А и В вместе равна Р (А + В) = Р(А) + Р(В).Если А и В — любые события, а АВ — событие, включающее исходы и А, и В, то вероятность наступления или А, или В равна Р(А + В) = Р(А) + Р(В) — Р(АВ).
  2. Если А и В — взаимно противоположные события, то Р(А) + Р(В) = 1
  3. Если события А и В независимы, то Р(АВ) = Р(А) ∙ Р(В).
Пример 1.Какова вероятность выпасть «четырем» или «шести» очкам при одном бросании кости?РешениеТак как кость правильная, то любое число очков от 1 до 6 выпадет с вероятностью 1/6 (одна из шести граней кубика). Одновременно и 4, и 6 выпасть не могут, т.к. у нас лишь один бросок. Значит, мы имеем дело с непересекающимися исходами, поэтому 1/6 + 1/6 = 1/3Ответ: 1/3Пример 2.Из 6 учебников только 3 в переплете. Наудачу взяли 2 учебника. 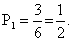Какова вероятность, что они оба в переплете?РешениеИспользуя формулу для вероятности, получим, что вероятность того, что первый учебник в переплете Когда первый учебник в переплете взяли, то осталось 5 учебников, из которых 2 в переплете, т.е. вероятность вытащить второй учебник в переплете 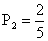. Тогда вероятность, что оба учебника в переплете 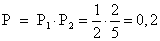Ответ: 0,2.Пример 3.Класс, в котором учится 12 девочек и 12 мальчиков, случайным образом делят на две равные группы для занятий на компьютерах. Какова вероятность того, что мальчиков и девочек в них окажется поровну?РешениеПереформулируем задачу: из 24 учеников этого класса случайно отбирают 12. Какова вероятность, что среди них ровно 6 мальчиков? (Убедитесь, что это действительно та же задача!) Всего способов выбора 12 человек из 24 будет: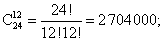причем все эти способы равновозможные. Благоприятные исходы: среди выбранных 12 человек находится ровно 6 мальчиков. Как сформировать любой такой исход? Сначала нужно выбрать любые 6 из 12 мальчиков, а потом добавить к ним любые 6 из 12 девочек. Общее количество таких вариантов выбора можно найти по правилу умножения: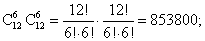Искомая вероятность будет равна: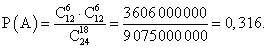Ответ: 0,316Пример 4.В группе пять человек: Ваня, Саша, Маша, Таня и Коля. По жребию двое из них выбраны дежурными. Найти вероятность того, что это Ваня и Таня.РешениеЧисло элементарных событий в этом опыте равно числу сочетаний из 5 по 2: 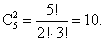Все элементарные события равновозможные. Событию А «дежурят Ваня и Таня» благоприятствует только одно элементарное событие. Поэтому 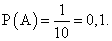Ответ: 0,1.Пример 5.В ящике 4 красных и 2 желтых флажка. Из него наудачу извлекают 3 флажка. Какова вероятность того, что все эти флажки красные?РешениеЧисло элементарных событий в этом опыте равно 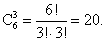Все они равновероятны. Число благоприятных событий для события А «вынули три красных флажка» равно числу способов выбрать 3 красных флажка из 4 красных флажков, имеющихся в ящике. Это число равно 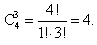Поэтому 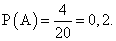Ответ: 0,2.Пример 6.Найти вероятность того, что, извлекая наудачу 5 флажков из ящика, в котором 8 красных и 7 синих флажков, мы вытащим ровно 3 красных и 2 синих флажка.РешениеОбщее число элементарных событий равно числу сочетаний из 15 флажков по 5: 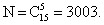Набрать 3 красных флажка из 8 можно одним из 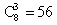способов. Точно так же, набрать 2 синих флажка из 7 можно одним из 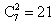способов. Следовательно, число исходов, благоприятствующих событию А «3 красных и 2 синих», равно 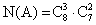. Итак: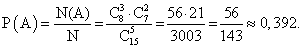Ответ: 0,392.Пример 7.Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.РешениеОбозначим через В событие — набраны две нужные цифры. Всего можно набрать столько различных цифр, сколько может быть составлено размещений из десяти цифр по две, т. е. A102 = 10 ∙ 9 = 90. Таким образом, общее число возможных элементарных исходов равно 90. Эти исходы несовместны, равновозможные и образуют полную группу. Благоприятствует событию В лишь один исход. Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов: Р(В) = 1/90.Ответ: 1/90.Пример 8.Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 4.РешениеОбщее число равновозможных исходов испытания равно 6 ∙ 6 = 36 (каждое число выпавших очков на одной кости может сочетаться со всеми числами очков другой кости). Среди этих исходов благоприятствуют событию А только 3 исхода: (1; 3), (3; 1), (2; 2) (в скобках указаны числа выпавших очков). Следовательно, искомая вероятность Р (A) = 3 / 36 = 1 / 12.Ответ: 1/12.Пример 9.В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди 6 взятых наудачу деталей 4 стандартных.РешениеОбщее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т.е. числу сочетаний из 10 элементов по 6 элементов (С106).Определим число исходов, благоприятствующих интересующему нас событию А (среди шести взятых деталей 4 стандартных). Четыре стандартные детали можно взять из семи стандартных деталей C74 способами; при этом остальные 6 — 4 = 2 детали должны быть нестандартными; взять же 2 нестандартные детали из 10 — 7 = 3 нестандартных деталей можно С32 способами. Следовательно, число благоприятствующих исходов равно C74 ∙ C32.Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов: P(A) = (C74 ∙ C32) / C106 = 1/2.Ответ: 1/2.Пример 10.Из колоды в 36 карт одну за другой вытягивают две карты. Какова вероятность того, что они одного цвета, если первую вытащенную карту назад не возвращаем (выбор без возвращения)?Решение1-й способПодсчитаем общее количество исходов по правилу умножения: для первой карты у нас 36 возможных исходов, для второй — 35 вариантов (одну уже вытянули). Отсюда общее количество исходов n = 36 ∙ 35 = 1260.Событие «карты одного цвета» означает или «карты красного цвета» или «карты черного цвета».Теперь подсчитаем исходы, при которых обе карты красного цвета: для первой карты — 18 вариантов, для второй карты (если мы хотим, чтобы она была того же цвета, что и первая) — 17 вариантов (18-ю карту взяли первой). Отсюда количество благоприятных для нашего события исходов будет m1 = 18 ∙ 17 = 306. Такое же число исходов будет для карт черного цвета, т.е. m2 = 306. Тогда по правилу сложения общее число благоприятных исходов:m = m1 + m2 = 306 + 306 = 612, а искомая вероятность: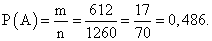Ответ: 0,486.2-й способПорядок важен. Найдем вероятность, используя формулу размещения: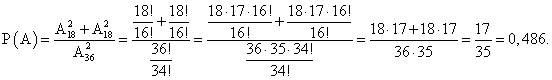Ответ: 0,486.Пример 11.Из колоды в 36 карт одну за другой вытягивают две карты. Какова вероятность того, что они одного цвета, если первую вытащенную карту возвращаем обратно в колоду (выбор с возвращением)?РешениеОтличие от примера 6 только в том, что можно повторно вытянуть ту же самую карту. Поэтому общее количество исходов будет n = 36 ∙ 36 = 1296, а количество благоприятных событий, т.е., что карты одного цвета: m = m1 + m2 = 18 ∙ 18 + 18 ∙ 18 = 648.Осталось найти вероятность, что карты окажутся одного цвета: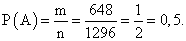Ответ: 0,5Пример 12.На книжной полке случайным образом расставляют 6 учебников. Какова вероятность, что учебник математики и учебник литературы окажутся рядом?РешениеОбщее количество всех возможных вариантов расположения шести книг на полке легко подсчитать с помощью правила умножения: на первое место можно поставить любую из 6 книг, на второе — любую из 5 оставшихся и т.д. Всего получаем 6 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 6! = 720 исходов.Поставить на полку учебник математики можно шестью различными способами, после чего поставить рядом с ним учебник литературы можно одним или двумя различными способами. Это зависит от того, куда мы поставили учебник математики — на крайнее место или нет. Для этого разобьем все множество благоприятных исходов на два класса:Заметим, что эти классы действительно не пересекаются и исчерпывают все множество благоприятных исходов — ведь, в конце концов, учебник математики стоит либо на краю, либо где-то в середине.Посчитаем число исходов в 1-м классе: место с краю для учебника математики можно выбрать двумя способами, после чего учебник литературы можно поставить рядом с ним только одним способом, после чего оставшиеся 4 места можно занять 4! способами. Значит, в этом классе будет 2 ∙ 1 ∙ 4! = 48 исходов.Посчитаем число исходов во 2-ом классе: место в середине для учебника математики можно выбрать четырьмя способами, после чего учебник литературы можно поставить рядом с ним двумя способами, после чего оставшиеся 4 места можно занять 4! способами. Значит, в этом классе будет 4 ∙ 2 ∙ 4! = 192 исхода.Итого 48 + 192 = 240 благоприятных исходов. 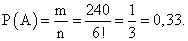Вероятность интересующего нас события будет:Ответ: 0,33.Пример 13.Вы получаете 6 карт из колоды. Какова вероятность, что среди них есть хотя бы один туз?РешениеОбозначим событие, о котором идет речь в задаче, через А и найдем вероятность противоположного события В = {среди шести вынутых карт нет ни одного туза}.Число всех равновозможных исходов данного эксперимента будет n = 36 ∙ 35 ∙ 34 ∙ 33 ∙ 32 ∙ 31, а число исходов, благоприятных для события В: n = 32 ∙ 31 ∙ 30 ∙ 29 ∙ 28 ∙ 27.Отсюда 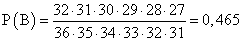, а значит P(A) = 1 — 0,465 = 0,535.Ответ: 0,535.Прогнозирование частотыКакую практическую пользу можно извлечь из подсчета вероятностей?Вы знаете, что с ростом числа экспериментов частота стремится к вероятности. Значит, по известной вероятности можно прогнозировать частоту повторения интересующего нас события в будущем. При этом вероятность может быть найдена любым из известных нам способов (в том числе оценена по уже имеющейся частоте).Пример 14.При проведении контроля качества среди 1000 случайно отобранных деталей оказалось 5 бракованных. Сколько бракованных деталей следует ожидать среди 25 000 деталей?РешениеПо результатам контроля можно оценить вероятность события А = {произведенная деталь бракованная}. Приближенно она будет равна его частоте: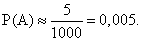Следует ожидать такую частоту и в будущем, поэтому среди 25 000 деталей окажется около 25 000 ∙ 0,005 = 125 бракованных.Пример 15.Население города Калуги составляет около 400 000 жителей. Сколько калужан родились 29 февраля?Решение29 февраля бывает только в високосном году — один раз в четыре года, следовательно, для случайно выбранного человека его день рождения попадает на 29 февраля с вероятностью: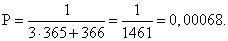Это значит, что среди 400 000 жителей Калуги следует ожидать около 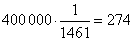человек, которым приходится праздновать свой день рождения раз в четыре года.На прогнозировании частоты основан один интересный способ определения численности популяций, используемый в биологии.Пример 16.Из озера выловили 86 рыб, которых пометили и отпустили обратно в озеро. Через неделю произвели повторный отлов — на этот раз поймали 78 рыб, среди которых оказалось 6 помеченных. Сколько приблизительно рыб живет в озере?РешениеОказывается, найти ответ на этот неожиданный вопрос совсем несложно. В самом деле: обозначим неизвестную нам численность рыб в озере через N. Тогда вероятность поймать помеченную рыбу в озере будет — 86/N. С другой стороны, эта вероятность должна приближенно равняться полученной во втором улове частоте: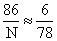Отсюда 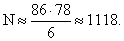Список используемой литературы Видеолекция «Комбинированные задачи»:
Перейти к выполнению теста: Тест. Комбинированные задачи
В начало