Математика: Формулы числа сочетаний. Бином Ньютона

Формулы числа сочетаний. Бином Ньютона

Основные формулы комбинаторики

	Порядок важен		Порядок неважен
Без повторений
С повторениями
	Размещения	Перестановки	Сочетания

Пример 1.Сколько четных двузначных чисел можно составить из цифр 0, 1, 2, 4, 5, 9?Решение:

1-й способ. Выпишем по порядку все числа от 10 до 99 и выберем те, что нам нужны: 10, 12, 14, 20, 22, 24, 40, 42, 44, 50, 52, 54, 90, 92, 94. Всего 15 пар.

2-й способ. Изобразим таблицу вариантов:

	0	2	4
1	10	12	14
2	20	22	24
4	40	42	44
5	50	52	54
9	90	92	94

Всего

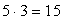чисел.

ПРАВИЛО УМНОЖЕНИЯПусть объекты А и В не зависят друг от друга. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами.В теории вероятностей понятие выборки

обобщается. Вместо него используют понятие испытание

. Поэтому полезно знать правило умножения и на «языке» теории вероятностей

.ПРАВИЛО УМНОЖЕНИЯ:Чтобы найти число всех возможных исходов проведения двух независимых испытаний А и В, надо перемножить число всех исходов испытания А и число всех исходов испытания В.Замечание: Независимость событий А и В означает, что в такой паре (a,b) возможны абсолютно все комбинации исходов этих испытаний: при любом выборе «координаты» a в качестве «координаты» b можно выбрать любой исход события В.3-й способ решения примера 1: Испытание А состоит в выборе первой цифры числа, и у него имеется 5 возможных исходов, а испытание В состоит в выборе второй цифры, и у него имеется 3 возможных исхода. Так как выбор первой цифры независим от выбора второй, то по правилу умножения, всего получается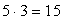

исходов.Ответ: 15.Пример 2.Сколько может быть различных комбинаций выпавших граней при бросании двух игральных костей?Решение:На первой кости может быть: 1,2,3,4,5 и 6 очков, т.е. 6 вариантов (исходов). На второй — 6 вариантов. Бросают и первую, и вторую, значит, применяем правило умножения. Всего:

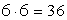вариантов.Ответ: 36.Пример 3.Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 2, 4, 6?Решение: Число всех возможных перестановок цифр 0, 2, 4, 6 будет 4!, но нужно обратить внимание на 0 из этого числа перестановок нужно исключить те числа, которые начинаются с 0. Это всевозможные перестановки цифр 2, 4, 6, их количество равно 3!. Таким образом, число искомых чисел будет равно 4! - 3! = 24 – 6 = 18Ответ: 18.Пример 4.Сколько всего исходов в опыте бросания двух монет одновременно?Решение:При бросании первой монеты возможны два исхода (орел или решка), при бросании второй монеты имеем тоже два исхода (орел или решка). По правилу умножения:

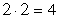.Ответ: 4.Пример 5.Сколько всего исходов, если бросают одну и ту же монету два раза?Решение:При бросании первый раз у монеты возможны два исхода (орел или решка), при бросании второй раз у монеты имеем тоже два исхода (орел или решка). Тогда

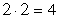.Ответ: 4.Пример 6.Имеется 9 различных книг, 4 из которых — учебники. Сколькими способами можно расставить эти книги на полке так, чтобы все учебники стояли рядом?Решение:Сначала рассмотрим все учебники как одну книгу. Тогда на полке надо расставить не 9, а 6 книг. Это можно сделать Р₆ =6! способами. В каждой из полученных комбинаций можно выполнить Р₄ = 4! перестановок учебников. По правилу умножения независимых событий искомое число способов расположения книг на полке равно произведению

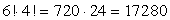.Ответ: 17 280.Пример 7.У Пети есть 7 монет по 1 рублю и 3 монеты по 2 рубля. Петя случайным образом выбирает 1 монету номиналом 1 рубль и 1 монету номиналом 2 рубля. Сколькими способами он может это сделать?Решение:Для начала выясним, сколькими способами Петя может выбрать 1 монету из 7 имеющихся номиналом 1 рубль:

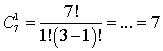.Аналогично, найдем число способов выбрать 1 монету номиналом 2 рубля из имеющихся 3 монет:

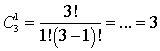.Теперь, согласно закону умножения, найдем общее число способов:

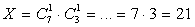.Ответ: 21.Пример 8.В корзине лежат 8 белых шаров и 12 черных. Сколькими способами можно достать из этой корзины 2 белых шара и 2 черных?Решение:Всего в корзине n = 8 белых шаров, из которых надо выбрать k = 2 шара. Это можно сделать C₈² = … = 28 различными способами.Кроме того, в корзине имеется n = 12 черных шаров, из которых надо выбрать опять же k = 2 шара. Число способов сделать это равноC₁₂² = … = 66.Поскольку выбор белого шара и выбор черного — события независимые, общее число комбинаций считается по правилу умножения:28 · 66 = 1848. Как видим, вариантов может быть довольно много.Ответ: 1848.Пример 9.В 10 «Б» классе в среду 7 уроков: алгебра, геометрия, литература, физкультура, русский язык, английский, биология.

А) сколько можно составить различных вариантов расписания на среду?

Б) В скольких расписаниях физкультура будет последним уроком?

В) В скольких вариантах расписания естественно-математические и гуманитарные предметы будут идти блоками, разделенными уроком физкультуры?

Решение:

А) Каждое возможное расписание задает нумерацию семи названных предметов числами 1 2 3 4 5 6 7 в соответствии с порядковым номером урока. Таких нумераций всего 7! = 5040.

Б) 6 уроков (кроме физкультуры) надо распределить по номерам 1 - 6. Всего имеется 6! =720 вариантов.

В) Физкультуру следует поставить 4-м уроком. Расписание будет составлено, как только мы проведем следующие три независимых испытания.

Во-первых, выбор блока (1-й - 3-й или 5-й – 7-й уроки) для гуманитарных предметов. Тут возможны 2 исхода: поставить этот блок до урока физкультуры или после него. Алгебра, геометрия и биология автоматически окажутся в другом блоке.

Во-вторых, выбор порядка гуманитарных предметов в уже выбранном блоке: Р3 = 3! = 6 различных перестановок.

В-третьих, следует посчитать и все перестановки для естественно-математических предметов — их тоже 6. По правилу умножения получаем:

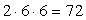
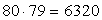Ответ: 72.Пример 10.Собрание из 80 человек выбирает председателя, секретаря и трех членов редакционной комиссии. Сколькими способами это можно сделать?Решение:Председателем может быть любой из участников собрания — 80 вариантов. Если председатель выбран, секретарем может оказаться любой из оставшихся 79 человек — 79 вариантов. По правилу умножения получим ( в предположении независимости выбора секретаря и председателя), что выбор председателя и секретаря осуществляется

способами.Если испытание А — выбор председателя и секретаря — завершено, то следует заняться испытанием В — выбором трех членов комиссии из оставшихся 78 участников собрания. Редакционную комиссию выбирают списком, т.е. порядок отбора не имеет значения. Сделать это можно С₇₈³способами. Имеем:

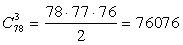. Поскольку А и В предполагаются независимыми, применим правило умножения:

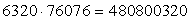способов.Ответ: 480 800 320.Пример 11.Сколько существует всего исходов, если друг за другом из колоды вынимают три карты, возвращая карту обратно (выбор с возвращением).Решение:Для первой карты возможно 36 возможностей выбора. Когда первую карту вытащили, то положив ее обратно, в колоде стало снова 36 карт, значит для второй карты тоже 36 возможных исходов. Для третьей карты все то же самое. По правилу умножения имеем n = 36 · 36 · 36 = 46 656.Ответ: 46 656.Пример 12.Из 3-х экземпляров учебника алгебры, 7-ми экземпляров учебника геометрии, 6-ти экземпляров учебника физики надо выбрать один комплект, содержащий все три учебника по одному разу. Сколькими способами это можно сделать?Решение:Пусть А — «выбор 1 учебника алгебры», N(A)=3, В — «выбор 1 учебника геометрии», N(B)=7, С — «выбор 1 учебника физики», N(C)=6. Применяя правило умножения, получим: 3·7·6=126 способов.Ответ: 126.ПРАВИЛО СЛОЖЕНИЯ:Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то

выбрать либо А, либо В можно (m + n) способами, если А и В не имеют общих элементов.
выбрать либо А, либо В можно (m + n – d) способами, если А и В имеют d общих элементов.

Другими словами, при объединении взаимоисключающих действий

число их комбинаций складывается.Если правило умножения оперирует «изолированными» событиями, которые не зависят друг от друга, то в правиле сложения все наоборот. Здесь рассматриваются взаимоисключающие события, которые никогда не случаются одновременно.Например, «Петя вынул из кармана 1 монету» и «Петя не вынул из кармана ни одной монеты» — это взаимоисключающие события, поскольку вынуть одну монету и при этом не вынуть ни одной невозможно.Аналогично, события «Выбранный наугад шар — белый» и «Выбранный наугад шар — черный» также являются взаимоисключающими.Можно сказать, что закон сложения — это логическое «ИЛИ» в комбинаторике, когда нас устраивает любой из взаимоисключающих вариантов. И наоборот, закон умножения — это логическое «И», при котором нас интересует одновременное выполнение и первого, и второго действия.Пример 13.В коробке находится 10 шаров: 3 белых, 2 черных, 1 синий и 4 красных. Сколькими способами можно взять из ящика цветной шар?Решение:Цветной шар — это синий или красный. Выбрать синий можно одним способом, а выбрать красный шар — 4 варианта, поэтому по правилу сложения: 1 + 4 = 5 способов.Ответ: 5.Пример 14.Из 20 вопросов к экзамену ученик 12 выучил, 5 совсем не смотрел, а в остальных что-то знает, а что-то нет. На экзамене будет три вопроса.

а) Найти количество возможных вариантов билета.

б) Сколько из них тех, в которых ученик знает все вопросы?

в) Сколько из них тех, в которых есть вопросы всех трех типов?

г) Сколько из них тех, в которых ученик выучил большинство вопросов?

Решение:

а) Порядок вопросов в билете не важен. Поэтому возможны

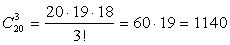вариантов билета.

б) Тут все три вопроса надо выбирать из тех 12, которые выучил ученик:

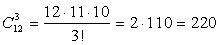в) Билет подобного типа составляется так: следует выбрать независимо друг от друга по одному вопросу – из блока выученных 12 вопросов, из блока тех 5-ти, что он не смотрел и из оставшихся 3-х вопросов. По правилу умножения получим: 12·5·3 = 180.

г) Большинство вопросов из трех – это два или три. Выбрать два из 12 выученных вопросов и один из оставшихся 8 вопросов можно (по правилу умножения)

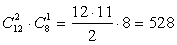способами. А билеты, в которых все вопросы выучены, уже посчитаны в пункте б), их всего 220. В итоге, применяя правило сложения, получим 528 + 220 = 748 билетов.

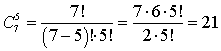Ответ: а) 1140, б) 220, в) 180, г) 748.Пример 15.Из класса нужно выделить одного дежурного, мальчика или девочку. Сколько существует способов для выбора дежурного, если в классе 22 девочки и 18 мальчиков?Решение:Выбрать одну девочку из 22 мы можем 22 способами, а одного мальчика из 18 можно 18 способами. Тогда выбрать одного дежурного мальчика или девочку можно 18 + 22 = 40 способами.Ответ: 40.Пример 16.В классе из 25 человек 19 красивых и 13 умных. Все дети являются или (и) красивыми, или (и) умными. Сколькими способами можно выбрать 5 человек среди красивых и умных?Решение:Пусть Х – количество и красивых и умных, тогда применим 2-ю формулу сложения: 25 = 19 + 13 – Х, откуда найдем Х = 32 – 25 = 7 человек и красивых и умных. Порядок не важен, тогда

.Ответ: 21.Пример 17.В корзине лежат 9 черных шаров и 7 красных. Мальчик достает 2 шара одинакового цвета. Сколькими способами он может это сделать?Решение:Если шары одинакового цвета, то вариантов немного: оба они либо черные, либо красные. Очевидно, что эти варианты — взаимоисключающие.В первом случае мальчику предстоит выбирать k = 2 черных шара из n = 9 имеющихся. Число способов сделать это равно C₉² = … = 36.Аналогично, во втором случае выбираем k = 2 красных шара из n = 7 возможных. Число способов равно C₇² = … = 21.Осталось найти общее количество способов. Поскольку варианты с черными и красными шарами — взаимоисключающие, по закону сложения имеем: X = 36 + 21 = 57.Ответ: 57Пример 18.В ларьке продаются 15 роз и 18 тюльпанов. Ученик 9-го класса хочет купить 3 цветка для своей одноклассницы, причем все цветы должны быть одинаковыми. Сколькими способами он может составить такой букет?Решение:По условию, все цветы должны быть одинаковыми. Значит, будем покупать либо 3 розы, либо 3 тюльпана. В любом случае, k = 3.В случае с розами придется выбирать из n = 15 вариантов, поэтому число сочетаний равно C₁₅³ = … = 455. Для тюльпанов же n = 18, а число сочетаний — C₁₈³ = … = 816.Поскольку розы и тюльпаны — это взаимоисключающие варианты, работаем по закону сложения. Получаем общее число вариантов X = 455 + 816 = 1271. Это и есть ответ.Ответ: 1271.Пример 19.Встретились 11 футболистов и 6 хоккеистов и стали играть друг с другом по одному разу в шашки. Сколько было встреч:

а) между футболистами,

б) между хоккеистами,

в) между теми и другими,

г) всего?

Решение:

а)

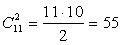б)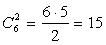

в) Тут надо действовать по правилу умножения. Одно испытание — выбор футболиста, а другое испытание — выбор хоккеиста. Испытания предполагаются независимыми, и у них соответственно 11 и 6 исходов. Значит, получится 11 · 6 = 66 игр.

г) Можно сложить все предыдущие ответы: 55 + 15 + 66 = 136, но можно использовать формулу:

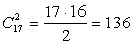Дополнительные условия и ограниченияОчень часто в тексте задачи присутствуют дополнительные условия, накладывающие существенные ограничения на интересующие нас сочетания. Сравните два предложения:

Имеется набор из 5 ручек разных цветов. Сколькими способами можно выбрать 3 ручки для обводки чертежа?
Имеется набор из 5 ручек разных цветов. Сколькими способами можно выбрать 3 ручки для обводки чертежа, если среди них обязательно должен быть красный цвет?

Чувствуете разницу? В первом случае мы вправе брать любые цвета, какие нам нравятся — дополнительных ограничений нет. Во втором случае все сложнее, поскольку мы обязаны выбрать ручку красного цвета (предполагается, что она есть в исходном наборе).Очевидно, что любые ограничения резко сокращают итоговое количество вариантов. Ну и как в этом случае найти число сочетаний? Просто запомните следующее правило:Пусть имеется набор из n элементов, среди которых надо выбрать k элементов. При введении дополнительных ограничений числа n и k уменьшаются на одинаковую величину.Другими словами, если из 5 ручек надо выбрать 3, при этом одна из них должна быть красной, то выбирать придется из n = 5 – 1 = 4 элементов по k = 3 – 1 = 2 элемента. Таким образом, вместо C₅³ надо считать C₄².Теперь посмотрим, как это правило работает на конкретных примерах:Пример 20.В группе из 20 студентов, среди которых 2 отличника, надо выбрать 4 человека для участия в конференции. Сколькими способами можно выбрать этих четверых, если отличники обязательно должны попасть на конференцию?Решение:Итак, есть группа из n = 20 студентов. Но выбрать надо лишь k = 4 из них. Если бы не было дополнительных ограничений, то количество вариантов равнялось числу сочетаний C₂₀⁴.Однако нам поставили дополнительное условие: 2 отличника должны быть среди этих четырех. Таким образом, согласно приведенному выше правилу, мы уменьшаем числа n и k на 2. Имеем:

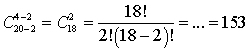.Ответ: 153.Пример 21.У Пети в кармане есть 8 монет, из которых 6 монет по рублю и 2 монеты по 10 рублей. Петя перекладывает какие-то три монеты в другой карман. Сколькими способами Петя может это сделать, если известно, что обе монеты по 10 рублей оказались в другом кармане?Решение:Итак, есть n = 8 монет. Петя перекладывает k = 3 монеты, из которых 2 — десятирублевые. Получается, что из 3 монет, которые будут переложены, 2 уже зафиксированы, поэтому числа n и k надо уменьшить на 2. Имеем:

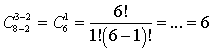.Ответ: 6.Бином НьютонаБином Ньютона

— это формула, представляющая выражение ( a + b )ⁿ при положительном целом n в виде многочлена: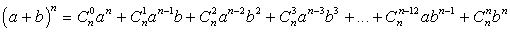

.Заметим, что сумма показателей степеней для a и b постоянна и равна n.Числа С_n⁰,C_n¹, C_n², …, C_n-1ⁿназываются биномиальными коэффициентами

.Запишем известные нам формулы в виде: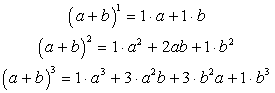

Знаком умножения отделены числовые коэффициенты при одночленах. Заметим, что 1 = С₃⁰, 3 = С₃¹, 3 = С₃², 1 = С₃³ (в формуле куба суммы).Для чисел С_n^k имеется красивый и удобный способ их записи в виде треугольной таблицы. Ее называют треугольником Паскаля:

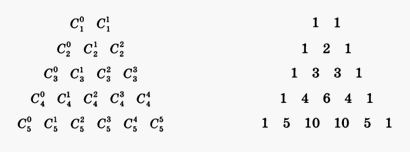Их можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки.Некоторые биномиальные формулы полезно запомнить:

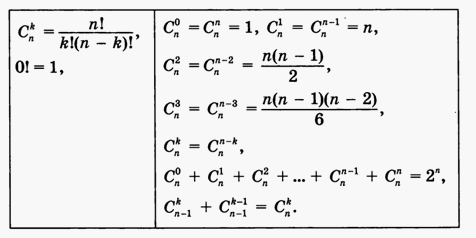Замечание. Сумма коэффициентов в разложении (a + b )n равна 2n.Пример 22.Разложить выражение: ( a + b )⁷.Мы можем получить результат моментально, используя таблицу: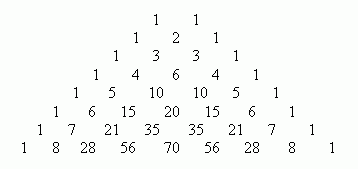

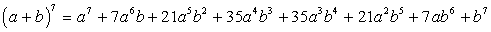Для того чтобы получит формулу бинома Ньютона для 3-х и более слагаемых в скобках, необходимо вспомнить формулы комбинаторики, использующие повторения.Пример 23.Сколькими способами можно разложить 28 различных предметов по четырем различным ящикам, так, чтобы в каждом ящике, оказалось, по 7 предметов?Решение:

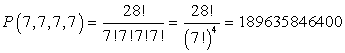способов.Ответ: 189 635 846 400.В примере 11 было существенно, что ящики можно отличить друг от друга (например, они покрашены в разные цвета).Пример 24.Сколькими способами можно положить 28 различных открыток в 4 одинаковых конверта так, чтобы в каждом конверте лежало по 7 открыток?Решение:Сначала пометим конверты цифрами 1, 2, 3, 4. Тогда согласно примеру 18 число различных раскладок равно P(7,7,7,7). После этого сотрем пометки. Теперь конверты можно произвольным образом переставлять друг с другом, не меняя результата раскладки (ведь теперь они неотличимы друг от друга). Так как число различных перестановок четырех конвертов равно Р4 = 4!, то число раскладок уменьшается в 4! Раз, и потому оно равно

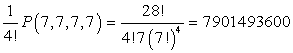Ответ: 7 901 493 600.Легко доказать, используя в формулу числа сочетаний, что C_n^k=C_n^n-k.Заметим, что так как

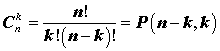,То формулу бинома Ньютона можно записать следующим образом:

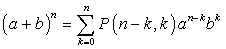.Такая запись обобщается на случай большего числа слагаемых в скобке. Именно для любых k и t верна формула

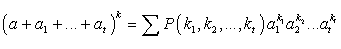,где сумма распространяется на все числовые кортежи (k₁,k₂,…,k_n ) из неотрицательных целых чисел, такие, что k=k₁ + k₂ + … + k_t .Замечание. Сумма коэффициентов в разложении (a₁ + a₂ + … + a_t)k равна t^k.Пример 25.Раскрыть скобки в выражении (a+b+c)³.Решение:Ответ имеет вид:

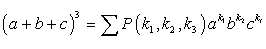,где сумма распространяется на все кортежи (k₁,k₂,k₃ ) такие, что 3=k₁ + k₂ + k₃ .Ими являются кортежи (3,0,0,), (0,3,0), (0,0,3), (2,1,0), (2,0,1), (1,2,0), (1,0,2), (0,1,2), (0,2,1), (1,1,1). Так как

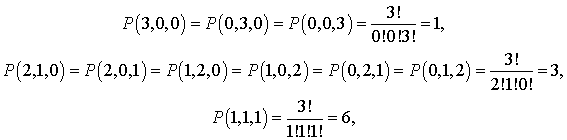то получим ответ:

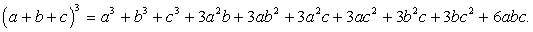Пример 26.Найти сумму коэффициентов в разложении (a + b + c)⁴.Решение:Зная, что сумма коэффициентов в разложении (a + b + c)⁴ равна 3⁴=81.Ответ: 81.Пример 27.Найти сумму коэффициентов в разложении (a + b + c + d)⁵.Решение:Зная, что сумма коэффициентов в разложении (a + b + c + d)⁵ равна 4⁵ = 1024.Ответ: 1024.Список используемой литературы Видеолекция «Формулы числа сочетаний. Бином Ньютона»:

Перейти к выполнению теста: Тест. Формулы числа сочетаний. Бином Ньютона