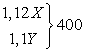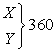Комбинированные задачи
Решение:Задача сводится к решению неравенства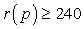 
:
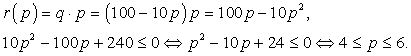Так как требуется максимальный уровень цены, при котором месячная выручка составит не менее 240 тыс. руб., то выбираем значение р = 6.Ответ: 6.Пример 2.В боковой стенке высокого цилиндрического бака у самого дна закреплен кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону:
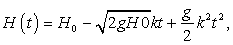где t — время в секундах, прошедшее с момента открытия крана, H0 = 20 м — начальная высота столба воды, k = 1/50 — отношение площадей поперечных сечений крана и бака, а g — ускорение свободного падения (считайте g = 10 м/с2).Через сколько секунд после открытия крана в баке останется четверть первоначального объема воды?Решение:Для начала выясним, чему равно искомое H(t). По условию, в баке должна остаться четверть первоначального объема воды. Поэтому H(t) = (1/4) 20 = 5 м.Теперь, когда все параметры известны, подставим числа в функцию:
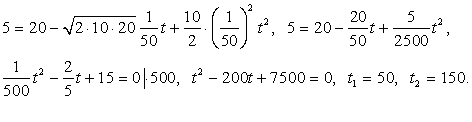Итак, у нас два кандидата на ответ: числа 50 и 150. Заметим, что в момент времени t = 100 высота столба воды равна:
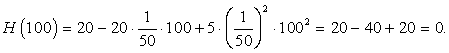Другими словами, через t = 100 секунд вода полностью вытечет из бака, и уравнение H(t) теряет физический смысл. Поэтому вариантt = 150 нас не интересует. Остается только t = 50.Ответ: 50.Рассмотрим задачу с геометрическим содержанием.Пример 3.От вершины прямого угла по его сторонам одновременно начинают движение две материальные точки со скоростями 5 см/с и 12 см/с. Через какое время расстояние между ними станет 52 см?Решение:
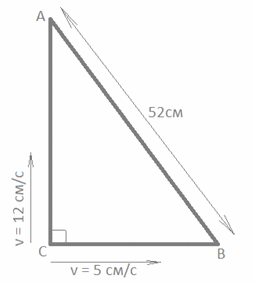Применим теорему Пифагора к условию задачи:
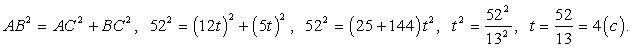Ответ: 4.Следующую задачу по условию можно отнести к задачам «на работу», а по решению — к задачам «на числа и проценты».Пример 4.Два завода по плану должны были выпустить за месяц 360 станков. Первый завод выполнил план на 112%, а второй— на 110%, вместе заводы выпустили за месяц 400 станков. Сколько станков сверх плана выпустил каждый завод в отдельности?Решение:Пусть Х станков должен выпустить первый завод, а У — второй.
|
По плану |
Фактически |
Первый завод |
|
|
Второй завод |
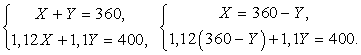Решим второе уравнение: 403,2 - 1,12У +1,1У = 400; 3,2 = 0,02У; У = 160.Тогда Х = 360 – 160 =200. Итак, первый завод по плану должен выпустить 200 станков, а второй завод – 160. Но в задаче спрашивается сколько станков сверх плана выпустил каждый из заводов. Первый завод выпустил на 12% больше, чем по плану, т.е. 200·0,12 = 24 станка, второй на 10% перевыполнил план, т.е. 160·0,1 =16 станков.Ответ: 24, 16.Следующая задача сочетает в себе такие типы задач как «на совместную работу и производительность» и «на проценты».Пример 5.На угольной шахте сначала работали два участка, а через некоторое время вступил в работу третий участок. В результате производительность труда повысилась на 50%. Сколько процентов составляет производительность 2-го участка от производительности 1-го участка, если за 4 месяца работы 1-й и 3-й участки выдают угля столько же, сколько 2-й участок за 1 год.Решение:Пусть V1 , V2 , V3 — производительности соответственно 1-го, 2-го и 3-го участков. Составим систему уравнений, опираясь на условие задачи:
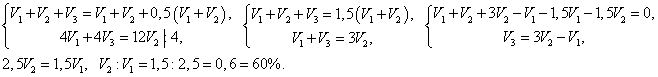Ответ: 60%.Следующая задача на первый взгляд кажется задачей на движение навстречу, но решается она немного сложнее.Следующую задачу разберем, т.к. она не вошла ни в один из изученных типов.Пример 6.За самостоятельную работу ученикам выставили оценки: «2», «3», «4», «5». Оценки «2», «3» и «5» получили одинаковое число учеников, а «4» поставлено больше, чем всех остальных, вместе взятых. Оценки выше «3» получили менее 10 учеников. Сколько «3» и сколько «4» было поставлено, если писали работу не менее 12 учеников и каждый писавший получил оценку?Решение:Пусть число учеников, получивших оценку «2» — x, «3» — y, «4» — z, «5» — t. Тогда получим систему неравенств и уравнений:
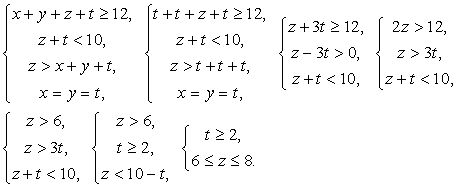Пусть t =2, тогда z =7. Проверим, подставив во вторую систему: 
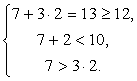Итак, оценки «2», «3» и «5» получили по 2 ученика, «4» — 7 учеников.Ответ: 2,7.В следующей задаче встретились три типа задач сразу: «движение по окружности», «движение навстречу», «движение вдогонку».Пример 7.По окружности, имеющей длину 1350 м, в одном направлении едут два велосипедиста. Первый обгоняет второго каждые 27 минут. При движении в противоположных направлениях они встречаются каждые 3 минуты. Найти скорости велосипедистов (в км/ч).Решение:Пусть v1 и v2 — скорости велосипедистов. За 27 мин = 0,45ч они проедут пути соответственно 0,45v1 км и 0,45v2 км. Причем первый проедет на длину окружности (1350 м = 1,35 км) больше второго, т.е.0,45v1 - 0,45v2 =1,35|:0,45.За 3 мин = 0,05ч они проедут пути соответственно 0,05v1 км и 0,05v2 км. А вместе они проедут расстояние, равное длине полной окружности, т.е. 0,05v1 + 0,05v2 =1,35|:0,05.
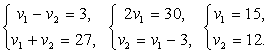Итак, скорость первого велосипедиста 15 км/ч, второго — 12 км/ч.Ответ: 15,12.Пример 8.Мальчики составляют 45% всех учащихся школы. Известно, что 30% маль-чиков и 40% девочек учатся без троек. Сколько процентов всех учащихся школы учатся без троек?Решение:Пусть в школе х учащихся. Тогда в ней 0,45х мальчиков и 0,55х девочек. Без троек учатся 0,3·0,45х = 0,135х мальчиков и 0,4·0,55х = 0,22х девочек. А всего 0,135х + 0,22х = 0,355х. Или 35,5% учащихся школы учатся без троек.Ответ: 35,5.Пример 9.В одном государстве правительство вынесло на всенародное голосова-ние проект закона о запрете рекламы спиртных напитков. Этот проек поддержали 69% всего взрослого населения, принявшего участие в голосовании, причем среди женщин 94%, а среди мужчин 41%. Кого среди голосовавших было больше: мужчин или женщин?Решение:Пусть в голосовании приняли участие х женщин и у мужчин. Постановление поддержали 0,94х женщин и 0,41у мужчин, а всего 0,69(х + у) человек: 0,94х + 0,41у = 0,69(х + у). Раскроем скобки и приведем подобные слагаемые: 0,25х = 0,28у. Отсюда следует, что х > у.Ответ: женщин было больше.Пример 10.Сын младше отца в 7 раз, а через год он станет младше отца в 6 раз. Через сколько лет сын станет младше отца в 4 раза?Решение:Если возраст сына равен Х, то возраст отца равен 7Х, и через год им будет соостветственно Х + 1 и 7Х + 1 лет. По условию задачи, 7Х + 1 = 6(Х + 1), откуда Х = 5, 7Х = 35. Если сын станет младше отца в 4 раза через n лет, то 35 + n =4(5 + n), откуда n = 5.Ответ: 5.Пример 11.Сыну 2 года, а отцу 28 лет. Сколько еще раз в течение их жизни сын будет младше отца в целое число раз, если отец проживет ровно 100 лет?Решение:Каждый раз, когда сын младше отца в целое число k раз, разность их возрастов также в целое число раз больше возраста сына, и поэтому требуется найти, сколько существует натуральных чисел от 2 до 72, при которых число k + 2 является делителем числа 26. Так как 26 имеет 2 делителя, больших 2 (13 и 26), то событие, о котором идет речь в условии задачи, случится 2 раза.Ответ: 2.Пример 12.Группа из 30 студентов на экзамене получила оценки «2», «3», «4», «5», причем общая сумма баллов равнялась 93. Троек было больше, чем пятерок, и меньше, чем четверок. Число четверок делилось на 10, число пятерок было четным. Сколько пятерок было получено?Решение:Из условия следует, что вклад четверок в общую сумму равен либо 40, либо 80. Но вклад пятерок не меньше 10, а так как троек больше, чем пятерок, то их вклад не меньше 9, и общая сумма не меньше 99, что неверно, так что четверок 10, а тогда пятерок 2, 4, 6 или 8.Если пятерок 8, то троек 9, а 40 + 27 + 40 > 93, что опять неверно. Если их 6, то вклад двоек и троек равен 23, но троек не меньше 7, тогда их ровно 7, а двойка одна. Но общее число оценок в этом случае равно 1 + 7 + 10 + 6 = 24, что неверно, так что число пятерок не равно 6.Если пятерок 4, то то вклад двоек и троек равен 33, вместе их 30 – 10 – 4 = 16, причем троек не меньше 5. Если их 5, то двоек 11, и общий вклад двоек и троек равен 27, а при каждом увеличении числа троек на 1 и соответствующем уменьшении на 1 числа двоек получатся вклады 28, 29, 30, 31, меньшие 33.Следовательно пятерок было получено 2.Ответ: 2.Пример 13.Имеются путевки трех типов, которые стоят соответственно 4,6 и 9 неразменных батов. Путевка 1-го типа расчитана на 8 дней, второго — на 14, и 3-го — на 20 дней отдыха. Сколько путевок каждого типа можно купить на 100 батов, чтобы общее число дней было наибольшим?Решение:За 36 батов можно купить соответственно 9, 6 и 4 путевок разных типов, а отдохнуть соотвественно 72, 84 и 80 дней. Так что по «убыванию выгодности» типы путевок располагаются так: 2-й, 3-й, 1-й.Поэтому вместо 3 путевок 1-го типа на те же деньги можно купить 2 путевки 2-го типа и тем самым увеличить число дней отдыха. Иными словами, в нужной покупке число путевок 1-го типа не больше 2. Точно так же на 18 батов можно купить 3 путевки 2-го типа или 2 путевки 3-го типа. Однако второй вариант хуже, так что путевок 3-го типа надо покупать не более одной. Но если купить одну, то на осталь-ные путевки придется 91 батов, а это число нечетно, тогда как каждая из этих путевок стоит четное число батов, так что путевок 3-го типа вообще не следует покупать.Поэтому на 100 батов надо как можно больше купить путевок 2-го типа, а поскольку их стоимость должна делиться на 6, то их нужно купить 16, а на оставшиеся 4 бата — одну путевку 1-го типа.Ответ: 16 путевок 2-го типа и одну — 1-го.Пример 14.На факультет от выпускников лицеев подано на 600 заявлений больше, чем от выпускников гимназий. Девушек среди выпускников лицеев в 5 раз больше, чем девушек среди выпускников гимназий. А юношей среди выпускников лицеев больше, чем юношей среди выпускников гимназий в n раз, причем 6 < n < 12 (n - целое число). Определить общее количество заявлений, если среди выпускников гимназий юношей на 20 больше, чем девушек.Решение:Обозначим число девушек-гимназисток через Х и заполним таблицу:
Девушки -гимназистки |
Юноши-гимназисты |
Девушки из лицея |
Юноши из лицея |
Х |
Х + 20 |
5Х |
n (X + 20) |
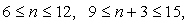а 680 = 17·2·2·5.Как нетрудно заметить, имеет место только один делитель от 9 до 15 — число 10, так что n =7, X + 20 = 680 :10 = 68, Х = 48.Общее число заявлений равно 7Х + 20 + 7(Х + 20) = 14·18 + 160 = 832.Ответ: 832.Пример 15.Абитуриенты в течение трех дней сдавали экзамены в одних и тех же аудиториях. Число абитуриентов, экзаменовавшихся каждый день в каждой из ау-диторий, было равным чуслу аудитроий. Если бы экзамены проводились в другом корпусе, то их можно было бы провести за 2 дня, используя каждый день одни и те же аудитории, причем каждый день в каждой аудитории абитуриентов удалось бы рассадить по рядам так, что число рядов, а также число людей в ряду было бы равным числу используемых аудиторий. Найти минимальное возможное число абитуриентов, которое могло быть проэкзаменовано при этих условиях.Решение:Пусть Х и У — число аудиторий в первом и втором корпусах. Тогда в каждой аудитории экзаменовалось Х абитуриентов, так что всего абитуриентов было 3Х2, а во втором варианте проведения экзамена в каждой из У аудиторий экзаменовалось бы У2 человек, и следовательно, абитуриентов было 2У3, и таким образом, 3Х2 = 2У3.Отсюда следует, что Х делится на 2, а У делится на 3, т.е.Х = 2a, Y = 3b, 12 a3 = 54 b3, 2a2 = 9b3,a = 3c, b = 1d, 18c2 = 72d3 , c2 = 4d3,c = 2p, 4p2 = 4d3, p2 = d.Наименьшие числа, удовлетворяющие этому равенству — это р = d = 1. Далее получаем с = 2, a = 6, Х = 12, 3Х2 = 432.Ответ: 432.Пример 16.В конференции принимает участие 77 человек. Может ли каждый из них быть знаком ровно с семью другими?Решение:Перенумеруем мысленно всех участников конференции и сделаем «список знакомств», а «знакомством» будем считать пару чисел, являющихся номерами людей, знакомых друг с другом. Список организуем так: сначала пойдут семь «знакомств» первого по порядку участника, затем семь «знакомств» второго и т.д. Так как каждый человек знаком ровно с семью другими, то всего имеется 77·7 «знакомств», но каждое «знакомство» в этом списке появится ровно 2 раза — так как мы не считаем человека «знакомым с самим собой», то в каждой паре номера различны. Поэтому число 77·7 должно делиться на 2, а это неверно. Значит, ситуация, описанная в задаче невозможна.Ответ: не может.Список используемой литературы Видеолекция «Комбинированные задачи»: 
