Задания с параметром
 :
:- 1) Найти все значения параметра, при каждом из которых выполняется определенное условие;2) Решить уравнение или неравенство с параметром a.
 в заданиях с параметром
в заданиях с параметром- А)
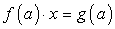 ,При
,При 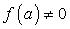 - решение
- решение 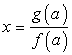 ;При f(a) = 0,
;При f(a) = 0, 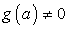 - решений нет;При f(a) = 0, g(a) = 0 -решений бесконечно много
- решений нет;При f(a) = 0, g(a) = 0 -решений бесконечно много 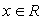 .Б)
.Б) 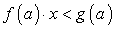 ,При f(a) > 0 -
,При f(a) > 0 - 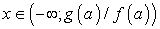 ;При f(a) < 0 -
;При f(a) < 0 - 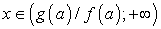 ;При f(a) = 0, g(a) < 0 - решений нет;При f(a) = 0, g(a) > 0 - решений бесконечно много
;При f(a) = 0, g(a) < 0 - решений нет;При f(a) = 0, g(a) > 0 - решений бесконечно много 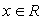 .
.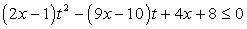 не имеет решений. Если таких значений несколько, то найти их сумму.Решение:Это линейное неравенство относительно «х». Раскроем скобки и вынесем его за скобки:
не имеет решений. Если таких значений несколько, то найти их сумму.Решение:Это линейное неравенство относительно «х». Раскроем скобки и вынесем его за скобки: 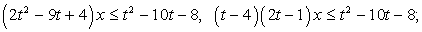
- 1) Если (t - 4)(2t - 1) > 0, то решение
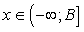 , где
, где 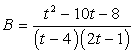 ;2) Если (t - 4)(2t - 1) < 0, то решение
;2) Если (t - 4)(2t - 1) < 0, то решение 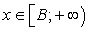 ;3) Если (t - 4)(2t - 1) = 0, тоПри t = 4,
;3) Если (t - 4)(2t - 1) = 0, тоПри t = 4, 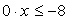 , нет решений,При t =
, нет решений,При t = 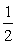 ,
,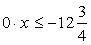 , нет решений
, нет решений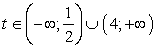 , то
, то 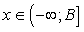 , где
, где 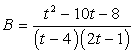 ;при
;при 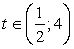 , то
, то 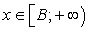 , при t =
, при t = 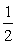 или при t = 4 решений нет.Нас интересует случай, когда решений нет, тогда 4 +
или при t = 4 решений нет.Нас интересует случай, когда решений нет, тогда 4 + 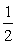 = 4,5.Ответ: 4,5.Пример 2.Найти все значения параметра t, при которых система имеет 2012 решений. Если таких значений несколько, то найти их сумму.
= 4,5.Ответ: 4,5.Пример 2.Найти все значения параметра t, при которых система имеет 2012 решений. Если таких значений несколько, то найти их сумму.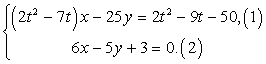 Решение:(1) и (2) — это линейные уравнения относительно двух переменных. Каждое из уравнений является уравнением прямой. Если прямые пересекаются, то система имеет единственное решение. Если прямые совпадают, то решений бесконечно много или, например, 2012 штук.Выразим из (2) 5у и подставим в (1), получим:
Решение:(1) и (2) — это линейные уравнения относительно двух переменных. Каждое из уравнений является уравнением прямой. Если прямые пересекаются, то система имеет единственное решение. Если прямые совпадают, то решений бесконечно много или, например, 2012 штук.Выразим из (2) 5у и подставим в (1), получим: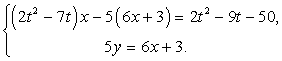 Продолжим решать первое уравнение:
Продолжим решать первое уравнение: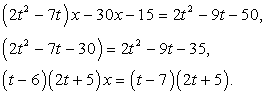 Из последнего уравнения видно, что система имеет бесконечно много решений, когда 2t + 5 = 0, т.е. t = -2,5.Заметим, что при t = 6 или t =7 решений нет.Ответ: -2,5.Квадратичная функция в заданиях с параметром.Уравнение вида Ах2 + Вх + С = 0, где А, В, С — выражения, зависящие от параметров,
Из последнего уравнения видно, что система имеет бесконечно много решений, когда 2t + 5 = 0, т.е. t = -2,5.Заметим, что при t = 6 или t =7 решений нет.Ответ: -2,5.Квадратичная функция в заданиях с параметром.Уравнение вида Ах2 + Вх + С = 0, где А, В, С — выражения, зависящие от параметров, 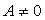 , х — переменная, называется квадратным уравнением с параметрами
, х — переменная, называется квадратным уравнением с параметрами .Во множестве действительных чисел это уравнение исследуется по следующей схеме.
.Во множестве действительных чисел это уравнение исследуется по следующей схеме.- 1) Если А = 0, то имеем линейное уравнение Вх + С =0.2) Если
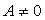 дискриминант D = В2 – 4АС < 0, то уравнение решений не имеет.3) Если
дискриминант D = В2 – 4АС < 0, то уравнение решений не имеет.3) Если 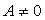 дискриминант D = 0, то уравнение имеет единственное решениех = -В/(2А).4) Если
дискриминант D = 0, то уравнение имеет единственное решениех = -В/(2А).4) Если 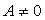 дискриминант D = В2 – 4АС > 0, то уравнение имеет два корня
дискриминант D = В2 – 4АС > 0, то уравнение имеет два корня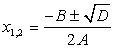 .
.- а) имеет два корня;б) не имеет корней;в) имеет один корень.
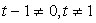 . Рассмотрим дискриминант: D = 4(2t + 1)2 – 4(t - 1)(4t + 3) = 4(5t + 4).Согласно схеме исследования, имеем:Ответ: а) при t > -4/5 t ≠ 1 два корня; б) при t < -4/5 нет корней; в) при t = -4/5 один корень.Пример 4.Найти наибольшее целое значение параметра t, для которого выполняется неравенство: (1-t)x2+3x-t-1>0.Решение:В левой части неравенства квадратный трехчлен, который будет всегда положительным при ветвях параболы, направленных вверх (т.е. 1 – t > 0 или t < 1) и отрицательном дискриминанте:D=9+4(1-t)(t+1)<0, D=13-4t2=-4(t2-13/4)<0.
. Рассмотрим дискриминант: D = 4(2t + 1)2 – 4(t - 1)(4t + 3) = 4(5t + 4).Согласно схеме исследования, имеем:Ответ: а) при t > -4/5 t ≠ 1 два корня; б) при t < -4/5 нет корней; в) при t = -4/5 один корень.Пример 4.Найти наибольшее целое значение параметра t, для которого выполняется неравенство: (1-t)x2+3x-t-1>0.Решение:В левой части неравенства квадратный трехчлен, который будет всегда положительным при ветвях параболы, направленных вверх (т.е. 1 – t > 0 или t < 1) и отрицательном дискриминанте:D=9+4(1-t)(t+1)<0, D=13-4t2=-4(t2-13/4)<0.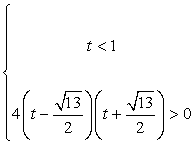 Изобразим решения системы на числовой прямой:
Изобразим решения системы на числовой прямой: 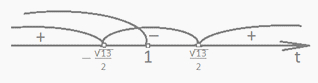 Все решения неравенства:
Все решения неравенства: 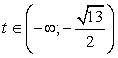 . Наибольшее целое число
. Наибольшее целое число 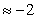 , т.к.
, т.к. 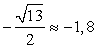 .Ответ: -2.Применение свойств функций и производной в задачах с параметром. Графический метод.Чтобы найти все значения параметра t, при которых уравнение f(x) = g(t) разрешимо (т.е. имеет хотя бы одно решение), надо:
.Ответ: -2.Применение свойств функций и производной в задачах с параметром. Графический метод.Чтобы найти все значения параметра t, при которых уравнение f(x) = g(t) разрешимо (т.е. имеет хотя бы одно решение), надо:- 1) найти множество значений функции f(x), когда х пробегает область определения функции,2) потребовать, чтобы значения функции g(t) менялись на этом множестве.
- а) 4 корня;б) 3 корня;в) 2 корня;г) 1 корень;д) не имеет корней.
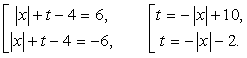 Построим график:
Построим график: 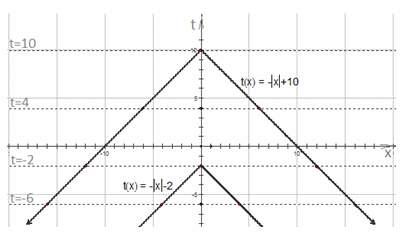 Проводя прямые вида t = k параллельно оси ОХ, определяем количество корней уравнения.
Проводя прямые вида t = k параллельно оси ОХ, определяем количество корней уравнения.- Ответ: а) при
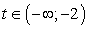 уравнение имеет 4 корня;б) при t = -2 уравнение имеет 3 корня;в) при
уравнение имеет 4 корня;б) при t = -2 уравнение имеет 3 корня;в) при 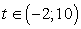 уравнение имеет 2 корня;г) при t = 10 уравнение имеет один корень;д) при
уравнение имеет 2 корня;г) при t = 10 уравнение имеет один корень;д) при 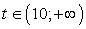 уравнение не имеет корней.
уравнение не имеет корней.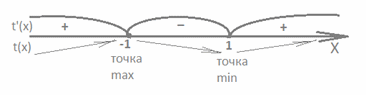 На основании полученных результатов построим график:
На основании полученных результатов построим график: 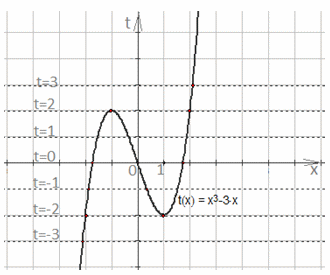 Проводя прямые t = k, определим число решений данного уравнения.Ответ: при
Проводя прямые t = k, определим число решений данного уравнения.Ответ: при  одно решение; при t = ±2 два решения; при
одно решение; при t = ±2 два решения; при  три решения.Пример 7.Для всех значений параметра t решить уравнение |x2 – 4x|- 6t = 0.Решение:Заданное уравнение является линейным относительно параметра t. Построим график функции t=1/6 |x2-4x|. Для этого найдем вершину параболы: х0= 2/3 и точки, в которых парабола пересекает ось ОХ: х1 = 0, х2 = 4. Далее, используя преобразования графиков с модулем, отображаем часть параболы относительно оси симметрии ОХ.
три решения.Пример 7.Для всех значений параметра t решить уравнение |x2 – 4x|- 6t = 0.Решение:Заданное уравнение является линейным относительно параметра t. Построим график функции t=1/6 |x2-4x|. Для этого найдем вершину параболы: х0= 2/3 и точки, в которых парабола пересекает ось ОХ: х1 = 0, х2 = 4. Далее, используя преобразования графиков с модулем, отображаем часть параболы относительно оси симметрии ОХ.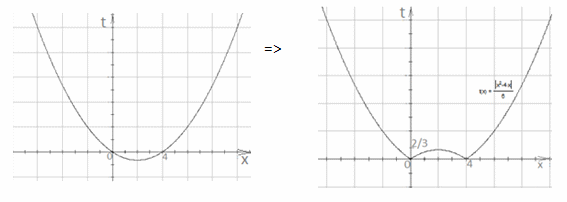 Проведем прямую t = k и найдем точки пересечения этой прямой с построенным графиком. В результате исследований получаем:Пример 8.При каком значении m функция
Проведем прямую t = k и найдем точки пересечения этой прямой с построенным графиком. В результате исследований получаем:Пример 8.При каком значении m функция 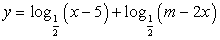 имеет минимум в точке с абсциссой, равной 6,5?Решение:Найдем область определения функции:
имеет минимум в точке с абсциссой, равной 6,5?Решение:Найдем область определения функции: 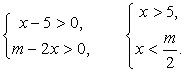 Значит,
Значит, 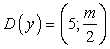 .Тогда функцию можно записать в следующем виде:
.Тогда функцию можно записать в следующем виде: 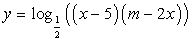 , т.е.
, т.е. 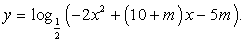 Ветви квадратичной функции направлены вниз, значит, она имеет максимум в точке х0, являющейся абсциссой вершины параболы. Точка максимума квадратичной функции совпадает с точкой минимума функции в силу того, что функция вида монотонно убывает при t > 0.Найдем абсциссу вершины квадратичной функции: х0 = (10+m)/4. По условию минимум должен быть в точке с абсциссой, равной 6,5: 6,5 = (10+m)/4.Отсюда m = 16 .Ответ: 16.Пример 9.При каком значении параметра касательная, проведенная к графику функции
Ветви квадратичной функции направлены вниз, значит, она имеет максимум в точке х0, являющейся абсциссой вершины параболы. Точка максимума квадратичной функции совпадает с точкой минимума функции в силу того, что функция вида монотонно убывает при t > 0.Найдем абсциссу вершины квадратичной функции: х0 = (10+m)/4. По условию минимум должен быть в точке с абсциссой, равной 6,5: 6,5 = (10+m)/4.Отсюда m = 16 .Ответ: 16.Пример 9.При каком значении параметра касательная, проведенная к графику функции 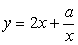 в точке с абсциссой x0 = 1, параллельна прямой y = -5x + 4?Решение:Если касательная, проведенная к графику функции в точке параллельна некоторой прямой, то производная функции в точке касания равна угловому коэффициенту прямой. Найдем производную функции в точке с абсциссой x0 = 1: у' = 2 – a/х2 ; у' = -5; 2 – a/х2 = -5; a = 7.Ответ: 7.Пример 10.При каких значениях параметра a функция
в точке с абсциссой x0 = 1, параллельна прямой y = -5x + 4?Решение:Если касательная, проведенная к графику функции в точке параллельна некоторой прямой, то производная функции в точке касания равна угловому коэффициенту прямой. Найдем производную функции в точке с абсциссой x0 = 1: у' = 2 – a/х2 ; у' = -5; 2 – a/х2 = -5; a = 7.Ответ: 7.Пример 10.При каких значениях параметра a функция 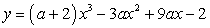 монотонно убывает на всей числовой оси?Решение:Функция убывает на всей числовой прямой, если ее производная неположительная на всей числовой прямой.Найдем производную функции, составим соответствующее неравенство и решим его:
монотонно убывает на всей числовой оси?Решение:Функция убывает на всей числовой прямой, если ее производная неположительная на всей числовой прямой.Найдем производную функции, составим соответствующее неравенство и решим его: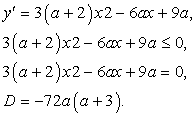 Чтобы неравенство выполнялось при всех действительных х, необходимо выполнение двух условий:
Чтобы неравенство выполнялось при всех действительных х, необходимо выполнение двух условий: 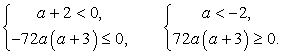
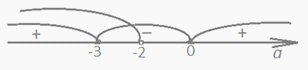 Ответ:
Ответ: 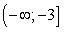 .Пример 11.При каком наибольшем значении a функция
.Пример 11.При каком наибольшем значении a функция 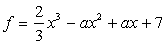 возрастает на всей числовой прямой?Решение:Производная функции неотрицательна на всей числовой прямой. Составим соответствующее неравенство и решим его:
возрастает на всей числовой прямой?Решение:Производная функции неотрицательна на всей числовой прямой. Составим соответствующее неравенство и решим его: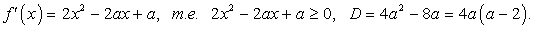 Чтобы неравенство выполнялось при всех действительных х, необходимо чтобы (так как коэффициент при х2 положителен). Неравенство верно при
Чтобы неравенство выполнялось при всех действительных х, необходимо чтобы (так как коэффициент при х2 положителен). Неравенство верно при 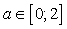 . Выберем наибольшее.Ответ: 2.Пример 12.При каких значениях параметров а и b все решения неравенства
. Выберем наибольшее.Ответ: 2.Пример 12.При каких значениях параметров а и b все решения неравенства 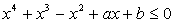 образуют отрезок [-2; 1] ?Решение:Для выполнения условия задачи необходимо, чтобы числа -2 и 1 были корнями уравнения
образуют отрезок [-2; 1] ?Решение:Для выполнения условия задачи необходимо, чтобы числа -2 и 1 были корнями уравнения 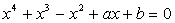 . Подставив эти значения в уравнение, получим систему уравнений для определения а и b:
. Подставив эти значения в уравнение, получим систему уравнений для определения а и b: 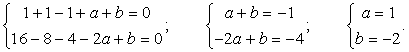 Убедимся, что уравнение x4 + x3 – x2 + x – 2 = 0 не имеет других корней. Разложим его левую часть на множители: (х - 1)(х + 2)(х2 + 1) = 0. Видим, что последний множитель не обращается в 0, поэтому других корней уравнение не имеет.Вернемся к решению неравенства. Запишем его в виде:
Убедимся, что уравнение x4 + x3 – x2 + x – 2 = 0 не имеет других корней. Разложим его левую часть на множители: (х - 1)(х + 2)(х2 + 1) = 0. Видим, что последний множитель не обращается в 0, поэтому других корней уравнение не имеет.Вернемся к решению неравенства. Запишем его в виде: 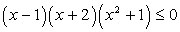 . Метод интервалов дает решение [-2; 1], то есть условие задачи выполнено.Ответ: а = 1, b = -2.Пример 13.При каких значениях параметра a число является периодом функции
. Метод интервалов дает решение [-2; 1], то есть условие задачи выполнено.Ответ: а = 1, b = -2.Пример 13.При каких значениях параметра a число является периодом функции 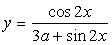 ?Решение:Для того чтобы число являлось периодом указанной функции, необходимо выполнение равенства
?Решение:Для того чтобы число являлось периодом указанной функции, необходимо выполнение равенства 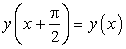 при всех допустимых х, по определению периодической функции. Составим соответствующее уравнение и решим его:
при всех допустимых х, по определению периодической функции. Составим соответствующее уравнение и решим его: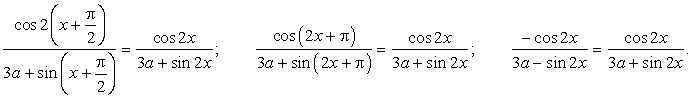 Данное равенство справедливо лишь при a = 0.Ответ: 0.Пример 14.Найти все значения а, при которых выражение
Данное равенство справедливо лишь при a = 0.Ответ: 0.Пример 14.Найти все значения а, при которых выражение 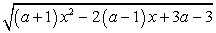 имеет смысл при всех действительных числах.Решение:Данное задание можно переформулировать следующим образом: найти все значения а, при которых областью определения функции являются все действительные числа.Значит, для всех действительных чисел должно выполняться неравенство
имеет смысл при всех действительных числах.Решение:Данное задание можно переформулировать следующим образом: найти все значения а, при которых областью определения функции являются все действительные числа.Значит, для всех действительных чисел должно выполняться неравенство 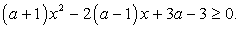 Сначала запишем уравнение
Сначала запишем уравнение 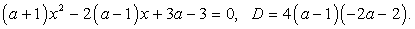 Чтобы неравенство было справедливо при всех действительных х, то
Чтобы неравенство было справедливо при всех действительных х, то 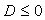 .Составим неравенство и решим его:
.Составим неравенство и решим его: 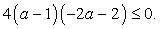 .Неравенство справедливо при всех а, таких что
.Неравенство справедливо при всех а, таких что 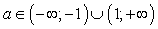 Выражение имеет смысл при всех действительных числах при таких а, что
Выражение имеет смысл при всех действительных числах при таких а, что 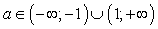 Ответ:
Ответ: 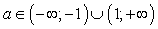 .Список используемой литературы Видеолекция «Задания с параметром»:
.Список используемой литературы Видеолекция «Задания с параметром»: 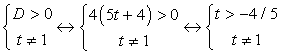 ,
,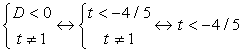 ,
,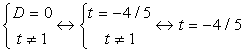
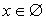 ; если
; если 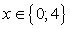 ;
;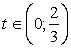 , то
, то 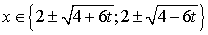 ;
; ;
;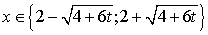 .
.
