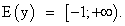Возрастание, убывание, экстремум функций (без нахождения производной)
и убывание функции, в которых не надо вычислять производные.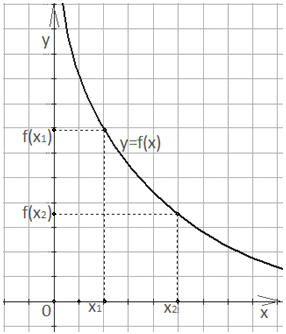
Функцию у = f(x) называют убывающей на промежутке, если для любых x1 и x2 принадлежавших этому промежутку, из условия x2 > x1 следует, что f(x2) < f(x1).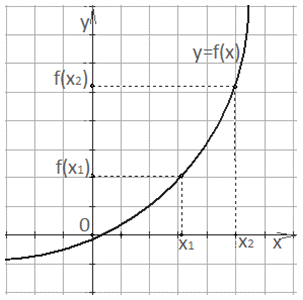
Функцию у = f(x) называют возрастающей на промежутке, если для любых x1 и x2, принадлежавших этому промежутку, из условия x2 > x1 следует, что f(x2) > f(x1).Т.е. положительному приращению аргумента ∆х = x2 — x1 > 0 соответствует положительное приращение функции ∆f = f(x2) — f(x1) > 0. Значит, 
Отсюда 
Аналогично доказывается и для убывающей функции. Итак, получили правило:Если на промежутке производная функции положительна, то функция возрастает.Если на промежутке производная функции отрицательна, то функция убывает.Точки области определения функции, в которых производная равна нулю, называются стационарными точками.Точки, в которых производная равна нулю или не существует, называются критическими точками.Если при переходе через критическую точку х0 ϵ D(f), производная функции меняет знак с «+» на «-», то х0 — точка локального максимума функции.Если при переходе через критическую точку х0 ϵ D(f), производная функции меняет знак с «-» на «+», то х0 — точка локального минимума функции.Пример 1.Определить по графику промежутки возрастания функции.
РешениеЕсли функция возрастает, то при движении по графику слева направо ординаты увеличиваются. Следовательно, функция возрастает на отрезках [-6; 0] U [6; 9].Ответ: [-6; 0] U [6; 9].Пример 2.Определить по графику промежутки убывания функции.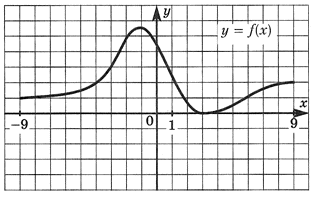
РешениеЕсли функция убывает, то при движении по графику слева направо ординаты уменьшаются. Следовательно, функция убывает на отрезке [-1; 2].Ответ: [-1; 2].Пример 3.Укажите график возрастающей функции.
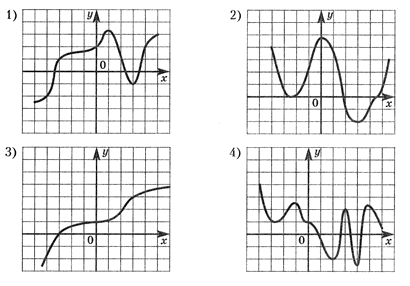Ответ: 3.Пример 4.Укажите график убывающей функции.
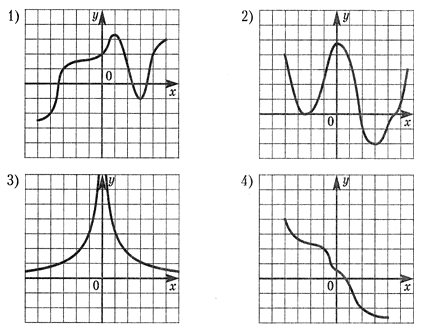Ответ: 4.Пример 5.Указать интервалы возрастания функций, графики которых представлены на рисунках:
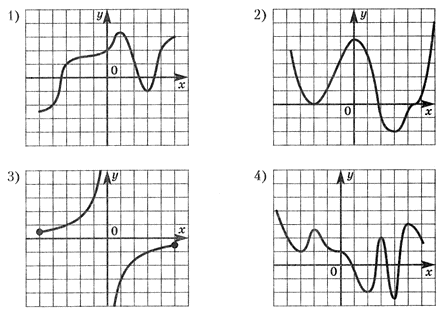Ответ:- 1) [-5; 1] U [3; 5];2) [-3; 0]U[3; 6];3) [-5; 0) U (0; 5];4) [-3; -2] U [2; 3] U [4; 5].
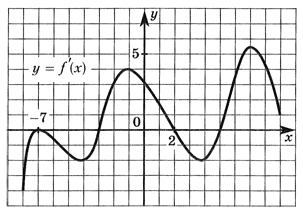
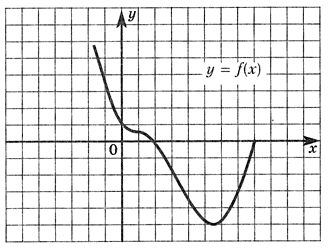РешениеЗаметим, что с = f(0), следовательно, с > 0.Также заметим, что b = f'(0), и, следовательно, b < 0, так как на интервале, содержащем точку 0, функция убывает.Ответ: с > 0, b < 0.Пример 7.Определить по графику производной функции у = f'(x) точку максимума.
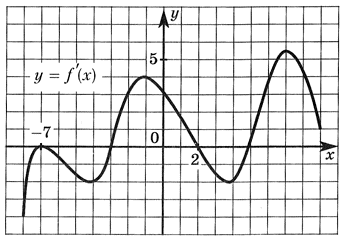РешениеЕсли при переходе через критическую точку х0 ϵ D(f) производная функции меняет знак с «+» на «-», то х0 — точка локального максимума функции.Критическими точками функции являются точки -7, -3, 2, 5. Производная меняет знак с «+» на «-» в точке х0 = 2.Ответ: 2.Пример 8.Указать интервалы убывания функции, если задан график ее производной.
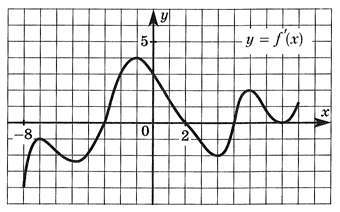РешениеЕсли непрерывная функция убывает на множестве, то ее производная не больше нуля (график ниже оси ОХ). Поэтому, функция убывает на [-8; -3] U [2; 5].Ответ: [-8; -3] U [2; 5].Пример 9.Определить по графику функции у = kx + b знаки коэффициентов k и b.
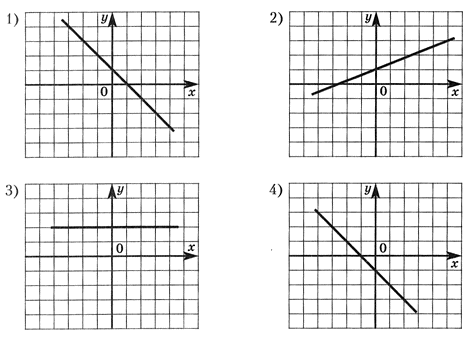Ответы:- 1) k < 0, b > 0;2) k > 0, b > 0;3) k = 0, b > 0;4) k < 0, b < 0.
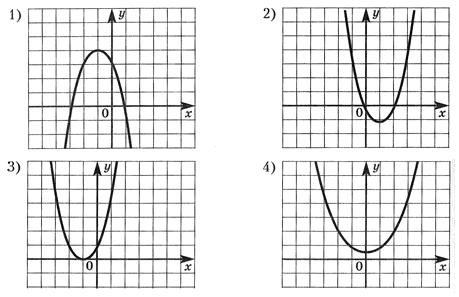Решение1) Ветви параболы вниз, значит a < 0. Коэффициент с найдем как у(0) = с, очевидно, c > 0. Если парабола пересекает ось ОХ в двух точках, то дискриминант положительный. Коэффициент b найдем из формулы для, заметим, отрицательной абсциссы вершины параболы: 
Аналогично рассуждают и в 2) — 4).Ответы:- 1) a < 0, b < 0, c > 0, D > 0;2) a > 0, b < 0, c = 0, D > 0;3) a > 0, b > 0, c > 0, D = 0;4) a > 0, b = 0, c > 0, D < 0.
РешениеЕсли при переходе через критическую точку х0 ϵ D(f) производная функции меняет знак с «-» на «+», то х0 — точка локального минимума функции.Критическими точками функции являются точки -7, -3, 2, 5. Производная меняет знак с «-» на «+» в точках -3 и 5. Значит ответ -3 + 5 = 2.Ответ: 2.Пример 12.Определить точку максимума функции у = f (x), если дан график ее производной. Если таких точек несколько, то найти их произведение.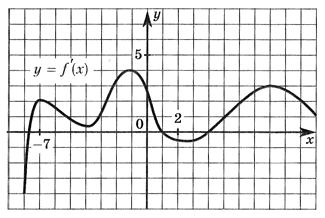
РешениеЕсли при переходе через критическую точку х0 ϵ D(f) производная функции меняет знак с «+» на «-», то х0 — точка локального максимума функции.Критическими точками функции являются точки -7,4; 1; 4. Производная меняет знак с «+» на «-» в точке х0 = 1.Ответ: 1.Пример 13.На рисунке изображен график производной функции f (x), определенной на интервале (-3; 8). Найдите промежутки убывания функции f (x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
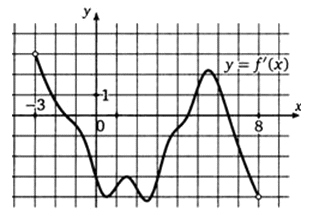РешениеФункция убывает на тех промежутках, на которых график производной находится ниже оси ОХ. Это примерно такие промежутки:(-1,5; 4,5), (6,5; 8). Количество целых точек, входящих в эти промежутки, — 7. Найдем сумму этих точек: -1 + 0 + 1 + 2 + 3 + 4 + 7 = 16.Ответ: 16.Пример 14.На рисунке изображен график производной функции f (x), определенной на интервале (-7; 5). Найдите точку экстремума функции f (x), принадлежащей отрезку [-6; 4].
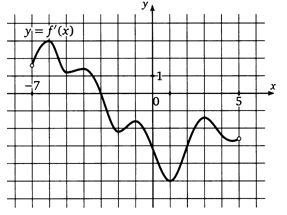РешениеПроизводная равна нулю в точке х = -3. В этой точке производная меняет знак с «+» на «-», значит х = -3 — точка локального максимума.Ответ: -3.Пример 15.На рисунке изображен график производной функции f (x), определенной на интервале (-3; 8). Найдите количество точек максимума функции f (x), принадлежащих отрезку [-2; 7].
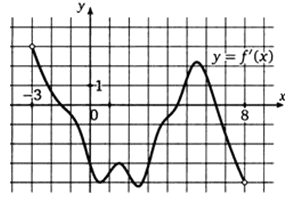РешениеГрафик функции в трех точках пересекает ось ОХ. И только в двух из них производная меняет знак с «+» на «-».Ответ: 2.Пример 16.На рисунке изображен график производной функции f (x), определенной на интервале (-11; 3). Найдите промежутки возрастания функции f (x). В ответе укажите длину наибольшего из них.
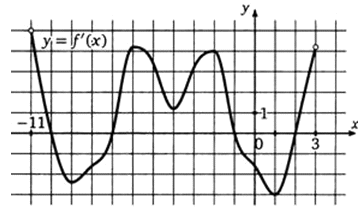РешениеФункция возрастает на тех промежутках, на которых график производной расположен выше оси ОХ. Это промежутки: (-11; -10), (-7; -1), (2; 3). Длина наибольшего из них равна -1 — (-7) = 6.Ответ: 6.Пример 17.Найти множество значений функции:
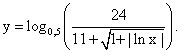Схема решения- Поочередно найти множества значений функции
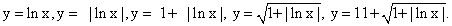
- Найти множество значений дроби
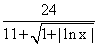
- Найти искомое множество решений.
- Множество значений логарифмической функции — вся числовая прямая, т.е. E(lnx) = R. Поэтому
- По свойствам неравенств
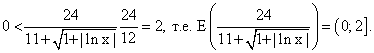
- Так как
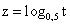— убывающая и непрерывная функция, то
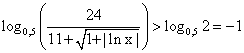и 
