Комбинированные задачи
треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны.Все три медианы треугольника пересекаются в одной точке. Эта точка пересечения называется центроидром или центром тяжести треугольника.Свойства медиан треугольникаМедиана разбивает треугольник на два треугольника одинаковой площади.Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2 : 1, считая от вершины. Эта точка называется центром тяжести треугольника.Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.Перпендикуляр, опущенный из вершины треугольника на противоположную сторону или ее продолжение, называется высотой треугольника.Свойства высот треугольникаВ прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.Если треугольник остроугольный, то все основания высот принадлежат сторонам треугольника, а у тупоугольного треугольника две высоты попадают на продолжение сторон.Три высоты в остроугольном треугольнике пересекаются в одной точке и эту точку называют ортоцентром треугольника.Биссектрисой треугольника, проведенной из данной вершины, называют отрезок, соединяющий эту вершину с точкой на противоположной стороне и делящий угол при данной вершине пополам.Свойства биссектрис треугольникаБиссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла (рис. 1 
).Биссектриса внутреннего угла треугольника делит противоположную сторону на отрезки, пропорциональные прилегающим сторонам.Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.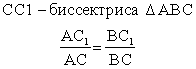
Длина биссектрисы
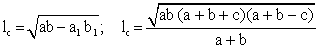В равнобедренном треугольнике биссектриса, медиана и высота, проведенные к основанию, совпадают. Верно и обратное: если биссектриса, медиана и высота, проведенные из одной вершины, совпадают, то треугольник равнобедренный.Если треугольник разносторонний, то для любой его вершины биссектриса, проведенная из нее, лежит между медианой и высотой, проведенными из той же вершины.Серединные перпендикуляры к сторонам треугольника также пересекаются в одной точке, которая совпадает с центром описанной окружности.Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.Свойства серединных перпендикуляров треугольникаКаждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.Свойство средней линии треугольникаСредняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.Решение косоугольных треугольниковТеорема синусов
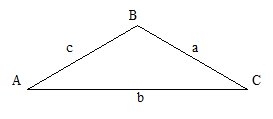
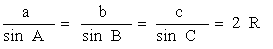Теорема косинусов
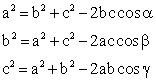Соотношения между сторонами и углами в прямоугольном треугольнике: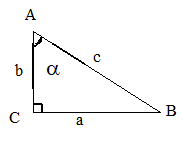
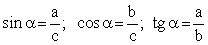Длина медианы треугольника выражается формулой:
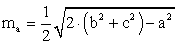.Длина стороны треугольника через медианы выражается формулой:
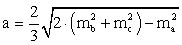.Длина биссектрисы треугольника выражается формулой:
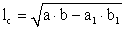.Длина высоты:
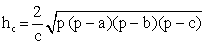Прямоугольный треугольник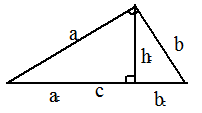
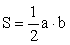
a, b — катеты; c — гипотенуза; ac, bc — проекции катетов на гипотенузу:Теорема Пифагора
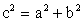
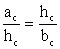
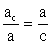
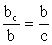Решение прямоугольных треугольников
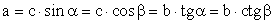.Пример 1.В треугольнике ABC AB = BC, AC = 5, cos C = 0,8. Найдите высоту CH.
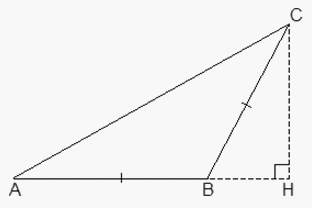РешениеОбозначим искомую высоту CH = x. Перед нами равнобедренный треугольник ABC, в котором AB = BC. Следовательно, согласно свойствам равнобедренного треугольника, имеем: 
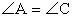и cos A = cos C = 0,8.Рассмотрим треугольник ACH. Он прямоугольный (
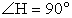), причем AC = 5 и cos A = 0,8. По определению, 
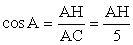. Получаем пропорцию:
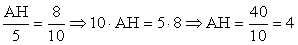.Осталось воспользоваться теоремой Пифагора для треугольника ACH:
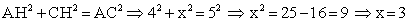.Ответ: 3.Пример 2.В прямоугольном треугольнике ABC 
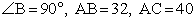. Найти синус угла CAD.
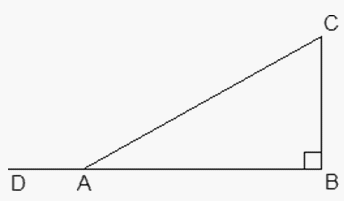РешениеПоскольку нам известна гипотенуза AC = 40 и катет AB = 32, можно найти косинус угла A: 
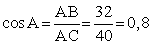.Зная косинус, можно найти синус через основное тригонометрическое тождество:
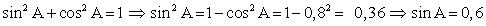.При нахождении синуса вновь был использован тот факт, что тригонометрические функции острого угла положительны. Осталось заметить, что углы BAC и CAD смежные. Имеем:
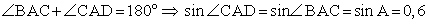.Ответ: 0,6Пример 3.В треугольнике ABC AC = BC = 5, AB = 8, CH — высота. Найдите tg A.
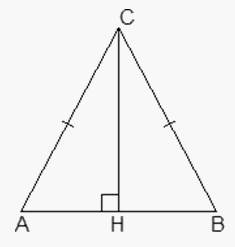РешениеТреугольник ABC — равнобедренный, CH — высота, поэтому заметим, что AH = BH = 0,5 • AB = 0,5 • 8 = 4 — по свойствам равнобедренного треугольника.Теперь рассмотрим треугольник ACH: в нем 
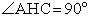. Можно выразить тангенс: 
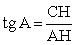. Но AH = 4, поэтому остается найти сторону CH, которую обозначим CH = x. По теореме Пифагора имеем:
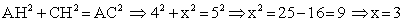.Теперь все готово, чтобы найти тангенс: 
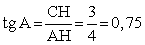.Ответ: 0,75Пример 4.В треугольнике ABC AC = BC, AB = 6, cos A = 3/5. Найти высоту AH.
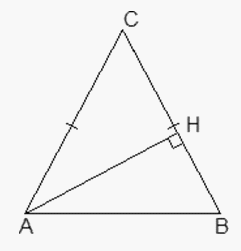РешениеОбозначим искомую высоту AH = x. Снова треугольник ABC — равнобедренный, поэтому заметим, что 
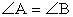, следовательно, 
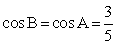.Рассмотрим треугольник ABH. По условию, он прямоугольный (
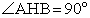), причем известна гипотенуза AB = 6 и 
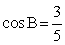. Но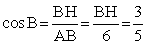 
. Получили пропорцию:
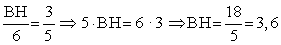.Теперь найдем AH = x по теореме Пифагора для треугольника ABH:
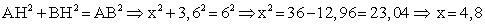Ответ: 4,8.Дополнительные соображенияБывают нестандартные задачи, где рассмотренные выше факты и схемы бесполезны. Увы, в таком случае нужен действительно индивидуальный подход. Подобные задачи любят давать на всевозможных «пробных» и «демонстрационных» экзаменах.Ниже приведены две реальные задачи, которые предлагались на пробном ЕГЭ в Москве. Справились с ними единицы, что свидетельствует о высокой сложности этих задач.Пример 5.В прямоугольном треугольнике ABC из угла C = 90° провели медиану и высоту. Известно, что 
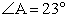. Найти 
.
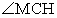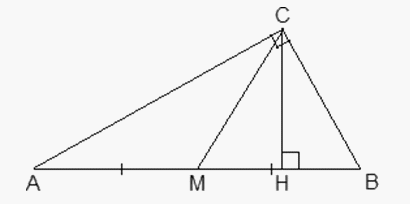РешениеЗаметим, что медиана CM проведена к гипотенузе AB, поэтому M — центр описанной окружности, т.е. AM = BM = CM = R, где R — радиус описанной окружности. Следовательно, треугольник ACM — равнобедренный, и 
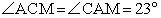.Теперь рассмотрим треугольники ABC и CBH. По условию, оба треугольника прямоугольные. Кроме того, 
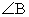— общий. Следовательно, треугольники ABC и CBH подобны по двум углам.В подобных треугольниках соответствующие элементы пропорциональны. В частности, 
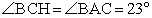.Наконец, рассмотрим 
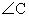. Он прямой, и, кроме того, 
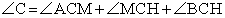. В этом равенстве 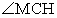— искомый, а 
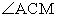и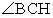 
известны и равны 23°. Имеем:
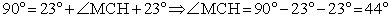.Ответ: 44°Пример 6.Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника.
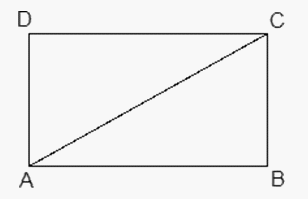РешениеОбозначим стороны прямоугольника: AB = x, BC = y. Выразим периметр: 
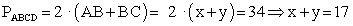.Аналогично выразим площадь: SABCD = AB • BC = x • y = 60.Теперь рассмотрим треугольник ABC. Он прямоугольный, поэтому запишем теорему Пифагора:
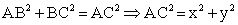.Заметим, что из формулы квадрата разности следует равенство:x2 + y2 = (x + y)2 - 2 • x • y = 172 - 2 • 60 = 289 - 120 = 169.Итак, AC2 = 169, откуда AC = 13.Ответ: 13. Видеолекция «Комбинированные задачи»: 
