Окружность, вписанная в треугольник. Окружность, описанная вокруг треугольника
(рис. 1
).Окружность, проходящая через все три вершины треугольника, называется его описанной окружностью (рис. 2
).Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны.Все три медианы треугольника пересекаются в одной точке. Эта точка пересечения называется центроидром или центром тяжести треугольника.Центроид делит каждую медиану в отношении 1 : 2, считая от основания медианы.Перпендикуляр, опущенный из вершины треугольника на противоположную сторону или ее продолжение, называется высотой треугольника.Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.Биссектрисой треугольника, проведенной из данной вершины, называют отрезок, соединяющий эту вершину с точкой на противоположной стороне и делящий угол при данной вершине пополам.Биссектрисы треугольника пересекаются в одной точке, и эта точка совпадает с центром вписанной окружности.В равнобедренном треугольнике биссектриса, медиана и высота, проведенные к основанию, совпадают. Верно и обратное: если биссектриса, медиана и высота, проведенные из одной вершины, совпадают, то треугольник равнобедренный.Если треугольник разносторонний, то для любой его вершины биссектриса, проведенная из нее, лежит между медианой и высотой, проведенными из той же вершины.Серединные перпендикуляры к сторонам треугольника также пересекаются в одной точке, которая совпадает с центром описанной окружности.Вне вписанной окружностью называется окружность, касающаяся одной стороны треугольника и продолжения двух других сторон.Середины трех сторон треугольника, основания трех его высот и середины трех отрезков, соединяющих его вершины с ортоцентром, лежат на одной окружности, называемой окружностью девяти точек.Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны этого треугольника.Свойства медиан треугольникаМедиана разбивает треугольник на два треугольника одинаковой площади.Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2 : 1, считая от вершины. Эта точка называется центром тяжести треугольника.Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам.Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.Свойства биссектрис треугольникаБиссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.Биссектриса внутреннего угла треугольника делит противоположную сторону на отрезки, пропорциональные прилегающим сторонам.Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.Свойства высот треугольникаВ прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.Если треугольник остроугольный, то все основания высот принадлежат сторонам треугольника, а у тупоугольного треугольника две высоты попадают на продолжение сторон.Три высоты в остроугольном треугольнике пересекаются в одной точке и эту точку называют ортоцентром треугольника.Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.Свойства серединных перпендикуляров треугольникаКаждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.Свойство средней линии треугольникаСредняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.В произвольном треугольнике: a, b, c — стороны; α, β, γ — противолежащие им углы; p — полупериметр; R — радиус описанной окружности; r — радиус вписанной окружности; S — площадь; ha — высота, проведенная к стороне a: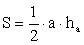
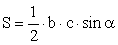
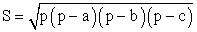
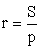
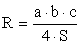Если d — расстояние между центрами вписанной и описанной окружностей, а их радиусы равны r и R соответственно, то d2 = R2 — 2Rr.Соотношения между сторонами и углами в прямоугольном треугольнике: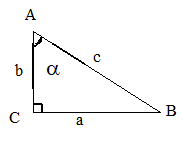
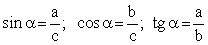Длина медианы треугольника выражается формулой:
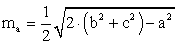.Длина стороны треугольника через медианы выражается формулой:
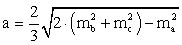.Длина биссектрисы треугольника выражается формулой:
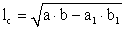.Длина высоты:
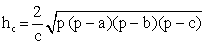Прямоугольный треугольник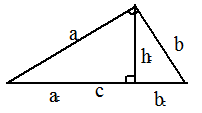
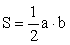
Теорема Пифагора
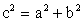
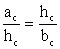
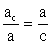
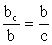Решение прямоугольных треугольников
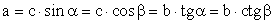.Равносторонний треугольник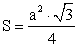
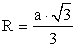Свойства биссектрисы внутреннего угла
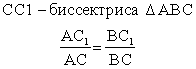Длина биссектрисы
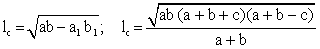Окружность, круг(r — радиус; C — длина окружности; S — площадь круга):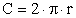
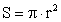Сектор:(l — длина дуги, ограничивающей сектор; α° — градусная мера центрального угла; φ — радианная мера центрального угла):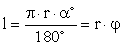
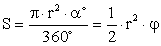Теоремы, относящиеся к понятию «окружность»:- радиус, проведенный в точку касания, перпендикулярен касательной;
- диаметр, проходящий через середину хорды, перпендикулярен ей;
- квадрат длины касательной равен произведению длины секущей на ее внешнюю часть;
- центральный угол измеряется градусной мерой дуги, на которую он опирается;
- вписанный угол измеряется половиной дуги, на которую он опирается, или дополняет его половину до 180°;
- касательные, проведенные к окружности из одной точки, равны;
- произведение секущей на ее внешнюю часть — величина постоянная.
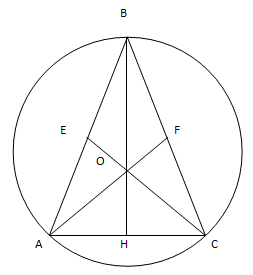РешениеДано: ∆ ABC — равнобедренный, AC — основание, 
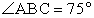,площадь ∆ BOC равна 16.Найти радиус описанной окружности.Проведем медианы AF, CE, BH.∆ ABC — равнобедренный, BH — медиана, следовательно, BH — высота, а значит ∆ HBC — прямоугольный.
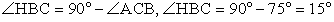BO = OC = R, следовательно, ∆ BOC — равнобедренный, значит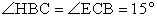 
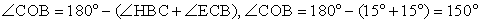
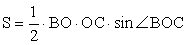(теорема о площади треугольника)
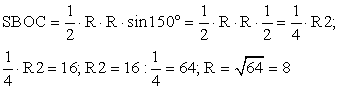Ответ: R = 8.Пример 2.Треугольник BMP с углом B, равным 45°, вписан в окружность радиуса 6. Найдите длину медианы BK, если BKпересекает окружность в точке C и CK = 3.
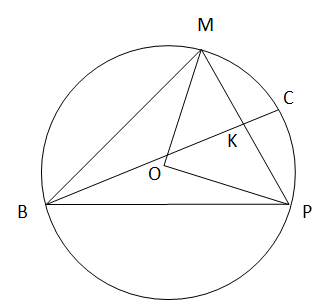Решение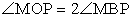
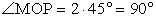, следовательно, ∆ MOP — прямоугольный.MP2 = OM2 + OP2MP2 = 62 + 62 = 36 + 36 = 36 ∙ 2
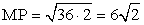MK = KP = 0,5 ∙ MP
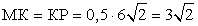MK ∙ KP = BK ∙ KC
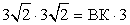BK ∙ 3 = 9 ∙ 2BK ∙ 3 = 18BK = 6Ответ: BK = 6.Пример 3.Остроугольный равнобедренный треугольник BCD с основанием CD, равным 16, вписан в окружность с центром O и радиусом 10. Найдите площадь треугольника BOC.
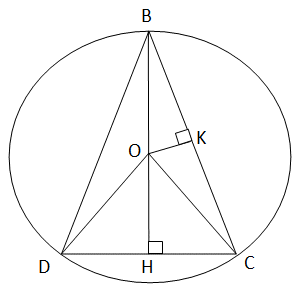Решение∆ BCD — равнобедренный, CD = 16, следовательно, DH = HC = 8∆ DOH — прямоугольныйПо теореме Пифагора:OH2 = 102 — 82OH2 = 100 — 64 = 36OH = 6BH = BO + OH = 10 + 6 =16По теореме Пифагора:BC2 = 162 + 82 = 256 + 64 = 320
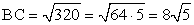∆ KBO ~ ∆ HBC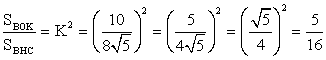
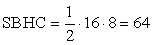
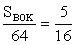SBOK = 20SBOC = 2 ∙ SBOK = 2 ∙ 20 = 40Ответ: SBOC = 40.Пример 4.Радиус окружности, вписанной в прямоугольный треугольник, равен 2 м, а радиус описанной окружности равен 5 м. Найдите больший катет треугольника.
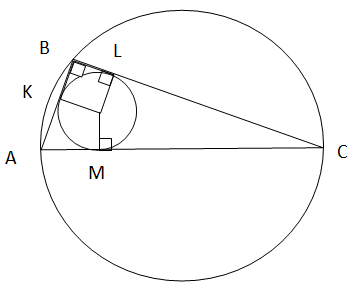РешениеAC = 2r = 10 мПусть AM = AK = x, MC = CL = yПо теореме Пифагора:x + y = 10(x + 2)2 + (y + 2)2 = (x + y)2y = 10 — x(x + 2)2 + (10 — x + 2)2 = (x + 10 — x)2(x + 2)2 + (12 — x)2 = 100x2 + 4x + 4 + 144 — 24x + x2 = 1002x2 — 20x + 148 = 1002x2 — 20x + 48 = 0x2 — 10x + 24 = 0x1 = 6, x2 = 4y = 10 — xx = 6 x = 4y = 4 y = 6Так как нужно найти больший катет, то берем y = 6.BC = 2 + 6 = 8 мОтвет: BС = 8 м.Пример 5.Окружность, вписанная в равнобедренный треугольник, касается его боковых сторон в точках K и A. Точка K делит сторону этого треугольника на отрезки 15 и 10, считая от основания. Найдите длину отрезка KA.
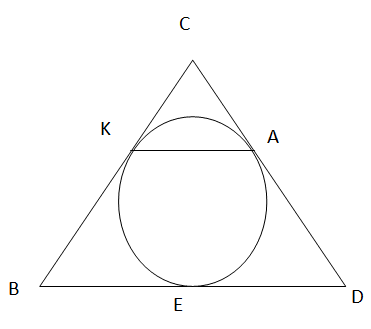Дано: ∆ BCD — равнобедренный, K ϵ BC, A ϵ DC, BK = 15, KC = 10Найти: KA.CD = CB = BK + KC, CD = CB = 15 + 10 = 25CK = CA = 10 (отрезки касательных, проведенные из одной точки), CB = CD, следовательно AD = CD — CA, AD = 25 — 10 = 15BE = BK = 15, DE = DA = 15 (отрезки касательных, проведенные из одной точки), следовательно BD = 15 + 15 = 30∆ CKA ~ ∆ CBD (
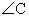— общий, CK : CB = CA : CD), следовательно KA : BD = CA : CD, KA : 30 = 10 : 25, KA = 10 ∙ 30 : 25 = 12Ответ: KA = 12. Видеолекция «Тест. Окружность, вписанная в треугольник. Окружность, описанная вокруг треугольника»: 
