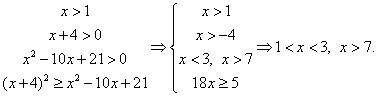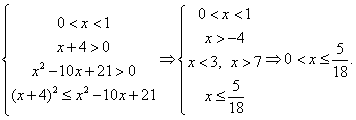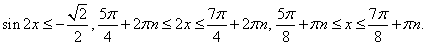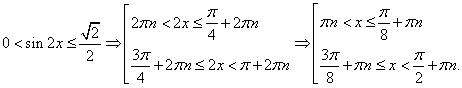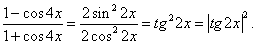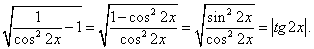Комбинированные неравенства
 применяют так называемый метод интервалов
применяют так называемый метод интервалов . Практика вступительных испытаний по математике показывает, что абитуриенты не всегда правильно используют этот метод, понимают его сущность и специфику. В значительной степени это связано с тем, что в учебной литературе встречаются различные подходы к изложению метода интервалов, далеко не всегда удачные. Имеет место путаница с терминами, «странные синтезы» сразу нескольких подходов. Но алгоритм метода интервалов
. Практика вступительных испытаний по математике показывает, что абитуриенты не всегда правильно используют этот метод, понимают его сущность и специфику. В значительной степени это связано с тем, что в учебной литературе встречаются различные подходы к изложению метода интервалов, далеко не всегда удачные. Имеет место путаница с терминами, «странные синтезы» сразу нескольких подходов. Но алгоритм метода интервалов требует строгости и четкости.Будем понимать метод интервалов как метод, применяемый для решения рациональных неравенств строго определенного вида:
требует строгости и четкости.Будем понимать метод интервалов как метод, применяемый для решения рациональных неравенств строго определенного вида: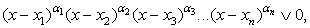 где x1, x2, x3, …, xn ϵ R;α1, α2, α3,…, αn ϵ N и V — любой из знаков неравенства >, <, ≥, ≤.Если данное неравенства не соответствует указанному виду, то его необходимо привести к этому виду теми или иными равносильными преобразованиями и лишь затем применять метод интервалов. Назовем указанный вид неравенства стандартным для решения методом интервалов.Введем еще два термина. Пусть
где x1, x2, x3, …, xn ϵ R;α1, α2, α3,…, αn ϵ N и V — любой из знаков неравенства >, <, ≥, ≤.Если данное неравенства не соответствует указанному виду, то его необходимо привести к этому виду теми или иными равносильными преобразованиями и лишь затем применять метод интервалов. Назовем указанный вид неравенства стандартным для решения методом интервалов.Введем еще два термина. Пусть 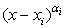 — множитель, входящий в неравенство, стандартное для решения методом интервалов. Если показатель степени αi — нечетное число, то точку х = xi будем называть простой. Если показатель степени αi — четное число, то точку х = xi будем называть двойной.Теперь сформулируем алгоритм метода интервалов.Пусть дано неравенство вида, стандартного для решения методом интервалов. Для его решения:
— множитель, входящий в неравенство, стандартное для решения методом интервалов. Если показатель степени αi — нечетное число, то точку х = xi будем называть простой. Если показатель степени αi — четное число, то точку х = xi будем называть двойной.Теперь сформулируем алгоритм метода интервалов.Пусть дано неравенство вида, стандартного для решения методом интервалов. Для его решения:- 1) отметим на числовой прямой точки, соответствующие числам x1, x2, x3,…, xn, разбив тем самым всю числовую прямую на промежутки (интервалы); причем если знак неравенства строгий, то точки отмечаются выколотыми, если знак неравенства нестрогий, то точки отмечаются сплошными;2) на каждом из полученных промежутков выражение
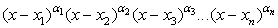 будет сохранять свой знак постоянным; расставим эти знаки пользуясь правилом чередования знаков:
будет сохранять свой знак постоянным; расставим эти знаки пользуясь правилом чередования знаков:- а) в крайнем правом интервале всегда знак «плюс»;б) при переходе через простую точку знак меняется на противоположный;в) при переходе через двойную точку знак сохраняется;
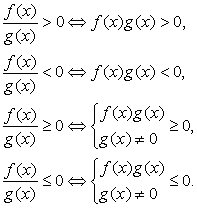 Подведем итог. Для применения метода интервалов нужно преобразовать неравенство так, чтобы в правой его части стоял 0, а левая была произведением нескольких множителей или дробью, числитель и знаменатель которой разложены на множители. Затем находятся корни каждого множителя (то есть от решения неравенства вы переходите к решению уравнений), и среди них выделяются такие, в которых ни один из имеющихся множителей не меняет знак или меняет знак четное количество множителей. В дальнейшем такие корни, если они найдутся, мы будем называть кратными
Подведем итог. Для применения метода интервалов нужно преобразовать неравенство так, чтобы в правой его части стоял 0, а левая была произведением нескольких множителей или дробью, числитель и знаменатель которой разложены на множители. Затем находятся корни каждого множителя (то есть от решения неравенства вы переходите к решению уравнений), и среди них выделяются такие, в которых ни один из имеющихся множителей не меняет знак или меняет знак четное количество множителей. В дальнейшем такие корни, если они найдутся, мы будем называть кратными (хотя это не совсем точно). Для окончательного решения неравенства остается нанести найденные корни на числовую прямую, найти знак левой части неравенства только на одном интервале, ограниченном полученными точками, и расставить знаки на остальных интервалах, меняя их при переходе через простой корень и не меняя при переходе через кратный.Пример 1.Решим неравенство:
(хотя это не совсем точно). Для окончательного решения неравенства остается нанести найденные корни на числовую прямую, найти знак левой части неравенства только на одном интервале, ограниченном полученными точками, и расставить знаки на остальных интервалах, меняя их при переходе через простой корень и не меняя при переходе через кратный.Пример 1.Решим неравенство: 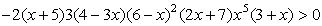 РешениеПриведем данное неравенство к стандартному для решения методом интервалов виду:
РешениеПриведем данное неравенство к стандартному для решения методом интервалов виду: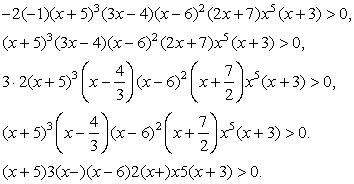 Построим разбиение числовой прямой на промежутки:
Построим разбиение числовой прямой на промежутки:  Заметим, что масштаб в данном случае соблюдать совсем необязательно, но отдельные принципиальные детали, относящиеся к уровню общей графической культуры, соблюдать, конечно, следует. Так, точка -3 должна быть изображена более удаленной от нуля, чем точка
Заметим, что масштаб в данном случае соблюдать совсем необязательно, но отдельные принципиальные детали, относящиеся к уровню общей графической культуры, соблюдать, конечно, следует. Так, точка -3 должна быть изображена более удаленной от нуля, чем точка 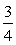 , а расстояние между точками
, а расстояние между точками 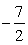 и -3 должно быть значительно меньше, чем расстояние между точками
и -3 должно быть значительно меньше, чем расстояние между точками 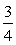 и 6 и т.д. Расставим знаки в промежутках, используя правило чередования:
и 6 и т.д. Расставим знаки в промежутках, используя правило чередования:  Из рисунка видно решение неравенства:
Из рисунка видно решение неравенства: 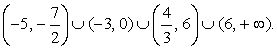 Ответ:
Ответ: 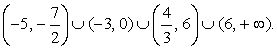 Пример 2.Решим неравенство:
Пример 2.Решим неравенство: 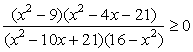 РешениеДанное неравенство равносильно системе:
РешениеДанное неравенство равносильно системе: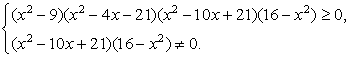 Приведем первое неравенство системы к виду, стандартному для решения методом интервалов:
Приведем первое неравенство системы к виду, стандартному для решения методом интервалов: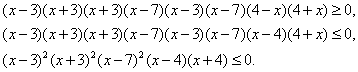 Построим разбиение числовой прямой на промежутки, учитывая второе неравенство системы, то есть, что х ≠ 3, х ≠ 7, х ≠ ± 4, и расставим знаки по правилу чередования:
Построим разбиение числовой прямой на промежутки, учитывая второе неравенство системы, то есть, что х ≠ 3, х ≠ 7, х ≠ ± 4, и расставим знаки по правилу чередования:  Решение неравенства:
Решение неравенства: 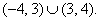 Ответ:
Ответ: 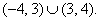 Решение показательных неравенств
Решение показательных неравенств сводится к решению простейших неравенств:
сводится к решению простейших неравенств: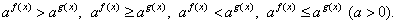 Важно помнить при этом, что при a > 1 можно перейти к неравенству, связывающему показатели степеней, знак которого совпадает со знаком исходного неравенства; при 0 < a < 1 показатели будут связаны неравенством противоположного знака. Т.е. если a > 1, то неравенства
Важно помнить при этом, что при a > 1 можно перейти к неравенству, связывающему показатели степеней, знак которого совпадает со знаком исходного неравенства; при 0 < a < 1 показатели будут связаны неравенством противоположного знака. Т.е. если a > 1, то неравенства 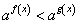 и
и 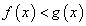 равносильны; если 0 < a < 1, то неравенства
равносильны; если 0 < a < 1, то неравенства 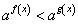 и
и 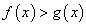 равносильны (это следует из того, что при a > 1 показательная функция возрастает, а при 0 < a < 1 убывает).Составим схемы равносильных преобразований для решения неравенств следующего вида:Пример 3.Решить неравенство:
равносильны (это следует из того, что при a > 1 показательная функция возрастает, а при 0 < a < 1 убывает).Составим схемы равносильных преобразований для решения неравенств следующего вида:Пример 3.Решить неравенство: 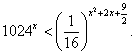 РешениеПредставим обе части неравенства как степени с основанием 2:
РешениеПредставим обе части неравенства как степени с основанием 2: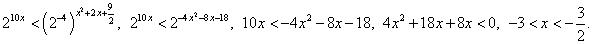 Ответ:
Ответ: 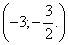 Пример 4.Решить неравенство:
Пример 4.Решить неравенство: 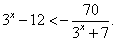 РешениеПосле замены t = 3x решим систему неравенств:
РешениеПосле замены t = 3x решим систему неравенств: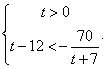 Поскольку знаменатель дроби в правой части второго неравенства при t > 0 положителен, можно умножить на него обе части неравенства, превратив его в квадратное:
Поскольку знаменатель дроби в правой части второго неравенства при t > 0 положителен, можно умножить на него обе части неравенства, превратив его в квадратное: 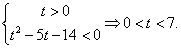 Сделаем обратную замену:
Сделаем обратную замену: 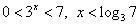 (левая часть неравенства верна при любом х).Ответ:
(левая часть неравенства верна при любом х).Ответ: 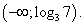 Пример 5.Решить неравенство:
Пример 5.Решить неравенство: 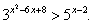 РешениеПерейдем к основанию 3:
РешениеПерейдем к основанию 3: 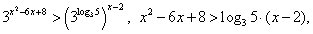
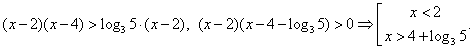 Ответ:
Ответ: 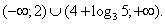 Пример 6.Решить неравенство:
Пример 6.Решить неравенство: 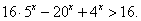 РешениеПеренесем все слагаемые в левую часть и разложим ее на множители:(16 — 4x)(5x — 1) > 0. Найдем корни левой части неравенства:
РешениеПеренесем все слагаемые в левую часть и разложим ее на множители:(16 — 4x)(5x — 1) > 0. Найдем корни левой части неравенства:- 1 случай. 16 — 4x = 0, х = 2;2 случай. 5x — 1 = 0, х = 0.
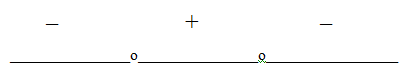 Итак, 0 < x < 2.Ответ: (0; 2).Пример 7.Решить неравенство:
Итак, 0 < x < 2.Ответ: (0; 2).Пример 7.Решить неравенство: 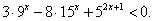 РешениеЗапишем неравенство в виде:
РешениеЗапишем неравенство в виде: 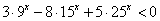 и разделим обе его части на 25x (при делении на положительное число знак неравенства не изменится):
и разделим обе его части на 25x (при делении на положительное число знак неравенства не изменится):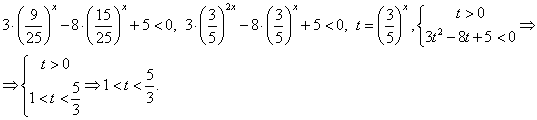 Сделаем обратную замену:
Сделаем обратную замену: 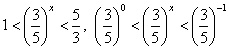 . Поскольку основание степени меньше 1, при переходе к показателям знак неравенства меняется: -1 < x < 0.Ответ: (-1; 0).Простейшее логарифмическое неравенство
. Поскольку основание степени меньше 1, при переходе к показателям знак неравенства меняется: -1 < x < 0.Ответ: (-1; 0).Простейшее логарифмическое неравенство 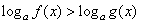 сводится к одной из двух систем неравенств:Пример 8.Решить неравенство:
сводится к одной из двух систем неравенств:Пример 8.Решить неравенство: 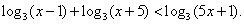 РешениеИспользуя свойства логарифмов, преобразуем левую часть:
РешениеИспользуя свойства логарифмов, преобразуем левую часть: 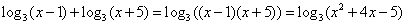 и решим систему неравенств:
и решим систему неравенств: 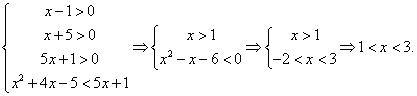 Обращаем ваше внимание на то, что положительным должно быть каждое логарифмируемое выражение, а не только их произведение.Ответ: (1; 3).Пример 9.Решить неравенство:
Обращаем ваше внимание на то, что положительным должно быть каждое логарифмируемое выражение, а не только их произведение.Ответ: (1; 3).Пример 9.Решить неравенство: 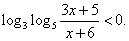 РешениеПоскольку 0 = log31, решаем неравенство
РешениеПоскольку 0 = log31, решаем неравенство 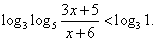 Оно равносильно системе:
Оно равносильно системе: 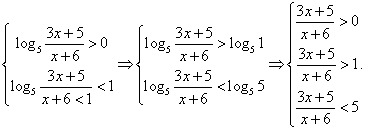 Заметим, что первое неравенство можно не решать, так как оно заведомо будет верным для всех решений второго неравенства. Тогда
Заметим, что первое неравенство можно не решать, так как оно заведомо будет верным для всех решений второго неравенства. Тогда 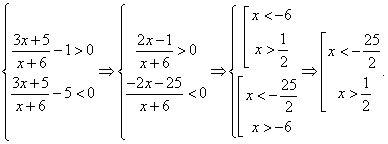 Ответ:
Ответ: 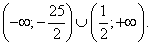 Комментарий. Если основание логарифма переменно и может принимать значения как меньшие, так и большие 1, нужно рассмотреть эти ситуации отдельно, так как в первом случае знак неравенства не меняется при переходе к аргументам, а во втором — меняется на обратный.Пример 10.Решить неравенство:
Комментарий. Если основание логарифма переменно и может принимать значения как меньшие, так и большие 1, нужно рассмотреть эти ситуации отдельно, так как в первом случае знак неравенства не меняется при переходе к аргументам, а во втором — меняется на обратный.Пример 10.Решить неравенство: 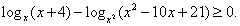 РешениеЗапишем неравенство в виде:
РешениеЗапишем неравенство в виде: 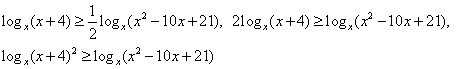 (учитываем, что x > 0, поэтому
(учитываем, что x > 0, поэтому 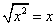 ).Ответ:
).Ответ: 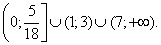 Основным методом решения иррациональных неравенств является метод возведения в степень
Основным методом решения иррациональных неравенств является метод возведения в степень . При этом решение таких неравенств сводится к решению рациональных неравенств или систем рациональных неравенств.Пример 11.Решить неравенство:
. При этом решение таких неравенств сводится к решению рациональных неравенств или систем рациональных неравенств.Пример 11.Решить неравенство: 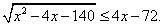 Вспомним свойства неравенств:
Вспомним свойства неравенств:- если обе части неравенства неотрицательны, то при возведении в квадрат знак неравенства не меняется;
- если отрицательны, то знак меняется на противоположный;
- если же левая и правая части имеют разные знаки, то возведение в квадрат является некорректной операцией.
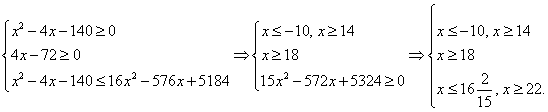 Пересечение решений можно записать в виде: х ≥ 22.Ответ: [22; +∞).Пример 12.Решить неравенство:
Пересечение решений можно записать в виде: х ≥ 22.Ответ: [22; +∞).Пример 12.Решить неравенство: 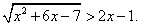 РешениеВ этом неравенстве, в отличие от предыдущего, правая часть может принимать значения разных знаков. Рассмотрим эти случаи отдельно.
РешениеВ этом неравенстве, в отличие от предыдущего, правая часть может принимать значения разных знаков. Рассмотрим эти случаи отдельно.- Случай 1. Если выполнены условия
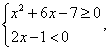 то неравенство будет верным: действительно, любое неотрицательное число больше любого отрицательного числа. Следовательно, все решения этой системы войдут в ответ. Решим полученную систему неравенств:
то неравенство будет верным: действительно, любое неотрицательное число больше любого отрицательного числа. Следовательно, все решения этой системы войдут в ответ. Решим полученную систему неравенств: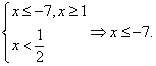 Случай 2. Вторая возможность — выполнение условий:
Случай 2. Вторая возможность — выполнение условий: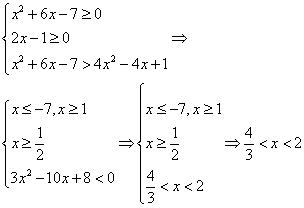 Ответ:
Ответ: 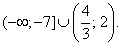
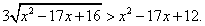 РешениеПусть
РешениеПусть 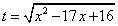 , тогда значения t определяются системой неравенств:
, тогда значения t определяются системой неравенств: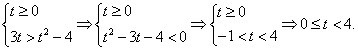 После обратной замены получим:
После обратной замены получим: 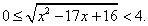 Поскольку левая и правая части этого двойного неравенства неотрицательны, мы можем возвести все три части в квадрат:
Поскольку левая и правая части этого двойного неравенства неотрицательны, мы можем возвести все три части в квадрат: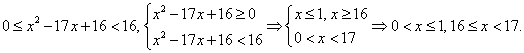 Ответ: (0; 1] U [16; 17).Пример 14.Решить неравенство:
Ответ: (0; 1] U [16; 17).Пример 14.Решить неравенство: 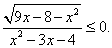 РешениеВо-первых,
РешениеВо-первых, 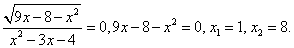 Во-вторых,
Во-вторых, 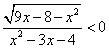 . Поскольку числитель дроби при всех допустимых значениях х неотрицателен, знаменатель должен принимать отрицательные значения, и неравенство сводится к системе:
. Поскольку числитель дроби при всех допустимых значениях х неотрицателен, знаменатель должен принимать отрицательные значения, и неравенство сводится к системе: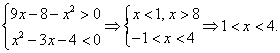 Объединяя найденные решения, получим окончательный ответ: 1 ≤ х < 4, x = 8.Еще раз обратите внимание на то, что если бы мы не рассматривали случай равенства отдельно, а решали систему неравенств
Объединяя найденные решения, получим окончательный ответ: 1 ≤ х < 4, x = 8.Еще раз обратите внимание на то, что если бы мы не рассматривали случай равенства отдельно, а решали систему неравенств 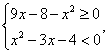 то потеряли бы решение х = 8.Ответ: [1; 4), x = 8.Комментарий. Если корень четной степени входит в нестрогое неравенство в качестве множителя, то, чтобы избежать потери решений, лучше рассмотреть отдельно случай равенства и строгого неравенства.Решением тригонометрического неравенства
то потеряли бы решение х = 8.Ответ: [1; 4), x = 8.Комментарий. Если корень четной степени входит в нестрогое неравенство в качестве множителя, то, чтобы избежать потери решений, лучше рассмотреть отдельно случай равенства и строгого неравенства.Решением тригонометрического неравенства обычно является набор промежутков, границы которых можно задать общей формулой с использованием целочисленного параметра. Для определения границ очень удобно применять тригонометрическую окружность
обычно является набор промежутков, границы которых можно задать общей формулой с использованием целочисленного параметра. Для определения границ очень удобно применять тригонометрическую окружность .Пример 15.Решить неравенство:
.Пример 15.Решить неравенство: 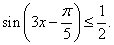 РешениеРешим сначала простейшее тригонометрическое неравенство
РешениеРешим сначала простейшее тригонометрическое неравенство 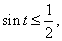 где
где 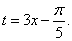
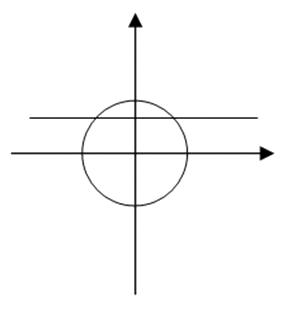 Прямая
Прямая 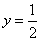 делит тригонометрическую окружность на две дуги. Решениям неравенства соответствуют точки на нижней дуге, ординаты которых не больше
делит тригонометрическую окружность на две дуги. Решениям неравенства соответствуют точки на нижней дуге, ординаты которых не больше 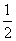 . Поэтому в пределах от
. Поэтому в пределах от 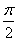 до
до 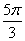 решение имеет вид:
решение имеет вид: 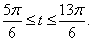 Границы следующего промежутка решений можно получить отсюда, изменив каждую границу на 2πn:
Границы следующего промежутка решений можно получить отсюда, изменив каждую границу на 2πn: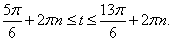 Сделав обратную замену, получим двойное неравенство для х:
Сделав обратную замену, получим двойное неравенство для х: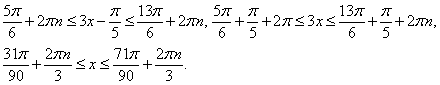 Ответ:
Ответ: 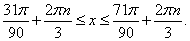 Пример 16.Решить неравенство: | tg x | ≥ 1.Решение
Пример 16.Решить неравенство: | tg x | ≥ 1.Решение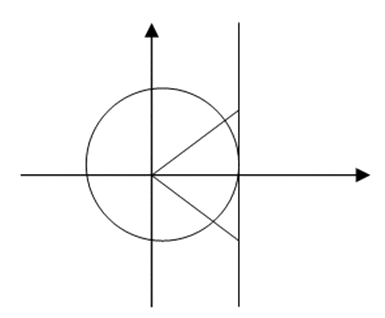 Наименьший положительный период тангенса равен π, поэтому достаточно найти решение неравенства на интервале
Наименьший положительный период тангенса равен π, поэтому достаточно найти решение неравенства на интервале 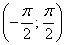 , а затем прибавить к границам πn. Раскрыв модуль, превратим неравенство в совокупность двух неравенств:
, а затем прибавить к границам πn. Раскрыв модуль, превратим неравенство в совокупность двух неравенств: 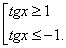 Дуги окружности, соответствующие их решениям, имеют вид:
Дуги окружности, соответствующие их решениям, имеют вид: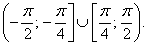 Обращаем внимание на то, что точки
Обращаем внимание на то, что точки 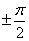 не входят в решение, поскольку при этих значениях аргумента тангенс не существует. Учитывая периодичность, находим окончательное решение:
не входят в решение, поскольку при этих значениях аргумента тангенс не существует. Учитывая периодичность, находим окончательное решение: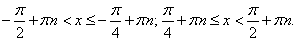 Ответ:
Ответ: 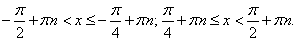 Комментарий. В более сложных неравенствах для их сведения к простейшим применяются в основном те же приемы, что и при решении уравнений.Пример 17.Решить неравенство:
Комментарий. В более сложных неравенствах для их сведения к простейшим применяются в основном те же приемы, что и при решении уравнений.Пример 17.Решить неравенство: 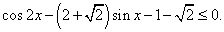 РешениеПредставим cos 2x = 1 — 2sin2 x и сделаем замену: t = sin x. Тогда для t требуется решить систему неравенств:
РешениеПредставим cos 2x = 1 — 2sin2 x и сделаем замену: t = sin x. Тогда для t требуется решить систему неравенств: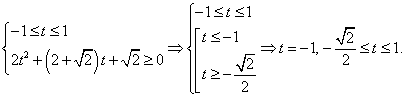 Обратная замена приводит к уравнению sin x = -1, откуда
Обратная замена приводит к уравнению sin x = -1, откуда 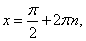 и неравенству
и неравенству 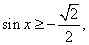 решение которого:
решение которого: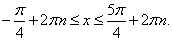 Ответ:
Ответ: 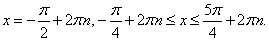 Пример 18.Решить неравенство:
Пример 18.Решить неравенство: 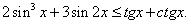 РешениеИспользуем то, что
РешениеИспользуем то, что 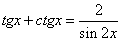 и сделаем замену: t = sin 2x. Неравенство для t имеет вид:
и сделаем замену: t = sin 2x. Неравенство для t имеет вид: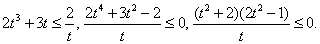 Методом интервалов находим решение:
Методом интервалов находим решение: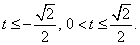 Проводим обратную замену и решаем полученные тригонометрические неравенства:Ответом будет объединение полученных промежутков.Ответ:
Проводим обратную замену и решаем полученные тригонометрические неравенства:Ответом будет объединение полученных промежутков.Ответ: 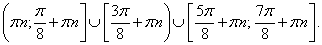 Пример 19.Решить неравенство:
Пример 19.Решить неравенство: 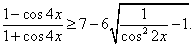 РешениеПреобразуем обе части неравенства.Сделаем замену:
РешениеПреобразуем обе части неравенства.Сделаем замену: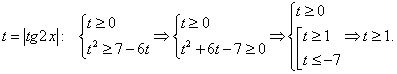 Следовательно, | tg 2x | ≥ 1, откуда:
Следовательно, | tg 2x | ≥ 1, откуда: 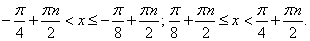 Ответ:
Ответ: 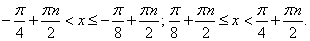 Пример 20.Решить неравенство:
Пример 20.Решить неравенство: 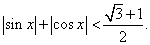 РешениеПоскольку обе части неравенства неотрицательны, можно возвести их в квадрат:
РешениеПоскольку обе части неравенства неотрицательны, можно возвести их в квадрат: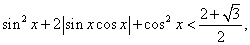 или
или 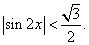 Еще раз возведем обе части в квадрат:
Еще раз возведем обе части в квадрат: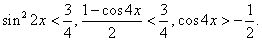 Получено простейшее тригонометрическое неравенство, решение которого:
Получено простейшее тригонометрическое неравенство, решение которого: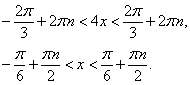 Ответ:
Ответ: 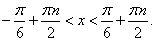 Видеолекция «Комбинированные неравенства»:
Видеолекция «Комбинированные неравенства»: 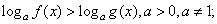
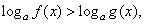 где
где 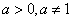
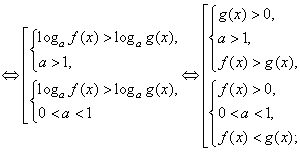
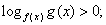
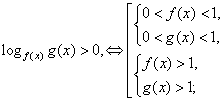
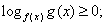
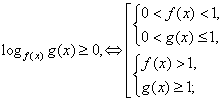
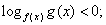
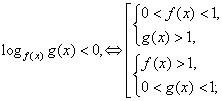
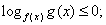
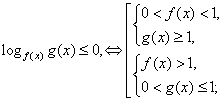
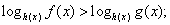
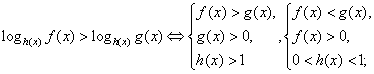
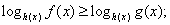
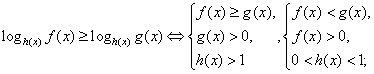
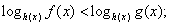
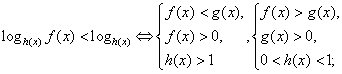
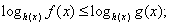
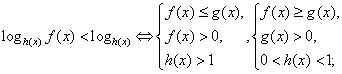
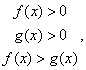 если a > 1;
если a > 1;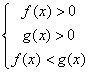 если 0 < a < 1.
если 0 < a < 1.