Иррациональные неравенства
является метод возведения в степень. При этом решение таких неравенств сводится к решению рациональных неравенств или систем рациональных неравенств.Пример 1.Решить неравенство: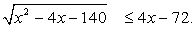 
Решение.Вспомним свойства неравенств: если обе части неравенства неотрицательны, то при возведении в квадрат знак неравенства не меняется; если отрицательны, то знак меняется на противоположный; если же левая и правая части имеют разные знаки, то возведение в квадрат является некорректной операцией.В данном неравенстве подкоренное выражение, разумеется, должно быть неотрицательным. Кроме того, значения правой части не меньше квадратного корня, то есть для решений неравенства правая часть может быть только неотрицательной. При выполнении этих условий мы имеем право возвести обе части в квадрат с сохранением знака неравенства: 
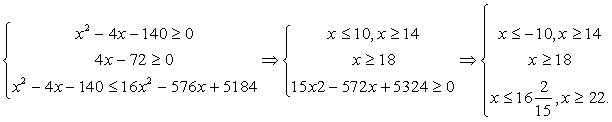Пересечение решений можно записать в виде: 
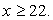Ответ: 
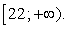Пример 2.Решить неравенство: 
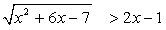Решение.В этом неравенстве, в отличие от предыдущего, правая часть может принимать значения разных знаков. Рассмотрим эти случаи отдельно.- Случай 1. Если выполнены условия
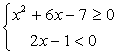, то неравенство будет верным: действительно, любое неотрицательное число больше любого отрицательного числа. Следовательно, все решения этой системы войдут в ответ. Решим полученную систему неравенств: 
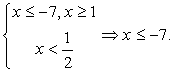Случай 2. Вторая возможность — выполнение условий: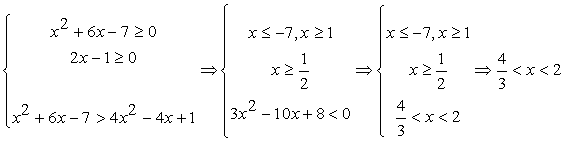 
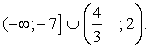Пример 3.Решить неравенство: 
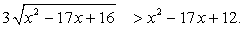Решение.Пусть 
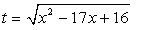, тогда значения t определяются системой неравенств: 
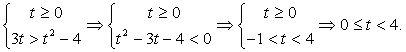После обратной замены получим: 
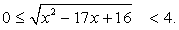Поскольку левая и правая части этого двойного неравенства неотрицательны, мы можем возвести все три части в квадрат: 
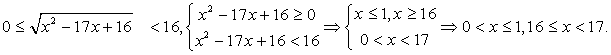Ответ: (0; 1] U [16; 17).Пример 4.Решить неравенство: 
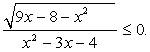Решение.- Во-первых,
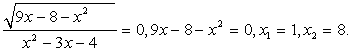Во-вторых, 
.
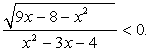Поскольку числитель дроби при всех допустимых значениях х неотрицателен, знаменатель должен принимать отрицательные значения, и неравенство сводится к системе: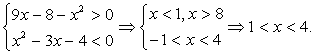 
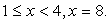.Еще раз обратите внимание на то, что если бы мы не рассматривали случай равенства отдельно, а решали систему неравенств 
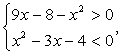то потеряли бы решение х = 8.Ответ: [1; 4), x = 8.Комментарий. Если корень четной степени входит в нестрогое неравенство в качестве множителя, то, чтобы избежать потери решений, лучше рассмотреть отдельно случай равенства и строгого неравенства. Видеолекция «Иррациональные неравенства»: 
