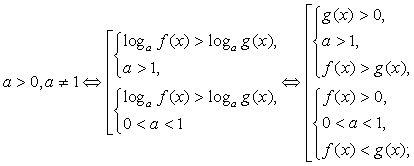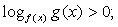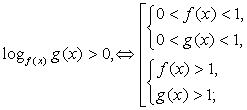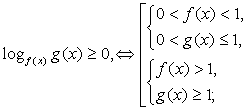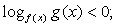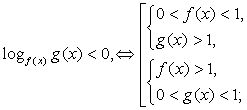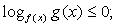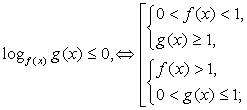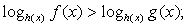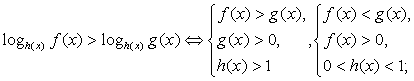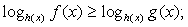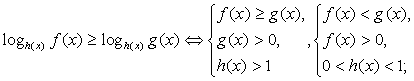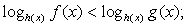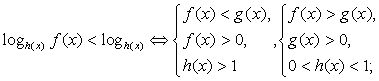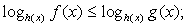Показательные неравенства
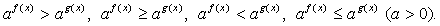 Важно помнить при этом, что при a > 1 можно перейти к неравенству, связывающему показатели степеней, знак которого совпадает со знаком исходного неравенства; при 0 < a < 1 показатели будут связаны неравенством противоположного знака. Т.е. если
Важно помнить при этом, что при a > 1 можно перейти к неравенству, связывающему показатели степеней, знак которого совпадает со знаком исходного неравенства; при 0 < a < 1 показатели будут связаны неравенством противоположного знака. Т.е. если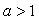 , то неравенства
, то неравенства 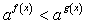 и
и 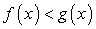 равносильны; если
равносильны; если 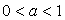 , то неравенства
, то неравенства 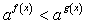 и
и 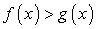 равносильны (это следует из того, что при
равносильны (это следует из того, что при 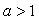 показательная функция возрастает, а при
показательная функция возрастает, а при 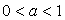 убывает).Составим схемы равносильных преобразований для решения неравенств следующего вида:Пример 1.Решить неравенство:
убывает).Составим схемы равносильных преобразований для решения неравенств следующего вида:Пример 1.Решить неравенство: 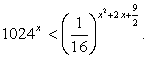 Решение.Представим обе части неравенства как степени с основанием 2:
Решение.Представим обе части неравенства как степени с основанием 2: 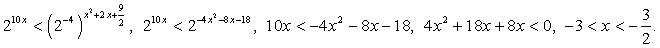 Ответ:
Ответ: 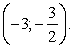 Пример 2.Решить неравенство:
Пример 2.Решить неравенство: 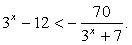 Решение.После замены t = 3x решим систему неравенств:
Решение.После замены t = 3x решим систему неравенств: 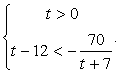 Поскольку знаменатель дроби в правой части второго неравенства при t > 0 положителен, можно умножить на него обе части неравенства, превратив его в квадратное:
Поскольку знаменатель дроби в правой части второго неравенства при t > 0 положителен, можно умножить на него обе части неравенства, превратив его в квадратное: 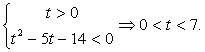 Сделаем обратную замену:
Сделаем обратную замену: 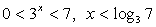 (левая часть неравенства верна при любом х).Ответ:
(левая часть неравенства верна при любом х).Ответ: 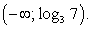 Пример 3.Решить неравенство:
Пример 3.Решить неравенство: 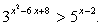 Решение.Перейдем к основанию 3:
Решение.Перейдем к основанию 3: 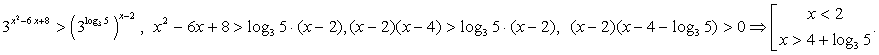 Ответ:
Ответ: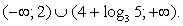 Пример 4.Решить неравенство:
Пример 4.Решить неравенство: 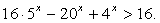 Решение.Перенесем все слагаемые в левую часть и разложим ее на множители:(16 – 4x)(5x – 1) > 0. Найдем корни левой части неравенства:
Решение.Перенесем все слагаемые в левую часть и разложим ее на множители:(16 – 4x)(5x – 1) > 0. Найдем корни левой части неравенства:- 1 случай. 16 – 4х = 0, х = 2.2 случай. 5х – 1 = 0, х = 0.
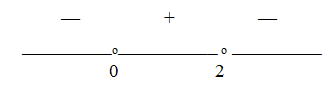 Итак, 0 < x < 2.Ответ: (0; 2).Пример 5.Решить неравенство:
Итак, 0 < x < 2.Ответ: (0; 2).Пример 5.Решить неравенство: 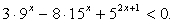 Решение.Запишем неравенство в виде:
Решение.Запишем неравенство в виде: 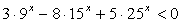 и разделим обе его части на 25x(при делении на положительное число знак неравенства не изменится):
и разделим обе его части на 25x(при делении на положительное число знак неравенства не изменится): 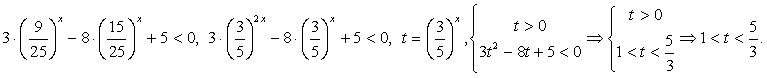 Сделаем обратную замену:
Сделаем обратную замену: 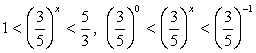 . Поскольку основание степени меньше 1, при переходе к показателям знак неравенства меняется: - 1 < x < 0.Ответ: (- 1; 0).Пример 6.Решить неравенство:
. Поскольку основание степени меньше 1, при переходе к показателям знак неравенства меняется: - 1 < x < 0.Ответ: (- 1; 0).Пример 6.Решить неравенство: 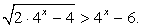 Решение.Замена t = 4x превращает неравенство в иррациональное:
Решение.Замена t = 4x превращает неравенство в иррациональное: 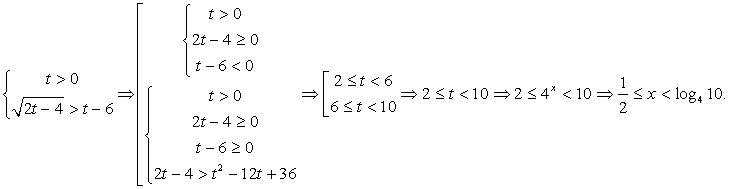 Ответ:
Ответ: 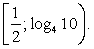 Видеолекция «Показательные неравенства»:
Видеолекция «Показательные неравенства»: 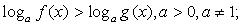
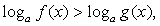 где
где