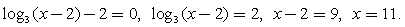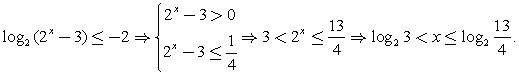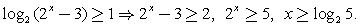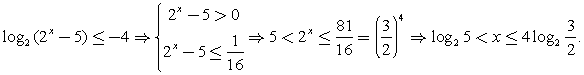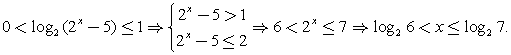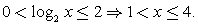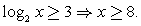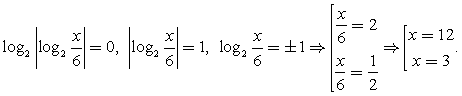Логарифмические неравенства
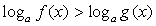 сводится к одной из двух систем неравенств:Пример 1.Решить неравенство:
сводится к одной из двух систем неравенств:Пример 1.Решить неравенство: 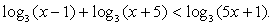 Решение.Используя свойства логарифмов, преобразуем левую часть:
Решение.Используя свойства логарифмов, преобразуем левую часть: 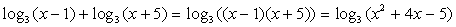 и решим систему неравенств:
и решим систему неравенств: 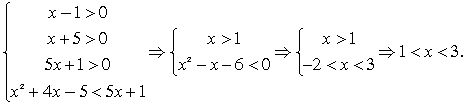 Обращаем ваше внимание на то, что положительным должно быть каждое логарифмируемое выражение, а не только их произведение.Ответ: (1; 3).Пример 2.Решить неравенство:
Обращаем ваше внимание на то, что положительным должно быть каждое логарифмируемое выражение, а не только их произведение.Ответ: (1; 3).Пример 2.Решить неравенство: 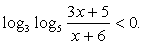 Решение.Поскольку
Решение.Поскольку  решаем неравенство
решаем неравенство 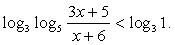 Оно равносильно системе:
Оно равносильно системе: 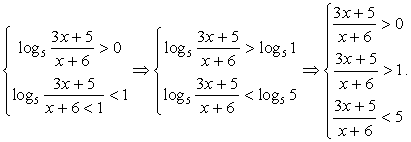 Заметим, что первое неравенство можно не решать, так как оно заведомо будет верным для всех решений второго неравенства. Тогда
Заметим, что первое неравенство можно не решать, так как оно заведомо будет верным для всех решений второго неравенства. Тогда 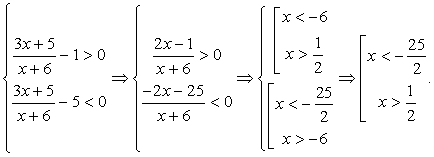 Ответ:
Ответ: 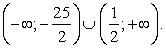 Составим схемы равносильных преобразований для решения неравенств следующего вида:Комментарий. Если основание логарифма переменно и может принимать значения как меньшие, так и большие 1, нужно рассмотреть эти ситуации отдельно, так как в первом случае знак неравенства не меняется при переходе к аргументам, а во втором – меняется на обратный.Пример 3.Решить неравенство:
Составим схемы равносильных преобразований для решения неравенств следующего вида:Комментарий. Если основание логарифма переменно и может принимать значения как меньшие, так и большие 1, нужно рассмотреть эти ситуации отдельно, так как в первом случае знак неравенства не меняется при переходе к аргументам, а во втором – меняется на обратный.Пример 3.Решить неравенство: 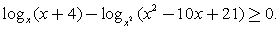 Решение.Запишем неравенство в виде:
Решение.Запишем неравенство в виде: 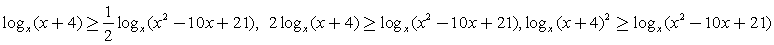 (учитываем, что x > 0, поэтому
(учитываем, что x > 0, поэтому 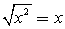 ).Ответ:
).Ответ: 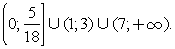 Пример 4.Решить неравенство:
Пример 4.Решить неравенство: 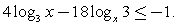 Решение.Пусть
Решение.Пусть 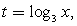 тогда
тогда 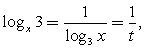 и для t получаем неравенство:
и для t получаем неравенство: 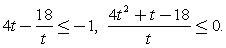 Не забудьте, что в дробно-рациональном неравенстве важен знак не только числителя, но и знаменателя дроби, и решать его лучше всего методом интервалов (самая распространенная ошибка на этом этапе решения – «отбрасывание» знаменателя). Корни числителя:
Не забудьте, что в дробно-рациональном неравенстве важен знак не только числителя, но и знаменателя дроби, и решать его лучше всего методом интервалов (самая распространенная ошибка на этом этапе решения – «отбрасывание» знаменателя). Корни числителя: 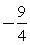 и 2, корень знаменателя – 0, и знак дроби распределяется на интервалах так:
и 2, корень знаменателя – 0, и знак дроби распределяется на интервалах так: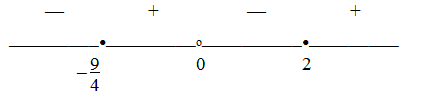 Следовательно,
Следовательно, 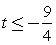 или
или 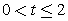 (корень знаменателя, разумеется, в ответ не входит).1 случай.
(корень знаменателя, разумеется, в ответ не входит).1 случай. 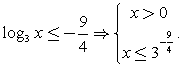 2 случай.
2 случай. 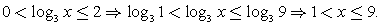 Ответ:
Ответ: 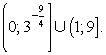 Пример 5.Решить неравенство:
Пример 5.Решить неравенство: 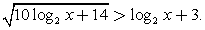 Сделаем замену: t = log2 x и решим для t иррациональное неравенство
Сделаем замену: t = log2 x и решим для t иррациональное неравенство 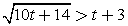 :Обратная замена:
:Обратная замена: 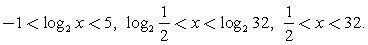 Ответ:
Ответ: 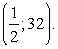 Пример 6.Решить неравенство:
Пример 6.Решить неравенство: 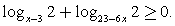 Решение.Определим ОДЗ:
Решение.Определим ОДЗ: 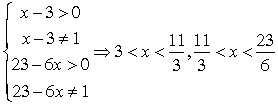 и перейдем в обоих логарифмах к основанию 2:
и перейдем в обоих логарифмах к основанию 2: 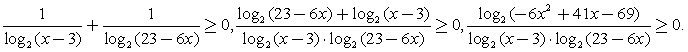 Найдем корни числителя и знаменателя:
Найдем корни числителя и знаменателя: (само это значение тоже не входит в ОДЗ, но слева и справа от него определены все функции, присутствующие в неравенстве, и один из множителей знаменателя в этой точке меняет знак).Итак, в рамках ОДЗ дробь меняет знак трижды: в точках
(само это значение тоже не входит в ОДЗ, но слева и справа от него определены все функции, присутствующие в неравенстве, и один из множителей знаменателя в этой точке меняет знак).Итак, в рамках ОДЗ дробь меняет знак трижды: в точках 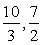 и
и 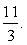 Расставим знаки на интервалах. При
Расставим знаки на интервалах. При 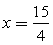 (точка, расположенная на самом правом интервале) х – 3 = 0,75 < 1, 23 – 6x = 0,5 < 1, - 6x2 + 41x – 69 = 0,375 < 1, поэтому все три логарифма, входящие в последнюю форму неравенства, отрицательны; соответственно, отрицательна и сама дробь.
(точка, расположенная на самом правом интервале) х – 3 = 0,75 < 1, 23 – 6x = 0,5 < 1, - 6x2 + 41x – 69 = 0,375 < 1, поэтому все три логарифма, входящие в последнюю форму неравенства, отрицательны; соответственно, отрицательна и сама дробь.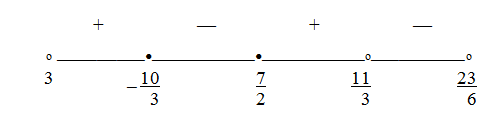 Ответ:
Ответ: 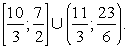 Пример 7.Решить неравенство:
Пример 7.Решить неравенство: 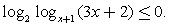 Решение.Превратим простейшее неравенство
Решение.Превратим простейшее неравенство 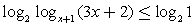 в систему:
в систему: 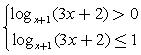 и перейдем к любому постоянному основанию (например, 2):
и перейдем к любому постоянному основанию (например, 2): 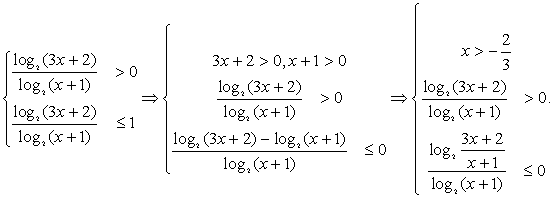 Решим второе и третье неравенства методом интервалов.
Решим второе и третье неравенства методом интервалов.- 1 случай.
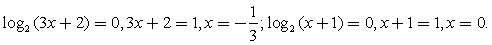
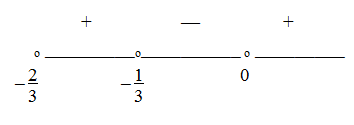 Решение второго неравенства:
Решение второго неравенства: 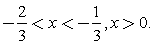 2 случай.
2 случай. 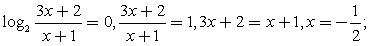 корень знаменателя (х = 0) тот же, что в предыдущем неравенстве.
корень знаменателя (х = 0) тот же, что в предыдущем неравенстве.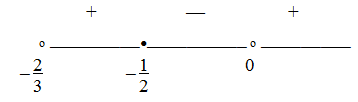 Решение:
Решение: 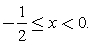
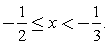 Ответ:
Ответ: 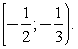 Пример 8.Решить неравенство:
Пример 8.Решить неравенство: 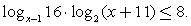 Решение.ОДЗ:
Решение.ОДЗ: 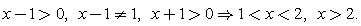 Преобразуем первый логарифм:
Преобразуем первый логарифм: 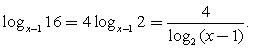 Тогда
Тогда 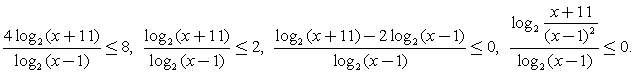 Решим полученное неравенство методом интервалов:Расставим знаки (при х = 10, то есть на самом правом из полученных промежутков, числитель дроби отрицателен, а знаменатель положителен, то есть вся дробь отрицательна).
Решим полученное неравенство методом интервалов:Расставим знаки (при х = 10, то есть на самом правом из полученных промежутков, числитель дроби отрицателен, а знаменатель положителен, то есть вся дробь отрицательна).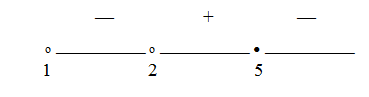 Ответ:
Ответ: 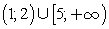 .Пример 9.Решить неравенство:
.Пример 9.Решить неравенство: 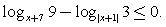 Решение.Найдем ОДЗ:
Решение.Найдем ОДЗ: 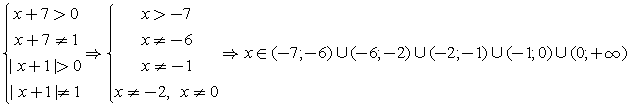 .Перейдем к основанию 3:
.Перейдем к основанию 3: 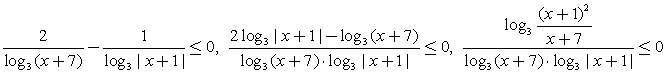 (учитываем, что | x + 1 |2 = ( x + 1 )2).Применим метод интервалов:Отметим, что из всех изолированных точек, не входящих в ОДЗ, только х = - 1 не является корнем числителя или знаменателя; соответственно в этой точке знак дроби не меняется.Расставим знаки, учитывая, что на самом правом интервале все логарифмы, входящие в левую часть неравенства, положительны:
(учитываем, что | x + 1 |2 = ( x + 1 )2).Применим метод интервалов:Отметим, что из всех изолированных точек, не входящих в ОДЗ, только х = - 1 не является корнем числителя или знаменателя; соответственно в этой точке знак дроби не меняется.Расставим знаки, учитывая, что на самом правом интервале все логарифмы, входящие в левую часть неравенства, положительны: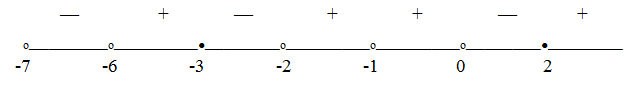 Ответ: (- 7; - 6)U[ - 3; - 2)U(0; 2].Комментарий. При решении подобных неравенств применяются те же приемы, что и при решении уравнений аналогичного типа (замены, логарифмирование, потенцирование). Как всегда, внимательно следите за ограничениями на ОДЗ.Пример 10.Решить неравенство: log3 (3x – 3) + x < log3 10.Решение.Представим x = log3 3x, сделаем замену t = 3x и решим для t систему неравенств с учетом ОДЗ:
Ответ: (- 7; - 6)U[ - 3; - 2)U(0; 2].Комментарий. При решении подобных неравенств применяются те же приемы, что и при решении уравнений аналогичного типа (замены, логарифмирование, потенцирование). Как всегда, внимательно следите за ограничениями на ОДЗ.Пример 10.Решить неравенство: log3 (3x – 3) + x < log3 10.Решение.Представим x = log3 3x, сделаем замену t = 3x и решим для t систему неравенств с учетом ОДЗ: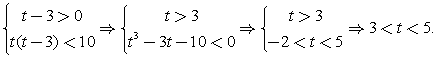 Обратная замена:
Обратная замена: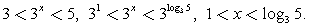 Ответ: (1; log3 5).Пример 11.Решим неравенство:
Ответ: (1; log3 5).Пример 11.Решим неравенство: 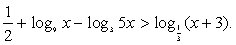 Решение.
Решение.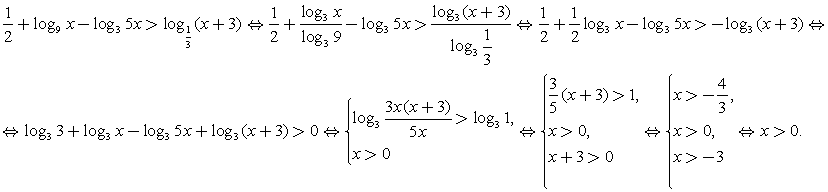 Таким образом, решение исходного неравенства:
Таким образом, решение исходного неравенства: 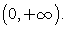 Ответ:
Ответ: 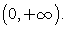 Пример 12.Решим неравенство:
Пример 12.Решим неравенство: 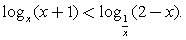 Решение.
Решение.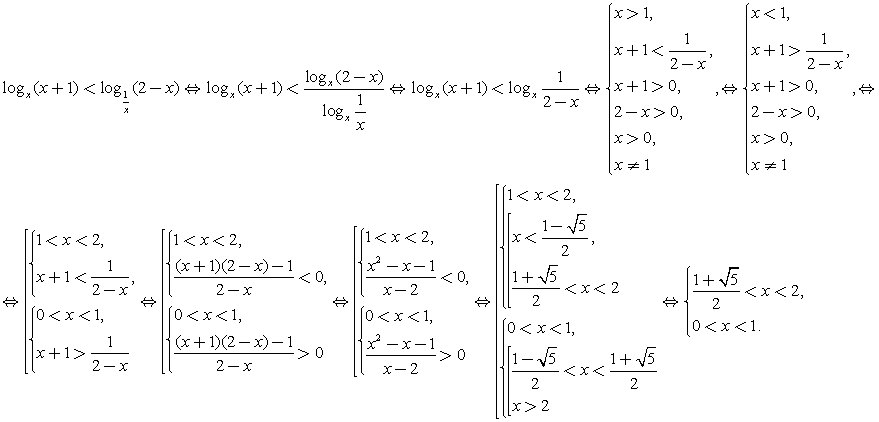 Таким образом, решение исходного неравенства:
Таким образом, решение исходного неравенства: 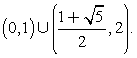 Ответ:
Ответ: 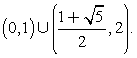 Пример 13.Решить неравенство:
Пример 13.Решить неравенство: 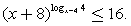 Решение.Вновь перед нами в левой части выражение вида
Решение.Вновь перед нами в левой части выражение вида 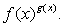 Наиболее удобный прием для упрощения – логарифмирование. Прологарифмируем обе части по основанию 4 и составим систему неравенств с учетом ОДЗ:
Наиболее удобный прием для упрощения – логарифмирование. Прологарифмируем обе части по основанию 4 и составим систему неравенств с учетом ОДЗ: 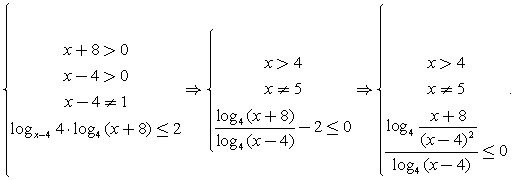 Решим последнее неравенство методом интервалов.При достаточно больших значениях х аргумент логарифма, стоящего в числителе, меньше 1, то есть числитель дроби отрицателен, а знаменатель положителен. С учетом этого расставим знаки на интервалах:
Решим последнее неравенство методом интервалов.При достаточно больших значениях х аргумент логарифма, стоящего в числителе, меньше 1, то есть числитель дроби отрицателен, а знаменатель положителен. С учетом этого расставим знаки на интервалах: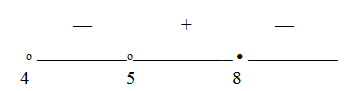 Таким образом, 4 < x < 5 или
Таким образом, 4 < x < 5 или 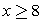 .Ответ:
.Ответ: 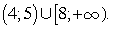 Пример 14.Решить неравенство:
Пример 14.Решить неравенство: 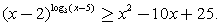 Решение.Задаем ОДЗ и логарифмируем обе части по основанию 3:
Решение.Задаем ОДЗ и логарифмируем обе части по основанию 3: 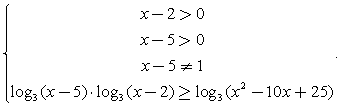 Заметим, что х2 – 10х + 25 = (х – 5)2. Тогда
Заметим, что х2 – 10х + 25 = (х – 5)2. Тогда 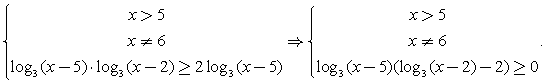 Последнее неравенство решаем методом интервалов.Расставим знаки на интервалах (при x > 11 левая часть положительна):
Последнее неравенство решаем методом интервалов.Расставим знаки на интервалах (при x > 11 левая часть положительна):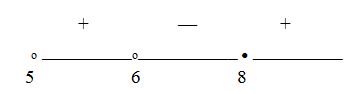 Ответ:
Ответ: 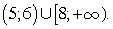 .Пример 15.Решить неравенство:
.Пример 15.Решить неравенство: 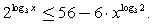 Решение.Воспользуемся одним из свойств логарифмов (см. занятие 13):
Решение.Воспользуемся одним из свойств логарифмов (см. занятие 13): 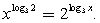 Неравенство сразу резко упрощается:
Неравенство сразу резко упрощается: 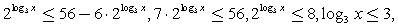 и, с учетом ОДЗ,
и, с учетом ОДЗ, 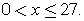 Ответ: (0; 27].Пример 16.Решить неравенство:Решение.Упростим второй множитель левой части: Этот результат позволяет сделать замену: t = log2 (2x – 3) и решать неравенство:
Ответ: (0; 27].Пример 16.Решить неравенство:Решение.Упростим второй множитель левой части: Этот результат позволяет сделать замену: t = log2 (2x – 3) и решать неравенство: 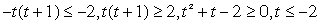 или
или 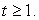 Сделаем обратную замену.Ответ:
Сделаем обратную замену.Ответ: 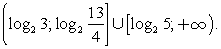 Пример 17.Решить неравенство:
Пример 17.Решить неравенство: 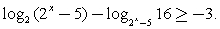 Решение.Замена:
Решение.Замена: 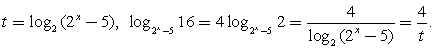 Решим неравенство для
Решим неравенство для 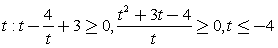 или
или 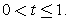 Обратная замена:Ответ:
Обратная замена:Ответ: 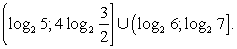 Пример 18.Решить неравенство:
Пример 18.Решить неравенство: 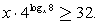 Решение.Учтем ОДЗ:
Решение.Учтем ОДЗ: 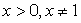 и прологарифмируем обе части по основанию 2:
и прологарифмируем обе части по основанию 2: 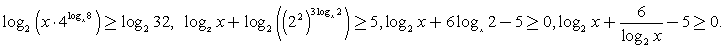 Замена:
Замена: 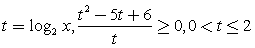 или
или 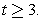 Ответ:
Ответ: 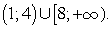 Пример 19.Решить неравенство:
Пример 19.Решить неравенство: 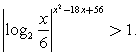 Решение.ОДЗ:
Решение.ОДЗ: 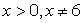 (подмодульное выражение не должно равняться нулю). Прологарифмируем обе части по основанию 2:
(подмодульное выражение не должно равняться нулю). Прологарифмируем обе части по основанию 2: 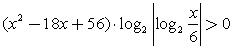 и решим полученное неравенство методом интервалов.Расставим знаки на интервалах, учитывая, что при x > 14 левая часть неравенства положительна, а при х = 6 ни один из множителей не меняет знак:
и решим полученное неравенство методом интервалов.Расставим знаки на интервалах, учитывая, что при x > 14 левая часть неравенства положительна, а при х = 6 ни один из множителей не меняет знак: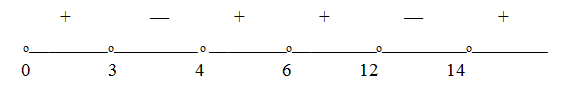 Ответ:
Ответ: 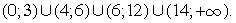 Видеолекция «Логарифмические неравенства»:
Видеолекция «Логарифмические неравенства»: 
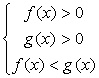 ,
, 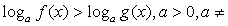
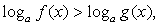 где
где 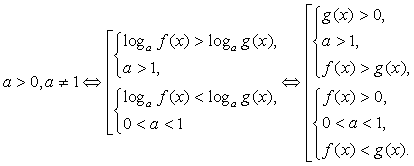
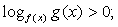
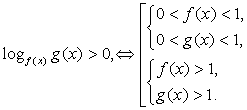
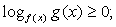
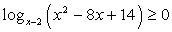
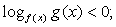
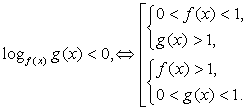
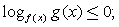
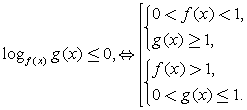
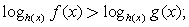
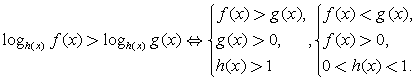
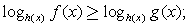
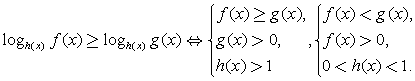
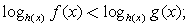
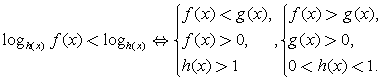
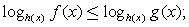
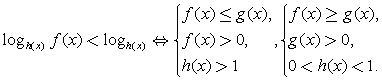
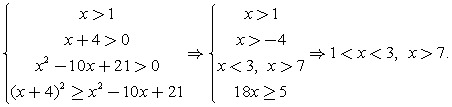
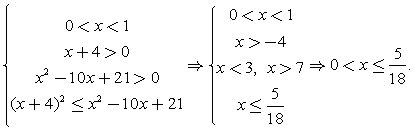
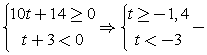 решений нет.
решений нет.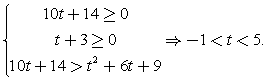
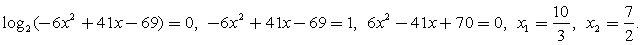
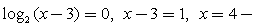 не входит в ОДЗ.
не входит в ОДЗ.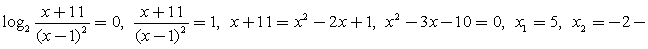 не входит в ОДЗ.
не входит в ОДЗ.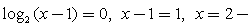 точка, лежащая внутри ОДЗ.
точка, лежащая внутри ОДЗ.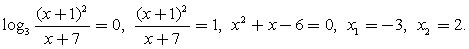
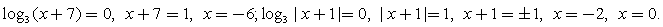
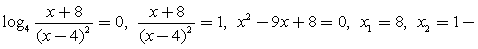 не входит в ОДЗ.
не входит в ОДЗ.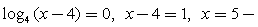 точка лежит внутри ОДЗ, знак дроби в ней меняется.
точка лежит внутри ОДЗ, знак дроби в ней меняется.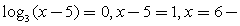 сама эта точка в ОДЗ не входит, но знак первого множителя в ней меняется.
сама эта точка в ОДЗ не входит, но знак первого множителя в ней меняется.