Рациональные неравенства
 применяют так называемый метод интервалов
применяют так называемый метод интервалов . Практика вступительных испытаний по математике показывает, что абитуриенты не всегда правильно используют этот метод, понимают его сущность и специфику. В значительной степени это связано с тем, что в учебной литературе встречаются различные подходы к изложению метода интервалов, далеко не всегда удачные. Имеет место путаница с терминами, «странные синтезы», сразу нескольких подходов. Но алгоритм метода интервал требует строгости и четкости.Будем понимать метод интервалов, как метод, применяемых для решения рациональных неравенств строго определенного вида:
. Практика вступительных испытаний по математике показывает, что абитуриенты не всегда правильно используют этот метод, понимают его сущность и специфику. В значительной степени это связано с тем, что в учебной литературе встречаются различные подходы к изложению метода интервалов, далеко не всегда удачные. Имеет место путаница с терминами, «странные синтезы», сразу нескольких подходов. Но алгоритм метода интервал требует строгости и четкости.Будем понимать метод интервалов, как метод, применяемых для решения рациональных неравенств строго определенного вида: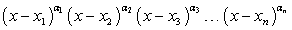 V 0,где x1, x2 , x3, …, xn ϵ
R; ?1, ?2, ?3,…, ?n ϵ
N и V — любой из знаков неравенства >
, <
, ≥
, ≤
.Если данное неравенство не соответствует указанному виду, то его необходимо привести к этому виду теми или иными равносильными преобразованиями, и лишь затем применять метод интервалов. Назовем указанный вид неравенства стандартным для решения методом интервалов.Введем еще два термина. Пусть
V 0,где x1, x2 , x3, …, xn ϵ
R; ?1, ?2, ?3,…, ?n ϵ
N и V — любой из знаков неравенства >
, <
, ≥
, ≤
.Если данное неравенство не соответствует указанному виду, то его необходимо привести к этому виду теми или иными равносильными преобразованиями, и лишь затем применять метод интервалов. Назовем указанный вид неравенства стандартным для решения методом интервалов.Введем еще два термина. Пусть 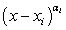 — множитель, входящий в неравенство, стандартное для решения методом интервалов. Если показатель степени ?i — нечетное число, то точку х = xi будем называть простой
— множитель, входящий в неравенство, стандартное для решения методом интервалов. Если показатель степени ?i — нечетное число, то точку х = xi будем называть простой . Если показатель степени ?i — четное число, то точку х = xi будем называть двойной
. Если показатель степени ?i — четное число, то точку х = xi будем называть двойной .Теперь сформулируем алгоритм метода интервалов.Пусть дано неравенство вида, стандартного для решения методом интервалов. Для его решения:
.Теперь сформулируем алгоритм метода интервалов.Пусть дано неравенство вида, стандартного для решения методом интервалов. Для его решения:- 1) отметим на числовой прямой точки, соответствующие числам x1, x2, x3,…, xn, разбив тем самым всю числовую прямую на промежутки (интервалы); причем, если знак неравенства строгий, то точки отмечаются выколотыми, если знак неравенства нестрогий, то точки отмечаются сплошными;2) на каждом из полученных промежутков выражение
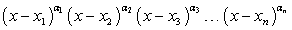 будет сохранять свой знак постоянным; расставим эти знаки пользуясь правилом чередования знаков:
будет сохранять свой знак постоянным; расставим эти знаки пользуясь правилом чередования знаков:- а) в крайнем правом интервале всегда знак «плюс»;б) при переходе через простую точку знак меняется, на противоположный;в) при переходе через двойную точку знак сохраняется;
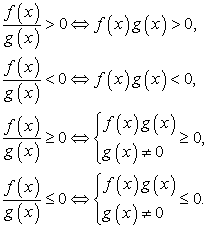 Подведем итог. Для применения метода нужно преобразовать неравенство так, чтобы в правой его части стоял 0, а левая была произведением нескольких множителей или дробью, числитель и знаменатель которой разложены на множители. Затем находятся корни каждого множителя (то есть от решения неравенства вы переходите к решению уравнений), и среди них выделяются такие, в которых ни один из имеющихся множителей не меняет знак, или меняет знак четное количество множителей. В дальнейшем такие корни, если они найдутся, мы будем называть кратными
Подведем итог. Для применения метода нужно преобразовать неравенство так, чтобы в правой его части стоял 0, а левая была произведением нескольких множителей или дробью, числитель и знаменатель которой разложены на множители. Затем находятся корни каждого множителя (то есть от решения неравенства вы переходите к решению уравнений), и среди них выделяются такие, в которых ни один из имеющихся множителей не меняет знак, или меняет знак четное количество множителей. В дальнейшем такие корни, если они найдутся, мы будем называть кратными (хотя это не совсем точно). Для окончательного решения неравенства остается нанести найденные корни на числовую прямую, найти знак левой части неравенства только на одном интервале, ограниченном полученными точками, и расставить знаки на остальных интервалах, меняя их при переходе через простой корень
(хотя это не совсем точно). Для окончательного решения неравенства остается нанести найденные корни на числовую прямую, найти знак левой части неравенства только на одном интервале, ограниченном полученными точками, и расставить знаки на остальных интервалах, меняя их при переходе через простой корень и не меняя при переходе через кратный.Пример 1.Решим неравенство:
и не меняя при переходе через кратный.Пример 1.Решим неравенство: 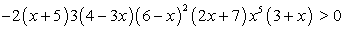 Решение.Приведем данное неравенство к виду стандартному для решения методом интервалов:
Решение.Приведем данное неравенство к виду стандартному для решения методом интервалов: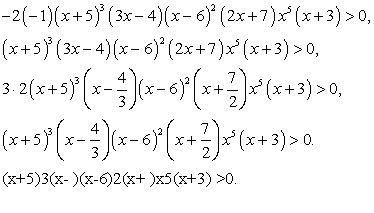 Построим разбиение числовой прямой на промежутки.
Построим разбиение числовой прямой на промежутки. Заметим, что масштаб в данном случае соблюдать совсем необязательно, но отдельные принципиальные детали, относящиеся к уровню общей графической культуры, соблюдать конечно следует. Так, точка -3 должна быть изображена более удаленной от нуля, чем точка
Заметим, что масштаб в данном случае соблюдать совсем необязательно, но отдельные принципиальные детали, относящиеся к уровню общей графической культуры, соблюдать конечно следует. Так, точка -3 должна быть изображена более удаленной от нуля, чем точка 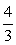 , а расстояние между точками
, а расстояние между точками 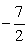 и -3 должно быть значительно меньше, чем расстояние между точками
и -3 должно быть значительно меньше, чем расстояние между точками 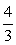 и 6 и т.д.) Расставим знаки в промежутках, используя правило чередования.
и 6 и т.д.) Расставим знаки в промежутках, используя правило чередования. Из рисунка видно решение неравенства:
Из рисунка видно решение неравенства: 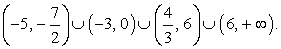 Ответ:
Ответ: 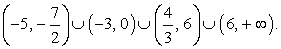 Пример 2.Решим неравенство:
Пример 2.Решим неравенство: 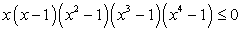 .Решение.Раскроем скобки; имеем:
.Решение.Раскроем скобки; имеем: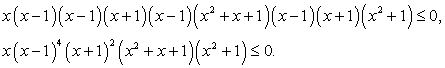 Так как x2 + х + 1 >
0 при всех х и x2 + 1 >
0 при всех х, то получаем неравенство вида, стандартного для решения методом интервалов и равносильное исходному неравенству:
Так как x2 + х + 1 >
0 при всех х и x2 + 1 >
0 при всех х, то получаем неравенство вида, стандартного для решения методом интервалов и равносильное исходному неравенству: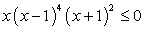 Построим разбиение числовой прямой на промежутки и расставим знаки по правилу чередования.
Построим разбиение числовой прямой на промежутки и расставим знаки по правилу чередования. Таким образом, решение неравенства:
Таким образом, решение неравенства: 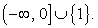 Ответ:
Ответ: 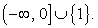 Комментарий. На материал, следующий ниже, советуем обратить особое внимание, поскольку в школе ему редко уделяют должное внимание.Значительно содействуют пониманию сущности метода интервалов, а значит и лучшему его применению упражнения на конструирование неравенств по заданным объединениям промежутков — их решениям. Рассмотрим пример. Рассмотрим пример 3.Пример 3.Составим неравенство, решение которого (-?, -10) U [-7, -4] U (-4, 2) U {6} U [11, +?].Решение.Прежде всего, отметим все необходимые точки на числовой прямой.
Комментарий. На материал, следующий ниже, советуем обратить особое внимание, поскольку в школе ему редко уделяют должное внимание.Значительно содействуют пониманию сущности метода интервалов, а значит и лучшему его применению упражнения на конструирование неравенств по заданным объединениям промежутков — их решениям. Рассмотрим пример. Рассмотрим пример 3.Пример 3.Составим неравенство, решение которого (-?, -10) U [-7, -4] U (-4, 2) U {6} U [11, +?].Решение.Прежде всего, отметим все необходимые точки на числовой прямой. Теперь произвольно выберем знак составляемого неравенства (ясно, что этот знак нестрогого неравенства
Теперь произвольно выберем знак составляемого неравенства (ясно, что этот знак нестрогого неравенства , поскольку на нашем рисунке есть сплошные точки
, поскольку на нашем рисунке есть сплошные точки ) и в соответствии с данным решением неравенства расставим знаки. Итак, пусть знак нашего неравенства ≥
, тогда имеем.
) и в соответствии с данным решением неравенства расставим знаки. Итак, пусть знак нашего неравенства ≥
, тогда имеем. Из рисунка видно, что точки х = -10, х = -7, х = 2 и х = 11 — простые точки, а точки х = -4, х = 6 — двойные точки
Из рисунка видно, что точки х = -10, х = -7, х = 2 и х = 11 — простые точки, а точки х = -4, х = 6 — двойные точки . Кроме того, поскольку на рисунке есть и выколотые
. Кроме того, поскольку на рисунке есть и выколотые и сплошные точки
и сплошные точки , то составляемое неравенство — дробное рациональное
, то составляемое неравенство — дробное рациональное . Учитывая все эти выводы, получаем, например:
. Учитывая все эти выводы, получаем, например: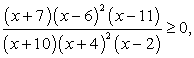 или, если перемножить скобки:
или, если перемножить скобки: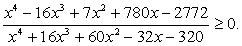 Ответ:
Ответ: 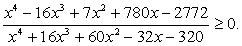 Рациональные неравенства в работах ЕГЭ часто «усложнены модулями»
Рациональные неравенства в работах ЕГЭ часто «усложнены модулями» . Неравенства, содержащие переменную под знаком модуля, не входят явно в школьную программу по математике, часто предлагаются школьными учителями как задания повышенной сложности. В итоге, вызывая у абитуриентов страх и трепет, такие задания многими абитуриентами просто пропускаются, хотя вполне могли быть выполнены. Для этого необходимо не так много:
. Неравенства, содержащие переменную под знаком модуля, не входят явно в школьную программу по математике, часто предлагаются школьными учителями как задания повышенной сложности. В итоге, вызывая у абитуриентов страх и трепет, такие задания многими абитуриентами просто пропускаются, хотя вполне могли быть выполнены. Для этого необходимо не так много:- 1) четко знать определение модуля;2) понимать суть приема решения уравнений и неравенств, основанного на одновременном раскрытии всех модулей (причем, здесь достаточно конкретных примеров);3) помнить о методе введения новой переменной.
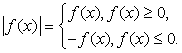 Модули, входящие в уравнение или неравенство раскрываются по определению и в дальнейшем уже решаются уравнения и неравенства, не содержащие модуля. Заметим, что абитуриенты часто вместо равенства, указанного выше, применяют равенство:
Модули, входящие в уравнение или неравенство раскрываются по определению и в дальнейшем уже решаются уравнения и неравенства, не содержащие модуля. Заметим, что абитуриенты часто вместо равенства, указанного выше, применяют равенство: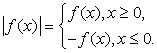 Понятно, что оно справедливо лишь в случае f(x) = x. В общем случае это равенство неверно. Следует помнить об этом и не допускать этой распространенной среди абитуриентов ошибки.Решение дробно-рациональных уравнений нередко сводится к решению обычных квадратных уравнений
Понятно, что оно справедливо лишь в случае f(x) = x. В общем случае это равенство неверно. Следует помнить об этом и не допускать этой распространенной среди абитуриентов ошибки.Решение дробно-рациональных уравнений нередко сводится к решению обычных квадратных уравнений , но с учетом ограничений на допустимые значения неизвестного. В частности, из ОДЗ исключаются те значения х, при которых хотя бы один из знаменателей дробей, входящих в уравнение, обращается в 0.Основной прием решения модульных уравнений и неравенств — раскрытие модуля с использованием его определения (|a| = a при a ≥
0 и |a| = -a при a <
0). Для этого обычно рассматривают отдельно два случая: случай, когда подмодульное выражение неотрицательно и когда оно отрицательно.Пример 4.Решим неравенство:
, но с учетом ограничений на допустимые значения неизвестного. В частности, из ОДЗ исключаются те значения х, при которых хотя бы один из знаменателей дробей, входящих в уравнение, обращается в 0.Основной прием решения модульных уравнений и неравенств — раскрытие модуля с использованием его определения (|a| = a при a ≥
0 и |a| = -a при a <
0). Для этого обычно рассматривают отдельно два случая: случай, когда подмодульное выражение неотрицательно и когда оно отрицательно.Пример 4.Решим неравенство: 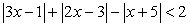 Решение.Раскроем модули:
Решение.Раскроем модули: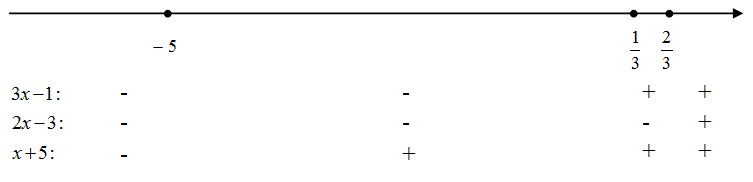 Таким образом, имеем:1)
Таким образом, имеем:1) 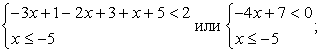 2)
2) 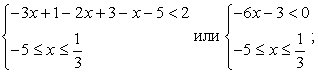 3)
3) 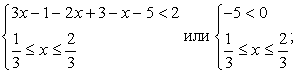 4)
4) 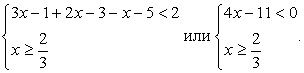 Решение неравенства свелось к решению совокупности систем неравенств:
Решение неравенства свелось к решению совокупности систем неравенств: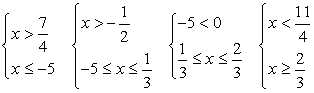 .Следовательно, решение данного неравенства:
.Следовательно, решение данного неравенства: 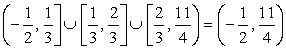 Ответ:
Ответ: 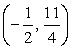 .Пример 5.Решим неравенство:
.Пример 5.Решим неравенство: 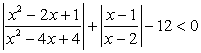 .Решение.Пусть
.Решение.Пусть 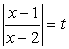 , тогда t2 + t – 12 <
0, имеем (t + 4 )(t - 3) <
0.Решение последнего неравенства — интервал (-4, 3). Таким образом, решение данного неравенства сводится к решению двойного неравенства:
, тогда t2 + t – 12 <
0, имеем (t + 4 )(t - 3) <
0.Решение последнего неравенства — интервал (-4, 3). Таким образом, решение данного неравенства сводится к решению двойного неравенства: 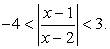 Поскольку
Поскольку 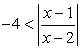 при всех допустимых значениях х, то осталось решить лишь неравенство
при всех допустимых значениях х, то осталось решить лишь неравенство 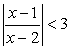 . Отметим на числовой прямой х = 1 — точку, зануляющую подмодульное выражение, и х = 2 — точку, в которой подмодульное выражение не существует. Расставим знаки подмодульного выражения в каждом из трех полученных промежутков:
. Отметим на числовой прямой х = 1 — точку, зануляющую подмодульное выражение, и х = 2 — точку, в которой подмодульное выражение не существует. Расставим знаки подмодульного выражения в каждом из трех полученных промежутков:  Таким образом, мы имеем два случая:Решение неравенства сводится, таким образом, к решению совокупности систем:
Таким образом, мы имеем два случая:Решение неравенства сводится, таким образом, к решению совокупности систем: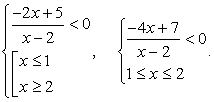 Решение первой системы:
Решение первой системы: 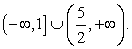 Решение второй системы:
Решение второй системы: 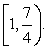 Таким образом, решение данного неравенства:
Таким образом, решение данного неравенства: 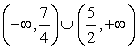 .Ответ:
.Ответ: 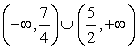 .Решение дробно-рациональных неравенствХочется сразу предостеречь вас от самой распространенной ошибки: умножения обеих частей неравенства на общий знаменатель. Если при разных значениях х знаменатель может менять знак, то избавляться от него нельзя. Почему? Потому что при умножении обеих частей неравенства на положительное число знак неравенства не меняется, а на отрицательное — меняется на обратный. Поэтому, решая такое неравенство, вы должны учитывать знак не только числителя, но и знаменателя. Этапы решения дробно-рациональных неравенств можно описать так:
.Решение дробно-рациональных неравенствХочется сразу предостеречь вас от самой распространенной ошибки: умножения обеих частей неравенства на общий знаменатель. Если при разных значениях х знаменатель может менять знак, то избавляться от него нельзя. Почему? Потому что при умножении обеих частей неравенства на положительное число знак неравенства не меняется, а на отрицательное — меняется на обратный. Поэтому, решая такое неравенство, вы должны учитывать знак не только числителя, но и знаменателя. Этапы решения дробно-рациональных неравенств можно описать так:- 1) перенести все слагаемые в левую часть неравенства;2) привести левую часть к наименьшему общему знаменателю;3) найти корни числителя и знаменателя полученной дроби; проверить, есть ли среди них кратные;4) решить неравенство методом интервалов с учетом кратных корней.
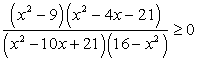 Решение.Данное неравенство равносильно системе:
Решение.Данное неравенство равносильно системе: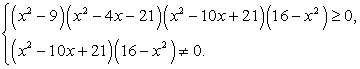 Приведем первое неравенство системы к виду, стандартному для решения методом интервалов:
Приведем первое неравенство системы к виду, стандартному для решения методом интервалов: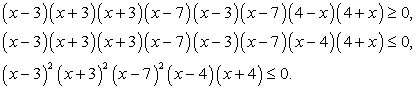 Построим разбиение числовой прямой на промежутки, учитывая второе неравенство системы, то есть, что х ≠
3, х ≠
7, х ≠
± 4, и расставим знаки по правилу чередования:
Построим разбиение числовой прямой на промежутки, учитывая второе неравенство системы, то есть, что х ≠
3, х ≠
7, х ≠
± 4, и расставим знаки по правилу чередования: Решение неравенства:
Решение неравенства: 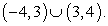 Ответ:
Ответ: 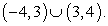 Пример 7.Решить неравенство:
Пример 7.Решить неравенство: 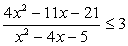 .Решение.Выполним последовательно пункты приведенной «инструкции»:
.Решение.Выполним последовательно пункты приведенной «инструкции»: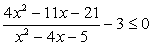 .
.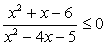 .
.- x2 + х - 6 = 0, x1 = -3, x2 = 2; x2 - 4х - 5 = 0, x1 = -1, x2 = 5.Теперь можно разложить числитель и знаменатель на множители:
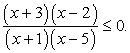 Видим, что в каждой найденной точке меняет знак ровно один из множителей, то есть меняет знак и вся дробь.
Видим, что в каждой найденной точке меняет знак ровно один из множителей, то есть меняет знак и вся дробь. - При х = 0 дробь принимает положительное значение. Расставим знаки на интервалах:).
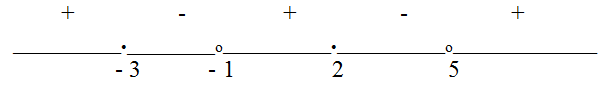
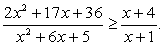 Решение.Выполним тождественные преобразования:
Решение.Выполним тождественные преобразования: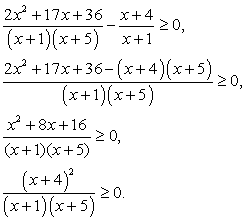 Корень числителя (х = -4)-кратный, так как при этом значении х ни один множитель не меняет знак. Корни знаменателя: х = -5 и х = -1. При х = 0 дробь положительна. Знаки на интервалах:
Корень числителя (х = -4)-кратный, так как при этом значении х ни один множитель не меняет знак. Корни знаменателя: х = -5 и х = -1. При х = 0 дробь положительна. Знаки на интервалах: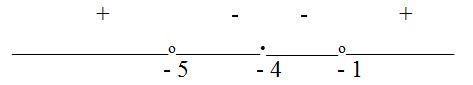 Заметим, что неравенство нестрогое, поэтому точка -4 входит в ответ.Ответ: (- ?; -5) U (-1; ?), x = -4.Комментарий. Напомним, что несколько неравенств образуют систему
Заметим, что неравенство нестрогое, поэтому точка -4 входит в ответ.Ответ: (- ?; -5) U (-1; ?), x = -4.Комментарий. Напомним, что несколько неравенств образуют систему , если поставлена задача отыскания всех тех значений переменной, при которых справедливо каждое из рассматриваемых неравенств. Для решения системы неравенств, таким образом, необходимо решить каждое из неравенств системы, а затем найти пересечение этих решений.Пример 9.Решим систему неравенств:
, если поставлена задача отыскания всех тех значений переменной, при которых справедливо каждое из рассматриваемых неравенств. Для решения системы неравенств, таким образом, необходимо решить каждое из неравенств системы, а затем найти пересечение этих решений.Пример 9.Решим систему неравенств: 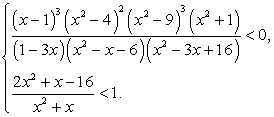 Решение.Решим каждое из неравенств системы.Решение первого неравенства:
Решение.Решим каждое из неравенств системы.Решение первого неравенства: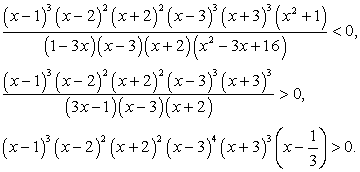
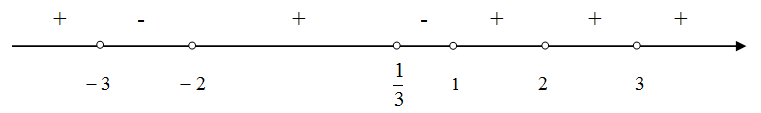
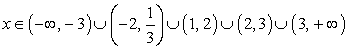 .Решение второго неравенства:
.Решение второго неравенства: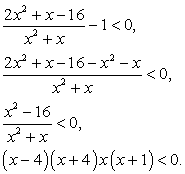 .
. Теперь найдем пересечение решений неравенств. Для этого на одной числовой прямой изобразим оба решения, отмечая их штриховкой разного наклона. Искомым пересечением решений, ясно, будут промежутки двойной штриховки:
Теперь найдем пересечение решений неравенств. Для этого на одной числовой прямой изобразим оба решения, отмечая их штриховкой разного наклона. Искомым пересечением решений, ясно, будут промежутки двойной штриховки: Решение системы неравенств:
Решение системы неравенств: 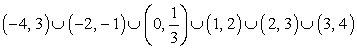 .Ответ:
.Ответ: 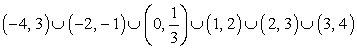 .Пример 10.Решим двойное неравенство:
.Пример 10.Решим двойное неравенство: 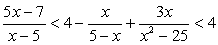 .Решение.Понятно, что речь идет о решении системы неравенств:
.Решение.Понятно, что речь идет о решении системы неравенств: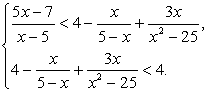 Решим каждое из неравенств системы.Решение первого неравенства:
Решим каждое из неравенств системы.Решение первого неравенства: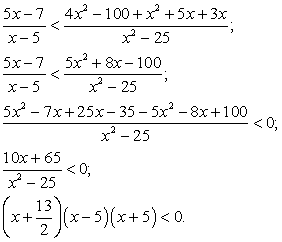

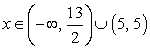 Решение второго неравенства:
Решение второго неравенства: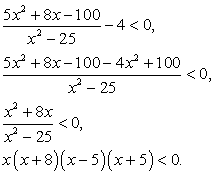
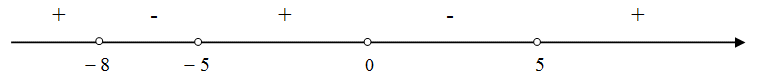 x ϵ
(-8, -5) U (0,5).Найдем пересечение решений неравенств:
x ϵ
(-8, -5) U (0,5).Найдем пересечение решений неравенств: Таким образом, решение системы, то есть решение данного двойного неравенства:
Таким образом, решение системы, то есть решение данного двойного неравенства: 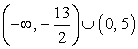 Ответ:
Ответ: 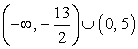 Далее рассмотрим примеры решения еще нескольких рациональных неравенств.Пример 11.Решить неравенство:
Далее рассмотрим примеры решения еще нескольких рациональных неравенств.Пример 11.Решить неравенство: 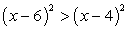 .Решение.Перенесем все слагаемые в левую часть и разложим ее на множители, используя формулу разности квадратов:(х - 6 + х - 4)(х - 6 - х + 4) >
0, (2x - 10)(-2) >
0.Левая часть неравенства равна 0 при х = 5 и меняет знак в этой точке. При х = 0 (-10)(-2) > 0, поэтому знаки на координатной прямой распределяются следующим образом:
.Решение.Перенесем все слагаемые в левую часть и разложим ее на множители, используя формулу разности квадратов:(х - 6 + х - 4)(х - 6 - х + 4) >
0, (2x - 10)(-2) >
0.Левая часть неравенства равна 0 при х = 5 и меняет знак в этой точке. При х = 0 (-10)(-2) > 0, поэтому знаки на координатной прямой распределяются следующим образом: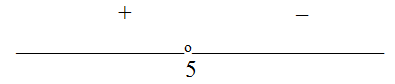 Следовательно, решением неравенства является интервал (-?; 5).Ответ: (-?; 5).Пример 12.Решить неравенство: (x2 - 6х + 8)(x2 - 11х + 28) <
0.Решение.После разложения на множители получаем: (х - 2)(х - 4)2 (х - 7) <
0.х = 4 — кратный корень, потому что (x - 4)2 >
0 и при x <
4, и при x >
4. Поэтому на интервалах, разделенных точкой 4, левая часть неравенства будет иметь одинаковые знаки, а точки 2 и 7 разделяют интервалы с разными знаками левой части. При х = 0 левая часть неравенства положительна, следовательно, знаки распределяются так:
Следовательно, решением неравенства является интервал (-?; 5).Ответ: (-?; 5).Пример 12.Решить неравенство: (x2 - 6х + 8)(x2 - 11х + 28) <
0.Решение.После разложения на множители получаем: (х - 2)(х - 4)2 (х - 7) <
0.х = 4 — кратный корень, потому что (x - 4)2 >
0 и при x <
4, и при x >
4. Поэтому на интервалах, разделенных точкой 4, левая часть неравенства будет иметь одинаковые знаки, а точки 2 и 7 разделяют интервалы с разными знаками левой части. При х = 0 левая часть неравенства положительна, следовательно, знаки распределяются так: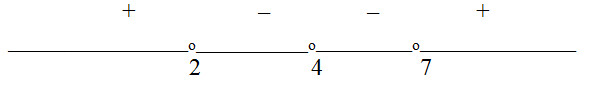 Ответ: (2; 4) U (4; 7).Пример 13.Решить неравенство:
Ответ: (2; 4) U (4; 7).Пример 13.Решить неравенство: 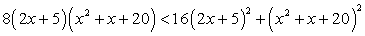 Решение.Перенесем все слагаемые в правую часть и прочтем неравенство «справа налево»:
Решение.Перенесем все слагаемые в правую часть и прочтем неравенство «справа налево»: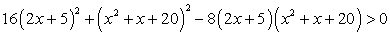 .Теперь заметим, что в левой части полученного неравенства стоит полный квадрат:
.Теперь заметим, что в левой части полученного неравенства стоит полный квадрат: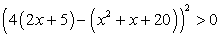 .Значит, неравенство будет верным при любом значении х, кроме тех, при которых его левая часть равна нулю, то есть кроме корней уравнения 4(2x + 5) - (x2 + x + 20) = 0. Решим это уравнение: x2 - 7х = 0, x1 = 0, x2 = 7. Следовательно, решение неравенства можно записать в виде: х ϵ
0, х ϵ
7, или
.Значит, неравенство будет верным при любом значении х, кроме тех, при которых его левая часть равна нулю, то есть кроме корней уравнения 4(2x + 5) - (x2 + x + 20) = 0. Решим это уравнение: x2 - 7х = 0, x1 = 0, x2 = 7. Следовательно, решение неравенства можно записать в виде: х ϵ
0, х ϵ
7, или 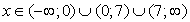 .Ответ:
.Ответ: 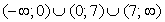 .Комментарий. Если для решения неравенства используется замена переменной, то важно не сделать раньше времени обратную замену. Сначала нужно полностью решить неравенство для вспомогательного неизвестного, найти его возможные значения (записав их не в интервальной форме, а в виде одного или нескольких неравенств), и только после этого подставить в эти неравенства выражение для вспомогательного неизвестного.Пример 14.Решить неравенство: Решение.Сделаем замену t = x2 - 7x + 17 и решим неравенство:
.Комментарий. Если для решения неравенства используется замена переменной, то важно не сделать раньше времени обратную замену. Сначала нужно полностью решить неравенство для вспомогательного неизвестного, найти его возможные значения (записав их не в интервальной форме, а в виде одного или нескольких неравенств), и только после этого подставить в эти неравенства выражение для вспомогательного неизвестного.Пример 14.Решить неравенство: Решение.Сделаем замену t = x2 - 7x + 17 и решим неравенство: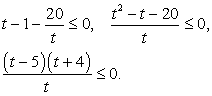 Его решение можно записать так:
Его решение можно записать так: 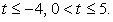 После обратной замены получим:
После обратной замены получим: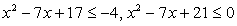 .Дискриминант квадратного трехчлена, стоящего в левой части, отрицателен, следовательно, левая часть неравенства не может изменить знак, то есть сохраняет постоянный знак при любом значении х. Поскольку при х = 0 она отрицательна, то неравенство решений не имеет.
.Дискриминант квадратного трехчлена, стоящего в левой части, отрицателен, следовательно, левая часть неравенства не может изменить знак, то есть сохраняет постоянный знак при любом значении х. Поскольку при х = 0 она отрицательна, то неравенство решений не имеет.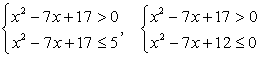 .Первое неравенство верно всегда, решение второго:
.Первое неравенство верно всегда, решение второго: 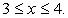 Оно и будет окончательным ответом.Ответ: [3; 4].Пример 15.Решить неравенство: (x2 - 3x + 2)(x2 - 9x + 20) <
180.Решение.Разложим на множители оба квадратных трехчлена: (x - 1)(x - 2)(x - 4)(x - 5) <
180, и перемножим их в другом порядке (первый с последним и второй с третьим):(x2 - 6x + 5)(x2 - 6x + 8) <
180.Теперь можно сделать замену: t = x2 - 6x + 5, тогда:t (t + 3) <
180, t2 + 3t - 180 <
0, (t + 15)(t - 12) <
0, -15 <
t <
12.Обратная замена:
Оно и будет окончательным ответом.Ответ: [3; 4].Пример 15.Решить неравенство: (x2 - 3x + 2)(x2 - 9x + 20) <
180.Решение.Разложим на множители оба квадратных трехчлена: (x - 1)(x - 2)(x - 4)(x - 5) <
180, и перемножим их в другом порядке (первый с последним и второй с третьим):(x2 - 6x + 5)(x2 - 6x + 8) <
180.Теперь можно сделать замену: t = x2 - 6x + 5, тогда:t (t + 3) <
180, t2 + 3t - 180 <
0, (t + 15)(t - 12) <
0, -15 <
t <
12.Обратная замена: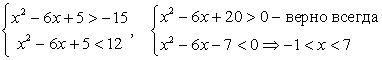 .Ответ: (-1; 7).Пример 16.Решить уравнение: x2 - 6x + 6 + |x - 6| = 0.Решение.Рассмотрим две возможности.Случай 1. x - 6 ≥
0, то есть х ≥
6. Тогда |x - 6| = x - 6, и уравнение принимает вид:x2 - 6x + 6 + x - 6 = 0, x2 - 5х = 0, x1 = 5, x2 = 0.Видим, что оба корня не соответствуют условию, поставленному на знак подмодульного выражения, следовательно, являются посторонними.Случай 2. x - 6 <
0, x <
6; x2 - 6x + 6 - x + 6 = 0, x2 - 7x + 12 = 0, x1 = 3, x2 = 4 - оба корня соответствуют поставленному условию.Ответ: х = 3, х = 4.Комментарий. Аналогично решаются модульные неравенства
.Ответ: (-1; 7).Пример 16.Решить уравнение: x2 - 6x + 6 + |x - 6| = 0.Решение.Рассмотрим две возможности.Случай 1. x - 6 ≥
0, то есть х ≥
6. Тогда |x - 6| = x - 6, и уравнение принимает вид:x2 - 6x + 6 + x - 6 = 0, x2 - 5х = 0, x1 = 5, x2 = 0.Видим, что оба корня не соответствуют условию, поставленному на знак подмодульного выражения, следовательно, являются посторонними.Случай 2. x - 6 <
0, x <
6; x2 - 6x + 6 - x + 6 = 0, x2 - 7x + 12 = 0, x1 = 3, x2 = 4 - оба корня соответствуют поставленному условию.Ответ: х = 3, х = 4.Комментарий. Аналогично решаются модульные неравенства этого типа, но если в уравнении достаточно проверить полученные корни на соответствие условию, задающему знак подмодульного выражения, то решением неравенства является объединение решений двух систем, состоящих из условия на знак подмодульного выражения и неравенства, полученного из исходного после раскрытия модуля.Пример 17.Решить неравенство:
этого типа, но если в уравнении достаточно проверить полученные корни на соответствие условию, задающему знак подмодульного выражения, то решением неравенства является объединение решений двух систем, состоящих из условия на знак подмодульного выражения и неравенства, полученного из исходного после раскрытия модуля.Пример 17.Решить неравенство: 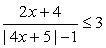 .Случай 1. Пусть 4х + 5 ≥
0, тогда нужно решить систему неравенств:
.Случай 1. Пусть 4х + 5 ≥
0, тогда нужно решить систему неравенств: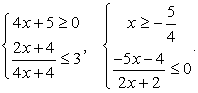 .Решая второе неравенство методом интервалов, получим:
.Решая второе неравенство методом интервалов, получим: 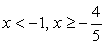 С учетом решения первого неравенства
С учетом решения первого неравенства 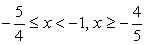 .Случай 2.
.Случай 2. 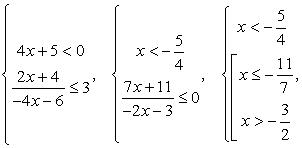 и окончательно
и окончательно 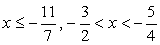 .Объединяя решения обеих систем, находим окончательный ответ.Ответ:
.Объединяя решения обеих систем, находим окончательный ответ.Ответ: 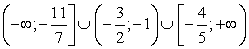 Пример 18.Решить неравенство | |2x - 3| - 7| >
6.Решение.Из неравенства |a| >
b (при b >
0) следует, что a >
b или a <
-b. Рассмотрим эти случаи отдельно:Вспомним, что неравенство |a| <
b выполняется, если -b <
a <
b. Соответственно: 1 <
2x - 3 <
1, 2 <
2x <
4, 1 <
x <
2.Окончательным ответом будет объединение полученных решений.Ответ: (- ?; - 5) U (1; 2) U (8; + ?).Пример 19.Решить неравенство |x + 5| + |2x - 3| <
10.Решение.Корни подмодульных выражений: х = -5 и х = 1,5. Расставим знаки этих выражений на полученных интервалах:
Пример 18.Решить неравенство | |2x - 3| - 7| >
6.Решение.Из неравенства |a| >
b (при b >
0) следует, что a >
b или a <
-b. Рассмотрим эти случаи отдельно:Вспомним, что неравенство |a| <
b выполняется, если -b <
a <
b. Соответственно: 1 <
2x - 3 <
1, 2 <
2x <
4, 1 <
x <
2.Окончательным ответом будет объединение полученных решений.Ответ: (- ?; - 5) U (1; 2) U (8; + ?).Пример 19.Решить неравенство |x + 5| + |2x - 3| <
10.Решение.Корни подмодульных выражений: х = -5 и х = 1,5. Расставим знаки этих выражений на полученных интервалах: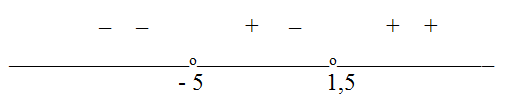 Последовательно решим три системы неравенств.Объединим найденные решения:
Последовательно решим три системы неравенств.Объединим найденные решения: 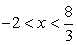 . Видеолекция «Рациональные неравенства»:
. Видеолекция «Рациональные неравенства»: 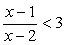 ;
;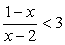 .
.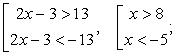
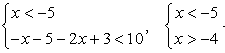 — интервалы не пересекаются, решений нет.
— интервалы не пересекаются, решений нет.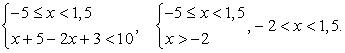 .
.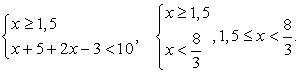 .
.
