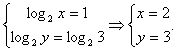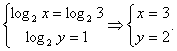Системы уравнений
 , если они имеют общее решение. Решением системы двух уравнений
, если они имеют общее решение. Решением системы двух уравнений называется пара чисел (x0; y0), которая каждое уравнение системы обращает в тождество
называется пара чисел (x0; y0), которая каждое уравнение системы обращает в тождество . Решить систему – значит найти все ее решения.Далее рассмотрим на примерах несколько способов решения систем.
. Решить систему – значит найти все ее решения.Далее рассмотрим на примерах несколько способов решения систем.- Способ подстановки.Решим систему уравнений:
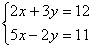 Способ подстановки заключается в следующем:
Способ подстановки заключается в следующем:- 1) выражаем одно неизвестное через другое, воспользовавшись одним из заданных уравнений. Обычно выбирают то уравнение, где это делается проще. В данном случае нам все равно, какое из заданных уравнений использовать для нашей цели. Возьмем, например, первое уравнение системы, и выразим x через y:
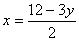 .2) подставим во второе уравнение системы вместо x полученное равенство:
.2) подставим во второе уравнение системы вместо x полученное равенство: 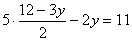 .
.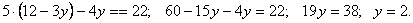 Подставим найденное значение
Подставим найденное значение 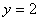 в равенство, выражающее x, получим:
в равенство, выражающее x, получим: 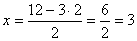 .Таким образом, нами найдена пара значений
.Таким образом, нами найдена пара значений 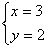 , которая является решением заданной системы. Осталось сделать проверку.Проверка:
, которая является решением заданной системы. Осталось сделать проверку.Проверка: 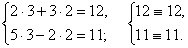
- Способ уравнивания коэффициентов при неизвестных состоит в том, что исходную систему приводят к такой эквивалентной системе, где коэффициенты при x или y были одинаковы. Покажем, как это делается, на данном примере.Решим систему:
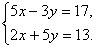
- 1) Для приравнивания коэффициентов, например при y надо найти НОК(3; 5)=15, где 3 и 5 —коэффициенты при y в уравнениях системы. Затем разделить 15 на 3 — коэффициент при y в первом уравнении, получим 5. Делим 15 на 5 — коэффициент при — во втором уравнении, получаем 3. Следовательно, первое уравнение системы умножаем на 5. а второе на 3:
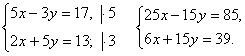 2) Так как коэффициенты при y имеют противоположные знаки, складываем почленно уравнения системы:
2) Так как коэффициенты при y имеют противоположные знаки, складываем почленно уравнения системы: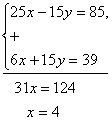 3) Для нахождения соответствующего значения y подставим значение x в любое исходное уравнение системы (обычно подставляют в то уравнение системы, где отыскание значения y проще). В исходной системе уравнения одинаковы по сложности, поэтому подставим значение x = 4 во второе уравнение, чтобы не делать лишней операции деления на -1:
3) Для нахождения соответствующего значения y подставим значение x в любое исходное уравнение системы (обычно подставляют в то уравнение системы, где отыскание значения y проще). В исходной системе уравнения одинаковы по сложности, поэтому подставим значение x = 4 во второе уравнение, чтобы не делать лишней операции деления на -1: 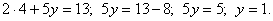
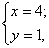 которая является решением заданной системы.
которая является решением заданной системы.
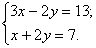 Складывая почленно уравнения заданной системы, получим:
Складывая почленно уравнения заданной системы, получим: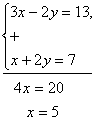 .Подставив вместо x значение 5 во второе уравнение исходной системы, находим соответствующее значение y:
.Подставив вместо x значение 5 во второе уравнение исходной системы, находим соответствующее значение y: 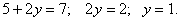 Таким образом, решением системы является
Таким образом, решением системы является 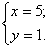 Пример 1.Решим систему уравнений:
Пример 1.Решим систему уравнений: 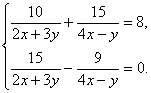 Решение.Положим
Решение.Положим 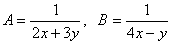 . Тогда придем к системе уравнений:
. Тогда придем к системе уравнений: 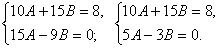 Эту систему решим методом уравнивания коэффициентов. Для этого умножим второе уравнение системы на -2 и сложим с первым уравнением:
Эту систему решим методом уравнивания коэффициентов. Для этого умножим второе уравнение системы на -2 и сложим с первым уравнением: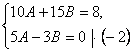
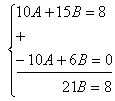 Отсюда получаем, что
Отсюда получаем, что 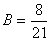 , тогда
, тогда 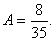 Следовательно, имеем систему уравнений:
Следовательно, имеем систему уравнений: 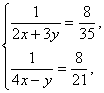 т.е.
т.е. 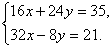 Полученную систему будем решать способом уравнивания коэффициентов. Здесь умножим второе уравнение системы на 3 и сложим с первым уравнением, получим:
Полученную систему будем решать способом уравнивания коэффициентов. Здесь умножим второе уравнение системы на 3 и сложим с первым уравнением, получим: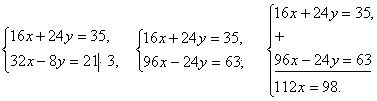 Получаем, что
Получаем, что 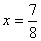 . Подставим найденное значение переменной x в одно из уравнений системы, найдем значение y. Получим ответ:
. Подставим найденное значение переменной x в одно из уравнений системы, найдем значение y. Получим ответ: 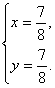 При решении систем тригонометрических уравнений
При решении систем тригонометрических уравнений последние сводят либо к одному уравнению с одним неизвестным, либо к системе уравнений относительно аргументов или функций этих аргументов.Рассмотрим лишь некоторые типы тригонометрических уравнений и наиболее употребительные методы их решения.Решим систему:
последние сводят либо к одному уравнению с одним неизвестным, либо к системе уравнений относительно аргументов или функций этих аргументов.Рассмотрим лишь некоторые типы тригонометрических уравнений и наиболее употребительные методы их решения.Решим систему: 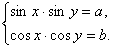 Складывая и вычитая уравнения системы согласно формулам преобразования произведения в сумму функции sin ?, получаем равносильную систему:
Складывая и вычитая уравнения системы согласно формулам преобразования произведения в сумму функции sin ?, получаем равносильную систему: 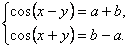 Полученная система имеет решение в том случае, когда выполняются условия
Полученная система имеет решение в том случае, когда выполняются условия 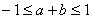 и
и 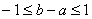 . А поскольку обе системы равносильны, то и исходная система имеет решения только при указанных условиях. Если эти условия выполнены, то
. А поскольку обе системы равносильны, то и исходная система имеет решения только при указанных условиях. Если эти условия выполнены, то 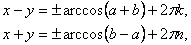 (*), где k и n – любые целые числа, а знаки выбираются произвольно.Пусть
(*), где k и n – любые целые числа, а знаки выбираются произвольно.Пусть 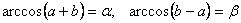 .Таким образом, формулы (*) определяют четыре серии решений:
.Таким образом, формулы (*) определяют четыре серии решений: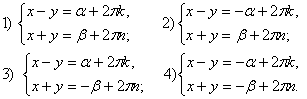 Решая эти системы, находим:
Решая эти системы, находим: Аналогично решается система:
Аналогично решается система: 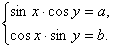 Пример 2.Решить систему:
Пример 2.Решить систему: 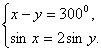 Решение.Сначала в первом уравнении системы перейдем от градусной меры к радианной:
Решение.Сначала в первом уравнении системы перейдем от градусной меры к радианной: 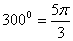 . Далее из первого уравнения системы выражаем y:
. Далее из первого уравнения системы выражаем y: 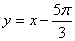 . Тогда второе уравнение примет вид:
. Тогда второе уравнение примет вид: 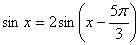 (**).Упростим правую часть полученного уравнения:
(**).Упростим правую часть полученного уравнения: 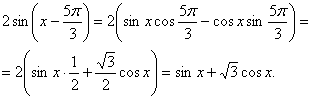 Таким образом, уравнение (**) примет вид
Таким образом, уравнение (**) примет вид 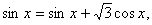 откуда получаем, что
откуда получаем, что 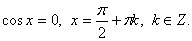 Так как
Так как 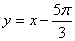 , то подставив значение
, то подставив значение 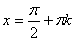 , получим:
, получим: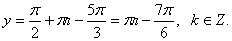 Ответ:
Ответ: 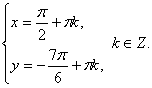 Пример 3.Решить систему:
Пример 3.Решить систему: 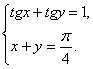 Решение.Область определения системы:
Решение.Область определения системы: 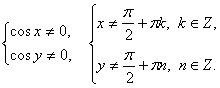 Применяя способ подстановки, получаем:
Применяя способ подстановки, получаем: 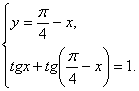 (***) Далее решаем второе уравнение системы, имеем:
(***) Далее решаем второе уравнение системы, имеем: 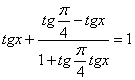 . В результате упрощений получаем:
. В результате упрощений получаем: 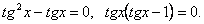 Теперь систему (***) заменим двумя системами:
Теперь систему (***) заменим двумя системами: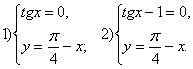 Решим каждую систему.Решение первой системы:
Решим каждую систему.Решение первой системы: 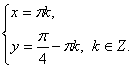 Решение второй системы:
Решение второй системы: 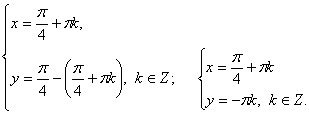 Пример 4.Решить систему уравнений:
Пример 4.Решить систему уравнений: 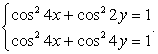 Решение.Вычтем первое уравнение из второго и применим формулу
Решение.Вычтем первое уравнение из второго и применим формулу 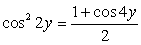 .
.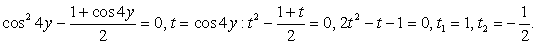 Случай 1: cos 4y = 1, тогда из второго уравнения
Случай 1: cos 4y = 1, тогда из второго уравнения 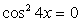 , то есть cos 4x = 0. Получена система двух простейших уравнений:
, то есть cos 4x = 0. Получена система двух простейших уравнений: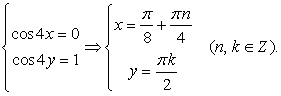 Случай 2:
Случай 2: 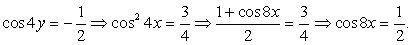 Решая полученную систему простейших уравнений, находим вторую группу корней:
Решая полученную систему простейших уравнений, находим вторую группу корней: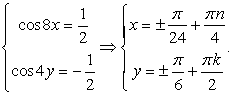 Еще раз напомним, что решение каждого уравнения системы содержит свой целочисленный параметр (решением будет каждая пара чисел, заданная полученными формулами, в которых мы можем задавать n и k любые целые значения, не обязательно одинаковые).Ответ:
Еще раз напомним, что решение каждого уравнения системы содержит свой целочисленный параметр (решением будет каждая пара чисел, заданная полученными формулами, в которых мы можем задавать n и k любые целые значения, не обязательно одинаковые).Ответ: 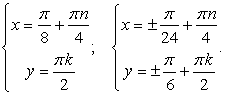 Комментарий. При решении показательно-логарифмических систем
Комментарий. При решении показательно-логарифмических систем применяются как обычные методы решения систем (подстановка, замена переменных), так и приемы решения соответствующих уравнений. Если в системе присутствуют логарифмы, не забудьте об ограничениях на допустимые значения неизвестных. Если получившиеся неравенства трудны для решения (например, неравенства с двумя переменными), можно ограничиться подстановкой в них найденных решений.Пример 5.Решить систему уравнений:
применяются как обычные методы решения систем (подстановка, замена переменных), так и приемы решения соответствующих уравнений. Если в системе присутствуют логарифмы, не забудьте об ограничениях на допустимые значения неизвестных. Если получившиеся неравенства трудны для решения (например, неравенства с двумя переменными), можно ограничиться подстановкой в них найденных решений.Пример 5.Решить систему уравнений: 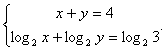 Решение.ОДЗ: x >
0, y >
0.Из первого уравнения можно сделать подстановку:
Решение.ОДЗ: x >
0, y >
0.Из первого уравнения можно сделать подстановку: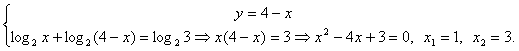 Находим соответствующие значения у: у1 = 4 – 1 = 3, у2 = 4 – 3 = 1. Все найденные решения входят в ОДЗ.Ответ: (1; 3), (3; 1).Пример 6.Решить систему уравнений
Находим соответствующие значения у: у1 = 4 – 1 = 3, у2 = 4 – 3 = 1. Все найденные решения входят в ОДЗ.Ответ: (1; 3), (3; 1).Пример 6.Решить систему уравнений 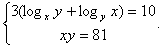 Решение.ОДЗ: x >
0, y >
0, x ≠
1, y ≠
1.Пусть
Решение.ОДЗ: x >
0, y >
0, x ≠
1, y ≠
1.Пусть 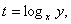 тогда
тогда 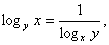 и из первого уравнения получаем:
и из первого уравнения получаем: 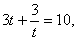 3t2 – 10t + 3 = 0, t1 = 3, t2 =
3t2 – 10t + 3 = 0, t1 = 3, t2 =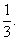 Случай 1.
Случай 1. 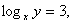 следовательно, у = х3. Подставим во второе уравнение: х4 = 81, с учетом ОДЗ х = 3, у = 33 = 27.Случай 2.
следовательно, у = х3. Подставим во второе уравнение: х4 = 81, с учетом ОДЗ х = 3, у = 33 = 27.Случай 2. 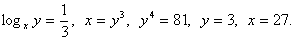 Ответ: (3; 27), (27; 3).Пример 7.Решить систему уравнений
Ответ: (3; 27), (27; 3).Пример 7.Решить систему уравнений 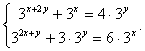 Решение.Сделаем замену:
Решение.Сделаем замену: 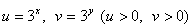 и получим систему
и получим систему 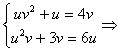
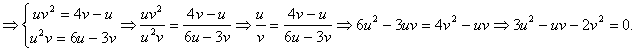 Получено однородное уравнение. Разделим обе части на
Получено однородное уравнение. Разделим обе части на 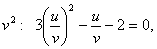
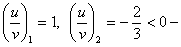 постороннее решение, так это отношение может быть только положительным.Итак,
постороннее решение, так это отношение может быть только положительным.Итак, 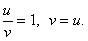 Подставим этот результат в первое уравнение системы для u и v:
Подставим этот результат в первое уравнение системы для u и v: 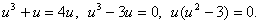 Единственный положительный корень этого уравнения –
Единственный положительный корень этого уравнения – 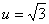 . Тогда
. Тогда 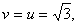 и после обратной замены получаем:
и после обратной замены получаем: 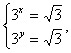 следовательно,
следовательно, 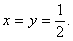 Ответ: (Ѕ; Ѕ).Пример 8.Решить систему уравнений
Ответ: (Ѕ; Ѕ).Пример 8.Решить систему уравнений 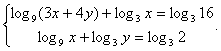 Решение.ОДЗ: x >
0, y >
0.Перейдем во всех логарифмах к основанию 3:
Решение.ОДЗ: x >
0, y >
0.Перейдем во всех логарифмах к основанию 3: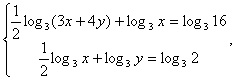
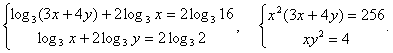 Разделим левую и правую части первого уравнения на соответствующие части второго:
Разделим левую и правую части первого уравнения на соответствующие части второго: 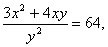
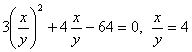 (второе решение отрицательно и является посторонним, так как х и у одного знака, следовательно, их отношение положительно).Получена подстановка: х = 4у. Тогда из второго уравнения последней системы 4у3 = 1, у = 1, х = 4.Ответ: (4; 1).Пример 9.Решить систему уравнений
(второе решение отрицательно и является посторонним, так как х и у одного знака, следовательно, их отношение положительно).Получена подстановка: х = 4у. Тогда из второго уравнения последней системы 4у3 = 1, у = 1, х = 4.Ответ: (4; 1).Пример 9.Решить систему уравнений 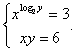 Решение.ОДЗ: x >
0, y >
0.При выполнении этих условий прологарифмируем обе части каждого уравнения по основанию 2:
Решение.ОДЗ: x >
0, y >
0.При выполнении этих условий прологарифмируем обе части каждого уравнения по основанию 2: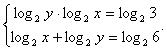 Представим
Представим 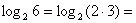
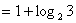 и сделаем замену:
и сделаем замену: 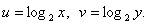 Для новых неизвестных решим систему:
Для новых неизвестных решим систему: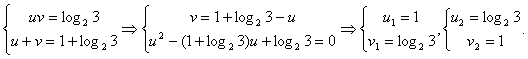 (Заметим, что корни квадратного уравнения для и легко можно найти по теореме Виета
(Заметим, что корни квадратного уравнения для и легко можно найти по теореме Виета ). Обратная замена:Ответ: (2; 3), (3; 2).Пример 10.Для решения (х, у) системы уравнений
). Обратная замена:Ответ: (2; 3), (3; 2).Пример 10.Для решения (х, у) системы уравнений 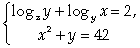 найти х2 + у2.Решение.ОДЗ:
найти х2 + у2.Решение.ОДЗ: 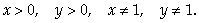 Сделаем в первом уравнении замену
Сделаем в первом уравнении замену 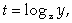 тогда
тогда 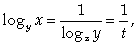 и первое уравнение примет вид:
и первое уравнение примет вид: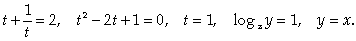 Подставим у = х во второе уравнение:
Подставим у = х во второе уравнение: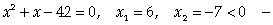 посторонний корень. Следовательно, х2 + у2 = 36 + 36 = 72 (ответ 3).Ответ: 3. Видеолекция «Системы уравнений»:
посторонний корень. Следовательно, х2 + у2 = 36 + 36 = 72 (ответ 3).Ответ: 3. Видеолекция «Системы уравнений»: