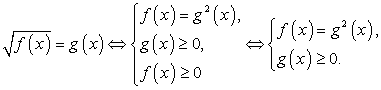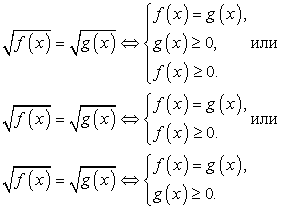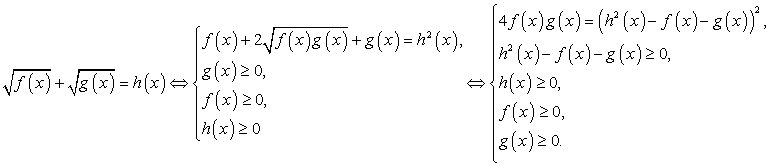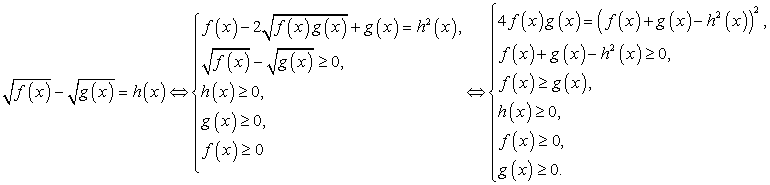Иррациональные уравнения
 и неравенств
и неравенств — возведение в квадрат. Тем не менее, советуем вам пользоваться им как можно реже, ибо он обладает существенными недостатками: во-первых, возводя в квадрат обе части уравнения, вы расширяете область допустимых значений неизвестного, что может привести к появлению посторонних корней; во-вторых, часто в результате этой операции получается уравнение с громоздкими коэффициентами, работать с которыми затруднительно (особенно если на экзамене не разрешается пользоваться калькулятором). Наконец, главный недостаток этого приема — увеличение вдвое степени уравнения. Возведя обе части в квадрат, вы можете избавиться от иррациональностей, но получить рациональное уравнение степени выше второй, способы решения которого в общем виде вам неизвестны или вообще не существуют.Если возводить в квадрат все-таки приходится, нужно внимательно следить за тем, чтобы не включить в ответ посторонние корни. В частности, если уравнение имеет вид
— возведение в квадрат. Тем не менее, советуем вам пользоваться им как можно реже, ибо он обладает существенными недостатками: во-первых, возводя в квадрат обе части уравнения, вы расширяете область допустимых значений неизвестного, что может привести к появлению посторонних корней; во-вторых, часто в результате этой операции получается уравнение с громоздкими коэффициентами, работать с которыми затруднительно (особенно если на экзамене не разрешается пользоваться калькулятором). Наконец, главный недостаток этого приема — увеличение вдвое степени уравнения. Возведя обе части в квадрат, вы можете избавиться от иррациональностей, но получить рациональное уравнение степени выше второй, способы решения которого в общем виде вам неизвестны или вообще не существуют.Если возводить в квадрат все-таки приходится, нужно внимательно следить за тем, чтобы не включить в ответ посторонние корни. В частности, если уравнение имеет вид 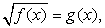 то для корней должно выполняться условие
то для корней должно выполняться условие 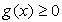 (при этом
(при этом 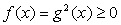 , и условие
, и условие 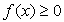 отдельно ставить не требуется). Еще один способ обнаружить посторонние корни — проверка всех найденных корней подстановкой их в первоначальное уравнение.Пример 1.Решить уравнение:
отдельно ставить не требуется). Еще один способ обнаружить посторонние корни — проверка всех найденных корней подстановкой их в первоначальное уравнение.Пример 1.Решить уравнение: 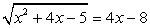 .РешениеКорни должны удовлетворять условию 4х - 8 ≥
0, то есть х ≥
2. Возведем обе части в квадрат:
.РешениеКорни должны удовлетворять условию 4х - 8 ≥
0, то есть х ≥
2. Возведем обе части в квадрат: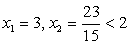 — посторонний корень.Ответ: х = 3.Пример 2.
— посторонний корень.Ответ: х = 3.Пример 2.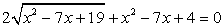 .Поскольку неизвестное входит в подкоренное выражение и в рациональную часть уравнения в виде одной и той же комбинации (x2 - 7х), можно сделать замену:
.Поскольку неизвестное входит в подкоренное выражение и в рациональную часть уравнения в виде одной и той же комбинации (x2 - 7х), можно сделать замену: 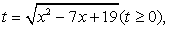 , тогда x2 - 7х = t2 - 19, и t определяется из уравнения: 2t + t2 - 19 + 4 = 0, t2 + 2t — 15 = 0, t1 = 3, t2 = -5 <
0 — не соответствует условию на знак t.Обратная замена:
, тогда x2 - 7х = t2 - 19, и t определяется из уравнения: 2t + t2 - 19 + 4 = 0, t2 + 2t — 15 = 0, t1 = 3, t2 = -5 <
0 — не соответствует условию на знак t.Обратная замена: 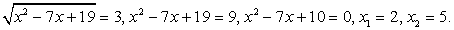 Ответ: х = 2, х = 5.Комментарий. Замена переменной очень полезна при решении иррациональных уравнений. Часто с ее помощью удается избежать необходимости возведения в квадрат.Пример 3.Решить уравнение:
Ответ: х = 2, х = 5.Комментарий. Замена переменной очень полезна при решении иррациональных уравнений. Часто с ее помощью удается избежать необходимости возведения в квадрат.Пример 3.Решить уравнение: 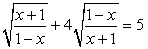 .РешениеПодкоренные выражения — взаимно обратные дроби, поэтому замена
.РешениеПодкоренные выражения — взаимно обратные дроби, поэтому замена 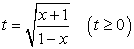 приводит к уравнению:
приводит к уравнению: 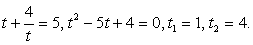 Случай 1.
Случай 1. 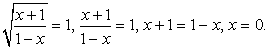 Случай 2.
Случай 2. 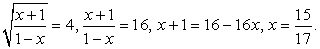 Ответ:
Ответ: 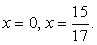 Комментарий. Следует обратить внимание на то, что в некоторых заданиях нет необходимости в проверке корней или задании каких-либо ограничений: значения х определяются из условия, что корень принимает некоторое неотрицательное значение.Пример 4.Решить уравнение:
Комментарий. Следует обратить внимание на то, что в некоторых заданиях нет необходимости в проверке корней или задании каких-либо ограничений: значения х определяются из условия, что корень принимает некоторое неотрицательное значение.Пример 4.Решить уравнение: 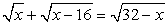 .РешениеПерепишем уравнение в виде:
.РешениеПерепишем уравнение в виде: 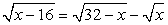 и возведем обе части в квадрат, не задавая никаких ограничений: проще будет в конце работы проверить получившиеся корни:
и возведем обе части в квадрат, не задавая никаких ограничений: проще будет в конце работы проверить получившиеся корни: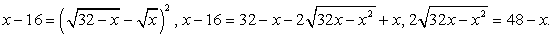 Еще раз возведем в квадрат обе части полученного равенства:
Еще раз возведем в квадрат обе части полученного равенства: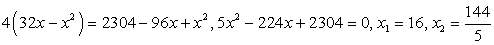 .Проверка.
.Проверка.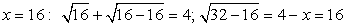 — корень уравнения.
— корень уравнения.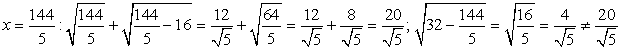 —
— 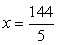 — не корень уравнения.Ответ: х = 16.Пример 5.Решить уравнение:
— не корень уравнения.Ответ: х = 16.Пример 5.Решить уравнение: 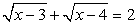 .В этом уравнении замена
.В этом уравнении замена 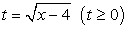 поможет ограничиться только одним возведением в квадрат:
поможет ограничиться только одним возведением в квадрат: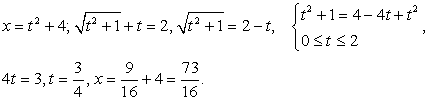 Ответ:
Ответ: 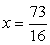 .Пример 6.
.Пример 6.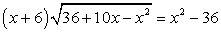 .РешениеОДЗ задается условием:
.РешениеОДЗ задается условием: 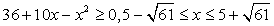 . Запишем уравнение в виде:
. Запишем уравнение в виде: 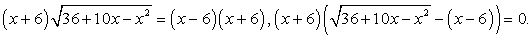
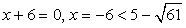 — посторонний корень.
— посторонний корень.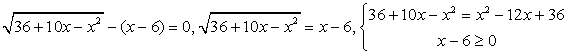 ,
,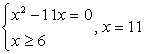 (корень первого уравнения х = 0 не удовлетворяет второму условию). Итак, единственный корень исходного уравнения — х = 11.Ответ: х = 11.Рассмотренные примеры решаются просто, но в более сложных случаях обязательное соблюдение условия равносильности преобразований может привести к серьезным техническим трудностям, сделать решение слишком ветвящимся и громоздким. Поэтому, не будем строго запрещать применение любых неравносильных преобразований. Все ли они одинаково опасны? Понятно, что более опасны неравносильные преобразования, приводящие к потере корней. В большинстве случаев потерянные корни отыскать весьма трудно (заметим также, что малоопытный решающий, а абитуриент часто именно таков, может вовсе не заметить факта потери корня и не будет пытаться его отыскать, хотя это, может быть, и получилось бы).Итак, на не равносильные преобразования, приводящие к потере корней, мы накладываем строгий и категорический запрет. При решении уравнений, таким образом, мы не будем применять деление обеих частей уравнения на выражение, обращающееся в ноль в области определения уравнения, и не будем применять преобразования, приводящие к сужению области определения уравнения.Что же касается неравносильных преобразований, приводящих к появлению посторонних корней, то такие преобразования вполне допустимы. Но при этом, обязательным заключительным этапом решения должна быть проверка всех найденных в итоге корней. Заметим, что тактика проверки зависит непосредственно от класса уравнений (рациональные, иррациональные, логарифмические и т.д.), ибо в каждом случае свои причины появления посторонних корней. В этой связи, тактика проверки конечно должна быть гибкой, но можно пользоваться и универсальным приемом: подстановка всех корней итогового уравнения в исходное с последующим вычислением или «прикидкой».Пример 7.Решим уравнение:
(корень первого уравнения х = 0 не удовлетворяет второму условию). Итак, единственный корень исходного уравнения — х = 11.Ответ: х = 11.Рассмотренные примеры решаются просто, но в более сложных случаях обязательное соблюдение условия равносильности преобразований может привести к серьезным техническим трудностям, сделать решение слишком ветвящимся и громоздким. Поэтому, не будем строго запрещать применение любых неравносильных преобразований. Все ли они одинаково опасны? Понятно, что более опасны неравносильные преобразования, приводящие к потере корней. В большинстве случаев потерянные корни отыскать весьма трудно (заметим также, что малоопытный решающий, а абитуриент часто именно таков, может вовсе не заметить факта потери корня и не будет пытаться его отыскать, хотя это, может быть, и получилось бы).Итак, на не равносильные преобразования, приводящие к потере корней, мы накладываем строгий и категорический запрет. При решении уравнений, таким образом, мы не будем применять деление обеих частей уравнения на выражение, обращающееся в ноль в области определения уравнения, и не будем применять преобразования, приводящие к сужению области определения уравнения.Что же касается неравносильных преобразований, приводящих к появлению посторонних корней, то такие преобразования вполне допустимы. Но при этом, обязательным заключительным этапом решения должна быть проверка всех найденных в итоге корней. Заметим, что тактика проверки зависит непосредственно от класса уравнений (рациональные, иррациональные, логарифмические и т.д.), ибо в каждом случае свои причины появления посторонних корней. В этой связи, тактика проверки конечно должна быть гибкой, но можно пользоваться и универсальным приемом: подстановка всех корней итогового уравнения в исходное с последующим вычислением или «прикидкой».Пример 7.Решим уравнение: 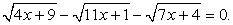 Комментарий. При решении этого уравнения будем придерживаться стратегии, допускающей неравносильные преобразования при обязательной проверке корней. Решая уравнения вида
Комментарий. При решении этого уравнения будем придерживаться стратегии, допускающей неравносильные преобразования при обязательной проверке корней. Решая уравнения вида 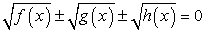 , следует перед возведением в квадрат уединить один из корней, перенеся его в правую часть уравнения. Уединить можно любой из корней, и в большинстве случаев, все равно какой. Но иногда уединение определенного корня приводит к более простому решению, чем уединение других. Поэтому всегда следует анализировать ситуацию в указанном аспекте.РешениеВ нашем уравнение сумма коэффициентов при х в первом и третьем подкоренных выражениях равна коэффициенту при х во втором подкоренном выражении. Поэтому уединить целесообразно именно корень
, следует перед возведением в квадрат уединить один из корней, перенеся его в правую часть уравнения. Уединить можно любой из корней, и в большинстве случаев, все равно какой. Но иногда уединение определенного корня приводит к более простому решению, чем уединение других. Поэтому всегда следует анализировать ситуацию в указанном аспекте.РешениеВ нашем уравнение сумма коэффициентов при х в первом и третьем подкоренных выражениях равна коэффициенту при х во втором подкоренном выражении. Поэтому уединить целесообразно именно корень 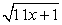 . Полученное после возведения в квадрат уравнение будет содержать х только под корнем. Если бы мы уединяли любой из других корней, то после возведения в квадрат получали бы уравнения, содержащие х и под корнем, и вне корня, что менее удобно для последующего решения.Итак, имеем:
. Полученное после возведения в квадрат уравнение будет содержать х только под корнем. Если бы мы уединяли любой из других корней, то после возведения в квадрат получали бы уравнения, содержащие х и под корнем, и вне корня, что менее удобно для последующего решения.Итак, имеем: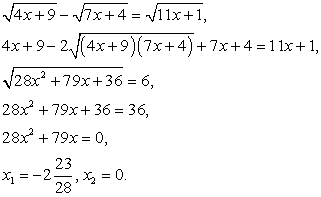 Комментарий. При решении иррационального уравнения мы осуществляем так называемую рационализацию уравнения
Комментарий. При решении иррационального уравнения мы осуществляем так называемую рационализацию уравнения , т.е. избавляемся от радикалов (корней). Но, избавляясь от корней, мы избавляемся и от ограничений на подкоренные выражения:
, т.е. избавляемся от радикалов (корней). Но, избавляясь от корней, мы избавляемся и от ограничений на подкоренные выражения: 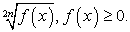 Иными словами, происходит расширение области определения уравнения. Это причина появления посторонних корней. Поэтому все корни итогового уравнения, полученного в ходе решение, следует проверить на принадлежность области определения исходного уравнения. В нашем случае область определения исходного уравнения задается системой:
Иными словами, происходит расширение области определения уравнения. Это причина появления посторонних корней. Поэтому все корни итогового уравнения, полученного в ходе решение, следует проверить на принадлежность области определения исходного уравнения. В нашем случае область определения исходного уравнения задается системой: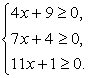 Решив эту систему, получаем область определения уравнения:
Решив эту систему, получаем область определения уравнения: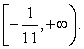 Очевидно, что
Очевидно, что 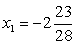 — посторонний корень, появившийся в процессе решения из-за применения неравносильных преобразований, приведших к расширению области определения уравнения, а x2 = 0 —– принадлежит области определения уравнения и является его корнем (что легко проверить непосредственной подстановкой).Ответ: х = 0.Комментарий. Но единственная ли причина появления посторонних корней при решении иррациональных уравнений с радикалами четной степени — расширение области определения исходного уравнения? Не кроется ли в возведении обеих частей уравнения в четную степень еще одна, менее очевидная, но не менее опасная в смысле ошибки, причина появления посторонних корней?Пример 8.
— посторонний корень, появившийся в процессе решения из-за применения неравносильных преобразований, приведших к расширению области определения уравнения, а x2 = 0 —– принадлежит области определения уравнения и является его корнем (что легко проверить непосредственной подстановкой).Ответ: х = 0.Комментарий. Но единственная ли причина появления посторонних корней при решении иррациональных уравнений с радикалами четной степени — расширение области определения исходного уравнения? Не кроется ли в возведении обеих частей уравнения в четную степень еще одна, менее очевидная, но не менее опасная в смысле ошибки, причина появления посторонних корней?Пример 8.- а) Решим уравнение:
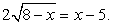 При решении этого уравнения будем придерживаться стратегии, допускающей неравносильные преобразования, т.е. возведем обе части уравнения в квадрат, решим полученное рациональное уравнение и сделаем проверку корней.Итак,
При решении этого уравнения будем придерживаться стратегии, допускающей неравносильные преобразования, т.е. возведем обе части уравнения в квадрат, решим полученное рациональное уравнение и сделаем проверку корней.Итак, 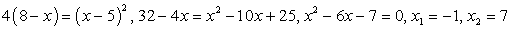 .Проверим, удовлетворяют ли эти корни исходному уравнению.Пусть х = -1, тогда левая часть исходного уравнения равна -6. Таким образом, х = -1 — посторонний для исходного уравнения корень, появившийся в процессе решения из-за применения неравносильных преобразований. Пусть теперь, х = 7. Тогда исходное уравнение превращается в верное числовое равенство. Исходное уравнение, таким образом, имеет единственный корень х = 7.б) Решим теперь уравнение
.Проверим, удовлетворяют ли эти корни исходному уравнению.Пусть х = -1, тогда левая часть исходного уравнения равна -6. Таким образом, х = -1 — посторонний для исходного уравнения корень, появившийся в процессе решения из-за применения неравносильных преобразований. Пусть теперь, х = 7. Тогда исходное уравнение превращается в верное числовое равенство. Исходное уравнение, таким образом, имеет единственный корень х = 7.б) Решим теперь уравнение 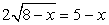 (его чрезвычайно, малое отличие от предыдущего уравнения очевидно).Поступая так же, как в случае «а», получаем:
(его чрезвычайно, малое отличие от предыдущего уравнения очевидно).Поступая так же, как в случае «а», получаем: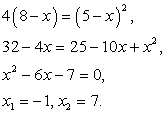
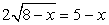 . Пусть х = -1, тогда исходное уравнение превращается в верное числовое равенство. Пусть, далее, х = 7. Тогда левая часть исходного уравнения равна -2. Таким образом, х = 7 — посторонний для исходного уравнения корень.В процессе решения следствием уравнений «а», «б» является одно и тоже уравнение
. Пусть х = -1, тогда исходное уравнение превращается в верное числовое равенство. Пусть, далее, х = 7. Тогда левая часть исходного уравнения равна -2. Таким образом, х = 7 — посторонний для исходного уравнения корень.В процессе решения следствием уравнений «а», «б» является одно и тоже уравнение 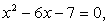 имеющее два корня: x1 = -1 и x2 = 7. Корень x1 = -1 — есть корень уравнения «б», но посторонний для уравнения «а»; корень x2 = 7 — наоборот, корень уравнения «а», посторонний для уравнения «б».В каждом из случаев «а» и «б» корни, оказавшиеся посторонними, принадлежат области определения данного уравнения. Значит, расширение области определения исходного уравнения — не единственная причина появления посторонних корней. В чем же дело? Заметим, что и в случае «а», и в случае «б» при подстановке в исходное уравнение корень, оказывающийся посторонним, приводит к ситуации: левая и правая части уравнения равны по абсолютной величине, но противоположны по знаку. Это не случайно. Уравнение
имеющее два корня: x1 = -1 и x2 = 7. Корень x1 = -1 — есть корень уравнения «б», но посторонний для уравнения «а»; корень x2 = 7 — наоборот, корень уравнения «а», посторонний для уравнения «б».В каждом из случаев «а» и «б» корни, оказавшиеся посторонними, принадлежат области определения данного уравнения. Значит, расширение области определения исходного уравнения — не единственная причина появления посторонних корней. В чем же дело? Заметим, что и в случае «а», и в случае «б» при подстановке в исходное уравнение корень, оказывающийся посторонним, приводит к ситуации: левая и правая части уравнения равны по абсолютной величине, но противоположны по знаку. Это не случайно. Уравнение 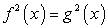 является следствием не только уравнения
является следствием не только уравнения 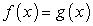 , но и следствием уравнения
, но и следствием уравнения 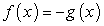 . Какие следует сделать из этого выводы?Во-первых, поскольку появление посторонних корней при решении иррациональных уравнений, содержащих радикалы четной степени может быть и не связано с областью определения исходного уравнения, то и проверка корней не может осуществляться только по области определения, или условиям ее задающим.Во-вторых, проверка корней иррационального уравнения, должна учитывать обе причины появления посторонних корней; универсальный прием, как уже говорилось, состоит в непосредственной подстановке в исходное уравнение, но могут быть реализованы и другие подходы.
. Какие следует сделать из этого выводы?Во-первых, поскольку появление посторонних корней при решении иррациональных уравнений, содержащих радикалы четной степени может быть и не связано с областью определения исходного уравнения, то и проверка корней не может осуществляться только по области определения, или условиям ее задающим.Во-вторых, проверка корней иррационального уравнения, должна учитывать обе причины появления посторонних корней; универсальный прием, как уже говорилось, состоит в непосредственной подстановке в исходное уравнение, но могут быть реализованы и другие подходы.- Сначала отсечь те корни, которые не принадлежат области определения исходного уравнения, а оставшиеся проверить непосредственной подстановкой во все уравнения левая и правая части которых возводились в квадрат в процессе решения.
- Опять же исключить все корни, не принадлежащие области определения, а затем проанализировать все случаи возведения в квадрат обеих частей уравнения, выделить те случаи, где было нарушено условие равносильности:
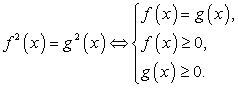 Далее только в эти уравнения подставить корни итогового уравнения, принадлежащие области определения исходного уравнения.
Далее только в эти уравнения подставить корни итогового уравнения, принадлежащие области определения исходного уравнения. - Если решать иррациональные уравнения, применяя только равносильные преобразования, то в каждом случае возведения в квадрат следует предусматривать условие равносильности, сформулированное выше, и изначально следует зафиксировать условия, задающие область определения исходного уравнения.
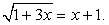 РешениеВозведя обе части уравнения в квадрат, получаем 1 + 3х = x2 + 2х + 1, т.е. уравнение x2 – х = 0. Его корни x1 = 0 и x2 = 1. Подставляя каждый из найденных корней в исходное уравнение, убеждаемся, что оба они являются его корнями.Пример 10.Решим уравнение:
РешениеВозведя обе части уравнения в квадрат, получаем 1 + 3х = x2 + 2х + 1, т.е. уравнение x2 – х = 0. Его корни x1 = 0 и x2 = 1. Подставляя каждый из найденных корней в исходное уравнение, убеждаемся, что оба они являются его корнями.Пример 10.Решим уравнение: 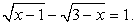 РешениеУединим радикалы:
РешениеУединим радикалы: 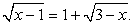 Возведем обе части уравнения в квадрат (дважды):
Возведем обе части уравнения в квадрат (дважды):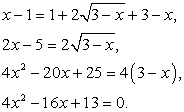 Корни последнего уравнения:
Корни последнего уравнения: 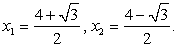 Далее следует провести проверку корней. Область определения исходного уравнения задается условиями
Далее следует провести проверку корней. Область определения исходного уравнения задается условиями 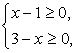 т.е. 1 ≤
x ≤
3. Как нетрудно проверить, полагая
т.е. 1 ≤
x ≤
3. Как нетрудно проверить, полагая 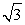 приближенно равным 1,7, что оба корня x1 и x2 принадлежат области определения исходного уравнения. Значит, если среди x1 и x2 есть посторонний корень, то причина его появления связана с нарушением условия равносильного возведения обеих частей уравнения в квадрат. Ясно, также, что первое из проделанных в данном решении возведений в квадрат — равносильное преобразование, поэтому если и появились посторонние корни, то при возведении в квадрат обеих частей уравнения
приближенно равным 1,7, что оба корня x1 и x2 принадлежат области определения исходного уравнения. Значит, если среди x1 и x2 есть посторонний корень, то причина его появления связана с нарушением условия равносильного возведения обеих частей уравнения в квадрат. Ясно, также, что первое из проделанных в данном решении возведений в квадрат — равносильное преобразование, поэтому если и появились посторонние корни, то при возведении в квадрат обеих частей уравнения 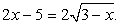 Непосредственной подстановкой именно в это уравнение проверим наши корни x1 и x2.Итак, пусть
Непосредственной подстановкой именно в это уравнение проверим наши корни x1 и x2.Итак, пусть 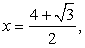 тогда:
тогда: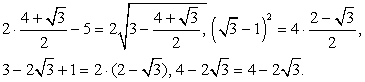 Мы пришли к верному числовому равенству. Значит
Мы пришли к верному числовому равенству. Значит 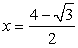 — корень данного уравнения.Пусть теперь
— корень данного уравнения.Пусть теперь 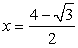 .Тогда
.Тогда 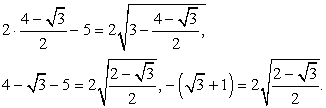 Ясно, что левая часть уравнения отрицательна, а правая положительна. Поэтому
Ясно, что левая часть уравнения отрицательна, а правая положительна. Поэтому 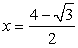 — посторонний корень.Пример 11.Решим уравнение:
— посторонний корень.Пример 11.Решим уравнение: 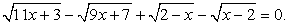 Распределим радикалы следующим образом:
Распределим радикалы следующим образом: 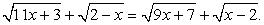 Возведем обе части уравнения в квадрат и приведем подобные слагаемые:
Возведем обе части уравнения в квадрат и приведем подобные слагаемые: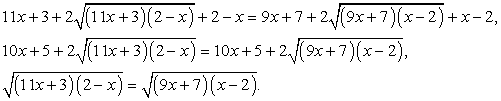 Возведем обе части полученного уравнения в квадрат, раскроем скобки и приведем подобные слагаемые:
Возведем обе части полученного уравнения в квадрат, раскроем скобки и приведем подобные слагаемые: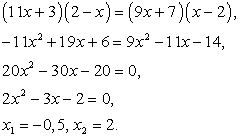 Проведем проверку корней. Сразу замечаем, что корень
Проведем проверку корней. Сразу замечаем, что корень 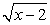 не имеет смысла при x = -0,5. Поэтому единственный возможный корень исходного уравнения — это х = 2, удовлетворяющий всем условиям области определения. Поскольку, возводя обе части уравнения в квадрат, мы всякий раз соблюдали условие равносильности, то х = 2 — единственный корень исходного уравнения.Пример 12.Решим уравнение:
не имеет смысла при x = -0,5. Поэтому единственный возможный корень исходного уравнения — это х = 2, удовлетворяющий всем условиям области определения. Поскольку, возводя обе части уравнения в квадрат, мы всякий раз соблюдали условие равносильности, то х = 2 — единственный корень исходного уравнения.Пример 12.Решим уравнение: 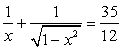 .При решении этого уравнения покажем применение метода введения новой переменной при решении иррациональных уравнений.Возведем обе части уравнения в квадрат:
.При решении этого уравнения покажем применение метода введения новой переменной при решении иррациональных уравнений.Возведем обе части уравнения в квадрат: 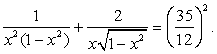 Пусть теперь
Пусть теперь 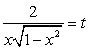 , тогда уравнение можно переписать в виде:
, тогда уравнение можно переписать в виде: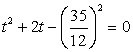 .Это уравнение имеет два корня:
.Это уравнение имеет два корня: 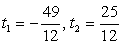 . Таким образом, следствием исходного уравнения является совокупность систем:
. Таким образом, следствием исходного уравнения является совокупность систем: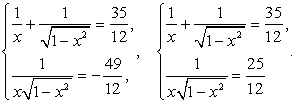 .Решим первую систему совокупности.Обозначим:
.Решим первую систему совокупности.Обозначим: 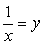 и
и 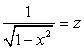 .Тогда имеем:
.Тогда имеем: 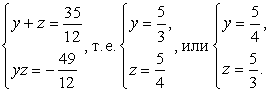 Таким образом,
Таким образом, 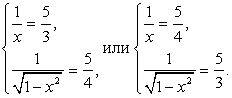 Корни этой совокупности систем:
Корни этой совокупности систем: 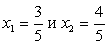 Аналогично, решая вторую систему исходной совокупности, получаем:
Аналогично, решая вторую систему исходной совокупности, получаем: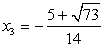 .Пример 13.Решим уравнение:
.Пример 13.Решим уравнение: 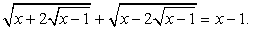 Подкоренные выражения
Подкоренные выражения 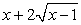 и
и 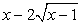 представляют из себя полные квадраты:
представляют из себя полные квадраты: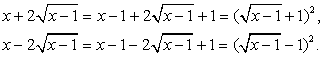 Тогда:
Тогда: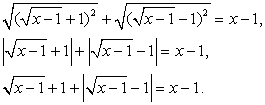 Пусть
Пусть 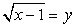 , тогда уравнение можно переписать в виде:
, тогда уравнение можно переписать в виде: 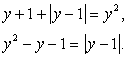 Возведем обе части последнего уравнения в квадрат, затем воспользуемся тождеством
Возведем обе части последнего уравнения в квадрат, затем воспользуемся тождеством 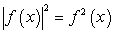 и формулой разности квадратов:
и формулой разности квадратов: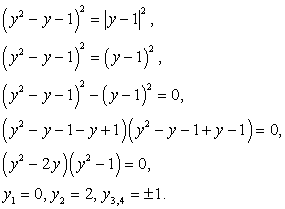 Если у = 0, то
Если у = 0, то 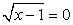 , т.е. х = 1. Если у = 2, то
, т.е. х = 1. Если у = 2, то 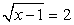 , т.е. х = 5. Если у = 1, то
, т.е. х = 5. Если у = 1, то 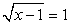 , т.е. х = 2. Если у = -1, то уравнение
, т.е. х = 2. Если у = -1, то уравнение 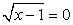 не имеет корней.Непосредственной подстановкой в исходное уравнение всех найденных значений х, приходим к выводу, что только х = 5 является корнем данного уравнения.Рассмотрим далее примеры решения иррациональных уравнений с корнями степени, большей, чем вторая.Пример 14.Решим уравнение:
не имеет корней.Непосредственной подстановкой в исходное уравнение всех найденных значений х, приходим к выводу, что только х = 5 является корнем данного уравнения.Рассмотрим далее примеры решения иррациональных уравнений с корнями степени, большей, чем вторая.Пример 14.Решим уравнение: 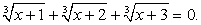 Перераспределим радикалы:
Перераспределим радикалы: 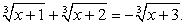 Возведем обе части уравнения в третью степень:
Возведем обе части уравнения в третью степень: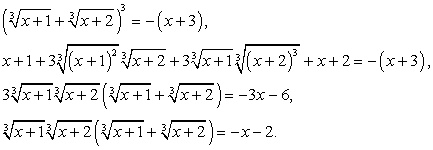 Выражение в скобках, очевидно, есть —
Выражение в скобках, очевидно, есть — 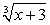 , т.е.:
, т.е.: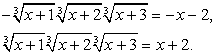 Снова возведем обе части уравнения в третью степень:
Снова возведем обе части уравнения в третью степень: 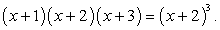 Далее имеем:
Далее имеем: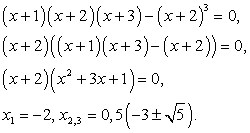 В процессе решения был применен прием, связанный с заменой суммы
В процессе решения был применен прием, связанный с заменой суммы 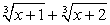 на выражение
на выражение 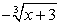 , что могло привести к появлению посторонних корней (такой вывод позволяет сделать определенная искусственность этого приема). Поэтому проверим все найденные корни непосредственной подстановкой в исходное уравнение.Если х = -2, то исходное уравнение обращается в верное числовое равенство.Для подстановки значений
, что могло привести к появлению посторонних корней (такой вывод позволяет сделать определенная искусственность этого приема). Поэтому проверим все найденные корни непосредственной подстановкой в исходное уравнение.Если х = -2, то исходное уравнение обращается в верное числовое равенство.Для подстановки значений 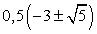 возьмем приближенное значение:
возьмем приближенное значение: 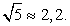 Тогда
Тогда 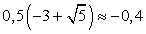 и
и 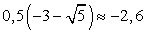 .Если х = -0,4, то:
.Если х = -0,4, то: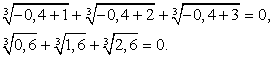 Ясно, что это числовое равенство неверно, поскольку все три значения корней положительны, а сумма положительных чисел не может быть равна 0.Если х = -2,6, то:
Ясно, что это числовое равенство неверно, поскольку все три значения корней положительны, а сумма положительных чисел не может быть равна 0.Если х = -2,6, то: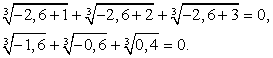 Ясно, что эта сумма не может быть равна 0, т.к. уже
Ясно, что эта сумма не может быть равна 0, т.к. уже 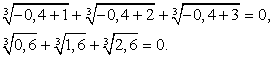 Заметим, что довольно часто, «прикидка» при проверки корней позволяет сделать необходимый вывод на определенном промежуточном этапе вычислений, и доводить их до явного числового равенства или неравенства совсем не обязательно (это снова к вопросу о гибкой тактике проверки корней).Таким образом, х = -2 — единственный корень данного уравнения.Ответ: -2.Комментарий. Запишем в общем виде прием решения, рассмотренный в этом примере:
Заметим, что довольно часто, «прикидка» при проверки корней позволяет сделать необходимый вывод на определенном промежуточном этапе вычислений, и доводить их до явного числового равенства или неравенства совсем не обязательно (это снова к вопросу о гибкой тактике проверки корней).Таким образом, х = -2 — единственный корень данного уравнения.Ответ: -2.Комментарий. Запишем в общем виде прием решения, рассмотренный в этом примере: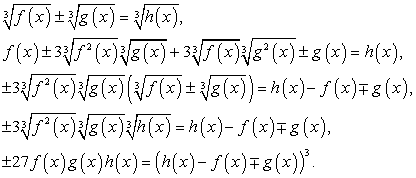 По аналогичной схеме решаются уравнения вида
По аналогичной схеме решаются уравнения вида 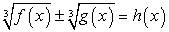 .Большие трудности у абитуриентов вызывают иррациональные уравнения, содержащие радикалы разных степеней. Рассмотрим примеры.Пример 15.
.Большие трудности у абитуриентов вызывают иррациональные уравнения, содержащие радикалы разных степеней. Рассмотрим примеры.Пример 15.- Решим уравнение:
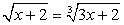 .Это уравнение легко рационализируется возведением обеих его частей в шестую степень:
.Это уравнение легко рационализируется возведением обеих его частей в шестую степень: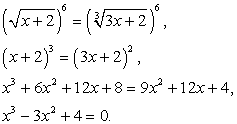 И далее:
И далее: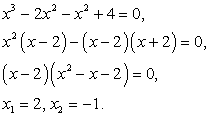 Подстановкой выясняем, что только х = 2 является корнем данного уравнения.
Подстановкой выясняем, что только х = 2 является корнем данного уравнения. - Решим уравнение:
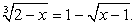 В этом случае возведение обеих частей уравнения в шестую степень уже нецелесообразно. Проведем замену переменных.Пусть
В этом случае возведение обеих частей уравнения в шестую степень уже нецелесообразно. Проведем замену переменных.Пусть 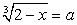 и
и 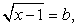 тогда a + b = 1. Возведем в куб первое уравнение системы
тогда a + b = 1. Возведем в куб первое уравнение системы 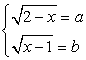 ,и в квадрат второе уравнение этой системы; затем почленно сложим полученные уравнения. В итоге получаем: a3 + b2 = 1.Таким образом, имеем систему уравнений:
,и в квадрат второе уравнение этой системы; затем почленно сложим полученные уравнения. В итоге получаем: a3 + b2 = 1.Таким образом, имеем систему уравнений: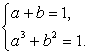 Решая ее, получаем:
Решая ее, получаем: 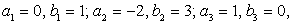 т.е. совокупность систем:
т.е. совокупность систем: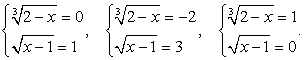 В итоге
В итоге 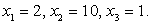 Непосредственная подстановка в исходное уравнение показывает, что среди этих корней нет посторонних.
Непосредственная подстановка в исходное уравнение показывает, что среди этих корней нет посторонних.
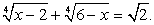 Пусть
Пусть 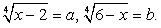 Тогда
Тогда 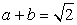 . Возведем в четвертую степень обе части каждого из уравнений системы
. Возведем в четвертую степень обе части каждого из уравнений системы 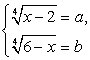 и почленно сложим полученные уравнения. В итоге получаем:
и почленно сложим полученные уравнения. В итоге получаем: 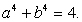 Таким образом, имеем систему уравнений:
Таким образом, имеем систему уравнений: 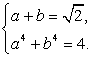 Это симметрическая система уравнений, стандартно решающаяся заменой переменных a + b = y и ab = z.Имеем корни:
Это симметрическая система уравнений, стандартно решающаяся заменой переменных a + b = y и ab = z.Имеем корни: 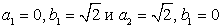 . Отсюда x1 = 2, x2 = 6. Проверка показывает, что это действительно корни данного уравнения.Ответ: x1 = 2, x2 = 6. Видеолекция «Иррациональные уравнения»:
. Отсюда x1 = 2, x2 = 6. Проверка показывает, что это действительно корни данного уравнения.Ответ: x1 = 2, x2 = 6. Видеолекция «Иррациональные уравнения»: