Комбинированные выражения
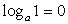 .Комментарий. Логарифм единицы по любому основанию равен нулю. Для того, чтобы убедиться в истинности данной формулы, достаточно вспомнить, что любое число (кроме нуля) в нулевой степени равно единице.
.Комментарий. Логарифм единицы по любому основанию равен нулю. Для того, чтобы убедиться в истинности данной формулы, достаточно вспомнить, что любое число (кроме нуля) в нулевой степени равно единице.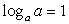 .Комментарий. Логарифм равен единице в случае равенства чисел (выражений) — основания логарифма и выражения, стоящего под логарифмом.
.Комментарий. Логарифм равен единице в случае равенства чисел (выражений) — основания логарифма и выражения, стоящего под логарифмом.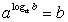 .Комментарий. Представленная формула является одним из вариантов записи определения логарифма.
.Комментарий. Представленная формула является одним из вариантов записи определения логарифма.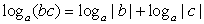 .
.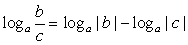 .
.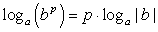 .
.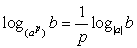 .
.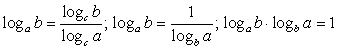 .Комментарий.Данная формула называемая формулой перехода к новому основанию, имеет два важных следствия. Приравняем в формуле
.Комментарий.Данная формула называемая формулой перехода к новому основанию, имеет два важных следствия. Приравняем в формуле 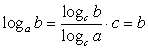 , тогда
, тогда 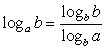 . Рассмотрим числитель полученной дроби. Поставим вопрос: в какую степень следует возвести число b, чтобы получить число b. Ответ — в первую степень, т.е. числитель рассматриваемой дроби равен единице. Таким образом,
. Рассмотрим числитель полученной дроби. Поставим вопрос: в какую степень следует возвести число b, чтобы получить число b. Ответ — в первую степень, т.е. числитель рассматриваемой дроби равен единице. Таким образом, 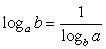 . В ряде задач полезно бывает полученную формулу записать в преобразованном виде:
. В ряде задач полезно бывает полученную формулу записать в преобразованном виде: 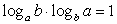 .
.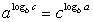 .
.
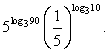 РешениеПредставим
РешениеПредставим 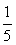 в виде степени числа 5, тогда
в виде степени числа 5, тогда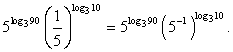 Далее воспользуемся правилом умножения степеней одинаковым основанием (при умножении степеней с одинаковым основанием показатели складываются):
Далее воспользуемся правилом умножения степеней одинаковым основанием (при умножении степеней с одинаковым основанием показатели складываются):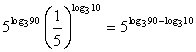 .Преобразуем полученную в процессе решения разность логарифмов (по одному основанию) и применим определение логарифма (зададим вопрос: В какую степень следует возвести основание логарифма 3, чтобы получить число, стоящее под логарифмом — 9?):
.Преобразуем полученную в процессе решения разность логарифмов (по одному основанию) и применим определение логарифма (зададим вопрос: В какую степень следует возвести основание логарифма 3, чтобы получить число, стоящее под логарифмом — 9?): 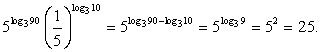 Ответ: 25.Пример 2.Упростить выражение
Ответ: 25.Пример 2.Упростить выражение 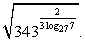 РешениеУпростим показатель степени подкоренного выражения:
РешениеУпростим показатель степени подкоренного выражения: 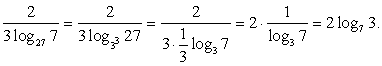 Тогда
Тогда 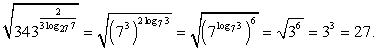 Ответ: 27.Пример 3.Упростить выражение:
Ответ: 27.Пример 3.Упростить выражение: 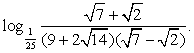 РешениеВначале упростим логарифмируемое выражение. Если Вы уже занимались упрощением алгебраических выражений, то вид первого множителя в знаменателе вызовет предположение, что перед нами полный квадрат. Действительно,
РешениеВначале упростим логарифмируемое выражение. Если Вы уже занимались упрощением алгебраических выражений, то вид первого множителя в знаменателе вызовет предположение, что перед нами полный квадрат. Действительно, 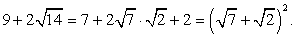 Тогда:
Тогда: 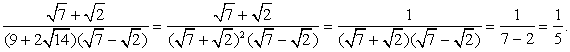 Следовательно,
Следовательно, 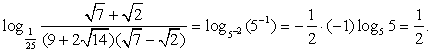 Ответ: 1/2.Пример 4.Найти значение выражения
Ответ: 1/2.Пример 4.Найти значение выражения 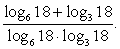 РешениеРазделим на знаменатель каждое слагаемое числителя по отдельности:
РешениеРазделим на знаменатель каждое слагаемое числителя по отдельности: 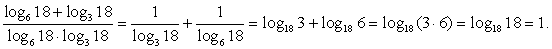 Переходя далее в каждом слагаемом к новому основанию 18, получаем, что:
Переходя далее в каждом слагаемом к новому основанию 18, получаем, что: 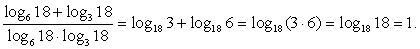 Преобразуем далее сумму логарифмов с одинаковым основанием в логарифм произведения и используем определение логарифма:
Преобразуем далее сумму логарифмов с одинаковым основанием в логарифм произведения и используем определение логарифма: 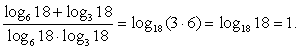 Ответ: 1.Пример 5.Вычислить
Ответ: 1.Пример 5.Вычислить 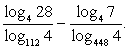 РешениеДля преобразования данного выражения перейдем во всех логарифмах к основанию 4:
РешениеДля преобразования данного выражения перейдем во всех логарифмах к основанию 4: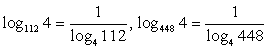 .Тогда выражение принимает вид:
.Тогда выражение принимает вид: 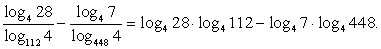 Далее разложим на множители логарифмируемые выражения, выделяя в каждом из них множитель вида 4n:28 = 4*7, 112 = 16*7 = 42*7, 448 = 64*7 = 43*7.Продолжим преобразование выражения, используя свойства логарифмов:
Далее разложим на множители логарифмируемые выражения, выделяя в каждом из них множитель вида 4n:28 = 4*7, 112 = 16*7 = 42*7, 448 = 64*7 = 43*7.Продолжим преобразование выражения, используя свойства логарифмов: 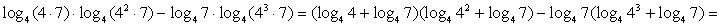
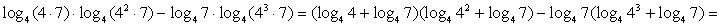
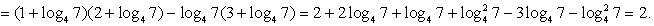 Ответ: 2.Пример 6.Вычислить
Ответ: 2.Пример 6.Вычислить 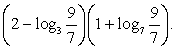 РешениеПредставим числа 2 и 1 в виде:
РешениеПредставим числа 2 и 1 в виде: 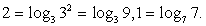 Тогда
Тогда 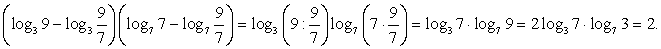 Ответ: 2.Пример 7.Найти
Ответ: 2.Пример 7.Найти 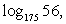 если
если 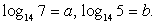 РешениеОбратим внимание на то, что в каждом логарифме (либо в основании, либо в аргументе) присутствует множитель 7. Поэтому перейдем к основанию 7 во всех логарифмах:
РешениеОбратим внимание на то, что в каждом логарифме (либо в основании, либо в аргументе) присутствует множитель 7. Поэтому перейдем к основанию 7 во всех логарифмах: 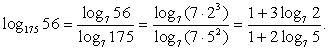 Обратим внимание, что
Обратим внимание, что 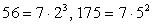 , тогда:Следовательно, для вычисления этого логарифма нужно знать значения и
, тогда:Следовательно, для вычисления этого логарифма нужно знать значения и 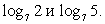 Воспользуемся формулами перехода к новому основанию:
Воспользуемся формулами перехода к новому основанию: 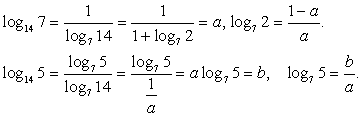 Подставим далее найденные значения в преобразованное исходное выражение:
Подставим далее найденные значения в преобразованное исходное выражение: 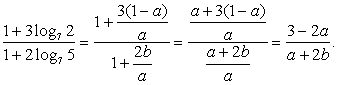 Ответ:
Ответ: 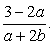 Пример 8.Известно, что
Пример 8.Известно, что 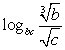 лежит между числами 8 и 13, а
лежит между числами 8 и 13, а 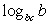 принимает целые значения. Найти количество этих значений.РешениеПерейдем в обоих логарифмах к основанию b.Для этого воспользуемся сначала формулой «логарифм частного»:
принимает целые значения. Найти количество этих значений.РешениеПерейдем в обоих логарифмах к основанию b.Для этого воспользуемся сначала формулой «логарифм частного»: 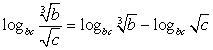 . Обратим далее внимание, что
. Обратим далее внимание, что 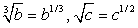 .Получаем, что
.Получаем, что 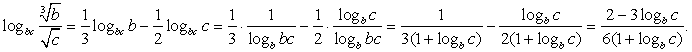 Решим методом интервалов неравенство:
Решим методом интервалов неравенство: 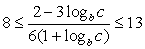 .Для этого перейдем к систем нестрогих неравенств:
.Для этого перейдем к систем нестрогих неравенств: 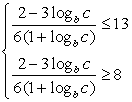 .Рассматривая каждое из записанных неравенств отдельно и впоследствии находя решение как пересечение множеств (решений первого и второго неравенств), получаем:
.Рассматривая каждое из записанных неравенств отдельно и впоследствии находя решение как пересечение множеств (решений первого и второго неравенств), получаем: 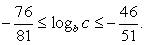 Выполним преобразования полученного двойного неравенства.Прибавим 1 ко всем частям неравенства:
Выполним преобразования полученного двойного неравенства.Прибавим 1 ко всем частям неравенства: 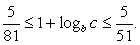 Поскольку
Поскольку 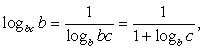 его значения задаются неравенством:
его значения задаются неравенством: 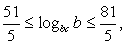 или
или 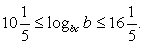 Следовательно,
Следовательно, 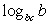 может принимать 6 целых значений – от 11 до 16.Ответ: 6.Комментарий. Далее проработаем выполнение заданий на тождественные преобразования тригонометрических выражений, поскольку они встречаются в ЕГЭ как в качестве отдельных заданий, так и используются для решения тригонометрический уравнений и неравенств, а также комбинированных заданий. Для решения задач на упрощение тригонометрических выражений требуется достаточно хорошо знать правила преобразования алгебраических выражений и тригонометрические формулы (уметь применять их как по одной, так и в комплексе).Основные формулы тригонометрииПеревод градусной меры угла в радианную и обратно.Пусть α — градусная мера угла, β — радианная, тогда справедливы формулы:
может принимать 6 целых значений – от 11 до 16.Ответ: 6.Комментарий. Далее проработаем выполнение заданий на тождественные преобразования тригонометрических выражений, поскольку они встречаются в ЕГЭ как в качестве отдельных заданий, так и используются для решения тригонометрический уравнений и неравенств, а также комбинированных заданий. Для решения задач на упрощение тригонометрических выражений требуется достаточно хорошо знать правила преобразования алгебраических выражений и тригонометрические формулы (уметь применять их как по одной, так и в комплексе).Основные формулы тригонометрииПеревод градусной меры угла в радианную и обратно.Пусть α — градусная мера угла, β — радианная, тогда справедливы формулы: 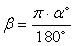 ,
, 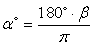 .Формулы зависимости между функциями одного и того же аргумента:Формулы сложения.Формулы двойных и половинных углов.Формулы преобразования суммы в произведение:
.Формулы зависимости между функциями одного и того же аргумента:Формулы сложения.Формулы двойных и половинных углов.Формулы преобразования суммы в произведение:
|
|
|
|
|
|
|
|
φ |
α |
|
|
|
|
|
|
|
|
sin φ |
- sin α |
cos α |
cos α |
sin α |
- sin α |
- cos α |
- cos α |
- sin α |
sin α |
cos φ |
cos α |
sin α |
- sin α |
- cos α |
- cos α |
- sin α |
sin α |
cos α |
cos α |
tg φ |
- tg α |
ctg α |
- ctg α |
- tg α |
tg α |
ctg α |
- ctg α |
- tg α |
tg α |
ctg φ |
- ctg α |
tg α |
- tg α |
- ctg α |
ctg α |
tg α |
- tg α |
- ctg α |
ctg α |
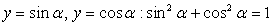 .Так как по условию задачи cosα = 0,3, то cos2α = 0,09. Значит, sin2α + 0,09 = 1, sin2α = 1 – 0,09 = 0,91. Решая уравнение sin2α = 0,91, получаем два случая (
.Так как по условию задачи cosα = 0,3, то cos2α = 0,09. Значит, sin2α + 0,09 = 1, sin2α = 1 – 0,09 = 0,91. Решая уравнение sin2α = 0,91, получаем два случая (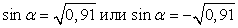 ), из которых, обращая внимание на то, какой четверти принадлежит искомый угол, следует выбрать один. Вспомним, что в первой четверти все тригонометрические функции имеют знак «+». Следовательно,
), из которых, обращая внимание на то, какой четверти принадлежит искомый угол, следует выбрать один. Вспомним, что в первой четверти все тригонометрические функции имеют знак «+». Следовательно, 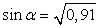 .Ответ:
.Ответ: 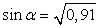 .Пример 10.Вычислите значение tg α, если ctg α = 0,2.РешениеВоспользуемся формулой, связывающей тригонометрические функции y = tg α, y = ctg α : tg α * ctg α = 1. Подставляя заданное в условии значение 0,2, получаем, что tg α * 0,2 = 1, откуда tg α = 5.Ответ: 5.Пример 11.Упростите выражения:
РешениеДанные задания — на применение формул сложения.
.Пример 10.Вычислите значение tg α, если ctg α = 0,2.РешениеВоспользуемся формулой, связывающей тригонометрические функции y = tg α, y = ctg α : tg α * ctg α = 1. Подставляя заданное в условии значение 0,2, получаем, что tg α * 0,2 = 1, откуда tg α = 5.Ответ: 5.Пример 11.Упростите выражения:
РешениеДанные задания — на применение формул сложения.- 1)
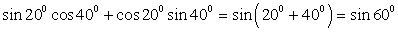 . Обратимся далее к таблице значений тригонометрических функций. Получаем, что
. Обратимся далее к таблице значений тригонометрических функций. Получаем, что 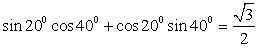 .2)
.2) 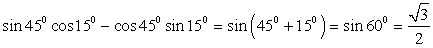 .3) Воспользуемся формулой «косинус суммы», тогда
.3) Воспользуемся формулой «косинус суммы», тогда 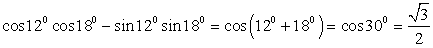 .4)
.4) 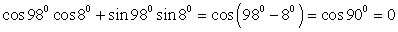 .5) Применим формулу «тангенс суммы», получим
.5) Применим формулу «тангенс суммы», получим 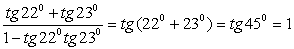 .6)
.6) 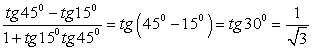 .
.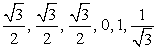 .Пример 12.Вычислите:
Решение
.Пример 12.Вычислите:
Решение- 1) Воспользуемся свойством периодичности функции y = sin x, тогда
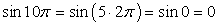 .2) Так как период функции y = tg x равен π, получаем:
.2) Так как период функции y = tg x равен π, получаем: 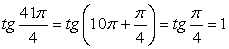 .3) Представим 75º
в виде суммы двух «удобных» слагаемых: 75º
= 45º
+ 30º
. Следовательно,
.3) Представим 75º
в виде суммы двух «удобных» слагаемых: 75º
= 45º
+ 30º
. Следовательно, 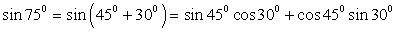 . Обратимся к табличным значениям тригонометрических функций, получим:
. Обратимся к табличным значениям тригонометрических функций, получим: 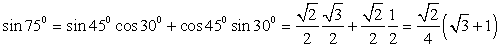 .4)
.4) 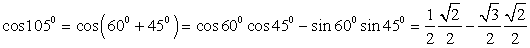 . Окончательно получаем, что
. Окончательно получаем, что 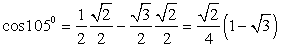 .5) Для вычисления значения cos 15º
представим 15º
как 15º
= 45º
- 30º
(или 15º
= 60º
- 45º
). Тогда
.5) Для вычисления значения cos 15º
представим 15º
как 15º
= 45º
- 30º
(или 15º
= 60º
- 45º
). Тогда 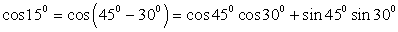 . Обратимся далее к табличным значениям тригонометрических функций. Получаем, что
. Обратимся далее к табличным значениям тригонометрических функций. Получаем, что 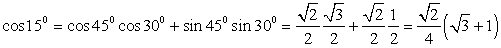 . Cледовательно,
. Cледовательно, 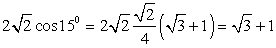 .
.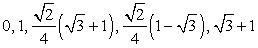 .Отдельную группу заданий этого типа составляют задания на вычисление одних тригонометрических функций по известным другим.Пример 13.Известно, что sin α – cos α = 0,3. Найти:1) sin2α;2) sin4α + cos4α;3) sin6α + cos6α.Решение
.Отдельную группу заданий этого типа составляют задания на вычисление одних тригонометрических функций по известным другим.Пример 13.Известно, что sin α – cos α = 0,3. Найти:1) sin2α;2) sin4α + cos4α;3) sin6α + cos6α.Решение- 1) Возведем в квадрат обе части заданного в условии примера равенства и используем формулу «квадрат разности», получаем, что:sin2α - 2sinα cosα + cos2α = 0,09.Вспомним основное тригонометрическое тождество и применим формулу синуса двойного угла:1 - sin2α = 0,09, откуда:sin2α = 1 - 0,09 = 0,91.2) Воспользуемся полученным результатом для ответа на вопрос 2.Для этого сумму sin4α + cos4α представим в специальном виде:sin4α + cos4α = (sin4α + 2sin2α cos2α + cos4α) - 2sin2α cos2α = (sin2α + cos2α)2 - 1/2 α sin22α = 1 - 1/2 * 0,91 = 0,545.Комментарий. Специальный вид, использованный при решении данного примера, позволяет применить формулу «квадрат суммы» и использовать результат, полученный в пункте 1. При последующих преобразованиях использована формула синуса двойного угла.3) Обратим внимание, что для вычисления значения выражение sin6α + cos6α можно представить в виде суммы кубов.sin6α + cos6α = (sin2α)3 + (cos2α)3 = (sin2α + cos2α)(sin4α - sin2α cos2α + cos4α) = 1 * (0,545 – 1/4 * 0,91) = 0,3175.
- 1) 0,91;2) 0,545;3) 0,3175.
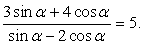 РешениеПроверкой можно убедиться, что при cos α = 0 приведенное равенство неверно. Поэтому следует разделить числитель и знаменатель дроби на cos α (на основании основного свойства дроби):
РешениеПроверкой можно убедиться, что при cos α = 0 приведенное равенство неверно. Поэтому следует разделить числитель и знаменатель дроби на cos α (на основании основного свойства дроби):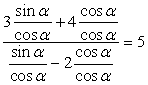 , следовательно,
, следовательно, 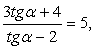 тогда:
тогда: 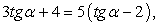 раскрывая скобки, приведем далее подобные слагаемые:3tg α + 4 = 5tg α - 10, 2tg α = 14, получаем, что tg α = 7.Ответ: 7.Пример 15.Вычислить cos α, если cos2α = 3/4 и
раскрывая скобки, приведем далее подобные слагаемые:3tg α + 4 = 5tg α - 10, 2tg α = 14, получаем, что tg α = 7.Ответ: 7.Пример 15.Вычислить cos α, если cos2α = 3/4 и 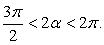 РешениеКак известно,
РешениеКак известно, 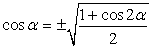 . Выясним, в каких пределах лежит угол α и какой знак при этом имеет его косинус. Преобразуем заданное в условии задачи двойное неравенство. Разделив одновременно все три части двойного неравенства на 2, получим:
. Выясним, в каких пределах лежит угол α и какой знак при этом имеет его косинус. Преобразуем заданное в условии задачи двойное неравенство. Разделив одновременно все три части двойного неравенства на 2, получим: 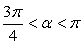 , то есть угол α располагается во второй четверти и, следовательно, cos α<
0.В приведенной выше формуле выберем знак «минус»:
, то есть угол α располагается во второй четверти и, следовательно, cos α<
0.В приведенной выше формуле выберем знак «минус»: 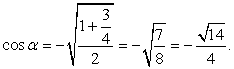 Ответ:
Ответ: 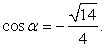 Комментарий. Следующая группа заданий — вычисление значений различных тригонометрических выражений с использованием тригонометрических формул.Пример 16.Найти значение выражения:
Комментарий. Следующая группа заданий — вычисление значений различных тригонометрических выражений с использованием тригонометрических формул.Пример 16.Найти значение выражения: 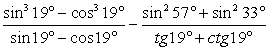 .Выполним упрощение каждой дроби по отдельности.С целью сокращения дроби
.Выполним упрощение каждой дроби по отдельности.С целью сокращения дроби 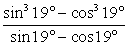 воспользуемся формулой «разность кубов» и получим:
воспользуемся формулой «разность кубов» и получим: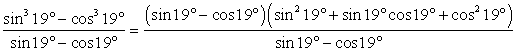 .Рассмотрим далее выражение
.Рассмотрим далее выражение 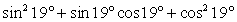 . Нужно заметить, что первое третье слагаемые в сумме дают единицу в силу основного тригонометрического тождества. Таким образом:
. Нужно заметить, что первое третье слагаемые в сумме дают единицу в силу основного тригонометрического тождества. Таким образом: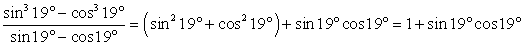 .Обратимся далее к преобразованию второй дроби. Применим одну из формул приведения:
.Обратимся далее к преобразованию второй дроби. Применим одну из формул приведения: 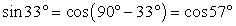 . Поэтому:
. Поэтому: 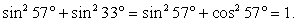 Тогда
Тогда 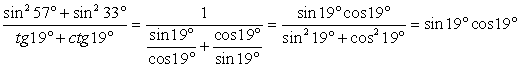 .Окончательно получаем:
.Окончательно получаем: 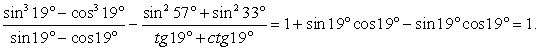 Ответ: 1.Пример 17.Вычислить sin10º
sin30º
sin50º
sin70º
.Используем формулу преобразования произведения тригонометрических функций в сумму: sin10º
sin50º
= 1/2 (cos40º
- cos60º
) = 1/2 cos 40º
- 1/4. Подставим в первоначальное произведение это выражение и учтем, что sin30º
= 1/2, получаем:
Ответ: 1.Пример 17.Вычислить sin10º
sin30º
sin50º
sin70º
.Используем формулу преобразования произведения тригонометрических функций в сумму: sin10º
sin50º
= 1/2 (cos40º
- cos60º
) = 1/2 cos 40º
- 1/4. Подставим в первоначальное произведение это выражение и учтем, что sin30º
= 1/2, получаем: 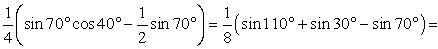
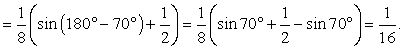 Ответ:
Ответ: 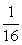 Комментарий. Для выполнения аналогичных заданий необходимо знание не только тригонометрических формул, но и табличных значений тригонометрических функций.Рассмотрим далее примеры упрощения тригонометрических выражений с произвольным аргументом.Пример 18.Упростить выражение:
Комментарий. Для выполнения аналогичных заданий необходимо знание не только тригонометрических формул, но и табличных значений тригонометрических функций.Рассмотрим далее примеры упрощения тригонометрических выражений с произвольным аргументом.Пример 18.Упростить выражение: 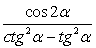 .Так как числитель заданной дроби имеет достаточно простой вид, начнем с упрощения знаменателя. Для этого применим представление
.Так как числитель заданной дроби имеет достаточно простой вид, начнем с упрощения знаменателя. Для этого применим представление 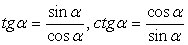 :
: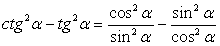 .Приведем полученную разность дробей к общему знаменателю:
.Приведем полученную разность дробей к общему знаменателю: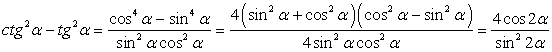 .Следовательно,
.Следовательно, 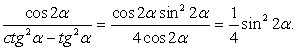 Ответ:
Ответ: 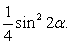 Пример 19.Доказать тождество при
Пример 19.Доказать тождество при 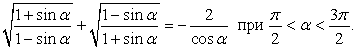 Комментарий. Задания на доказательство тождеств вполне можно воспринимать как задания на упрощение выражений, причем с готовым ответом в виде более простой и компактной части равенства.РешениеВ частности, в данном примере попробуем упростить левую часть, чтобы получить такое же выражение, как справа. Для этого помножим числитель и знаменатель подкоренного выражения на 1 + sin α:
Комментарий. Задания на доказательство тождеств вполне можно воспринимать как задания на упрощение выражений, причем с готовым ответом в виде более простой и компактной части равенства.РешениеВ частности, в данном примере попробуем упростить левую часть, чтобы получить такое же выражение, как справа. Для этого помножим числитель и знаменатель подкоренного выражения на 1 + sin α: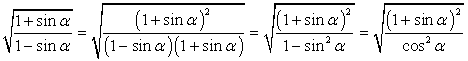 .Вспомнив, что
.Вспомнив, что 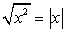 , получаем
, получаем 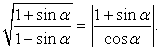 Исследуем далее знак числителя и знаменателя подмодульного выражения:sin α ≥
-1, тогда 1 + sin α ≥
0 поэтому
Исследуем далее знак числителя и знаменателя подмодульного выражения:sin α ≥
-1, тогда 1 + sin α ≥
0 поэтому 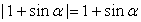 ;при
;при 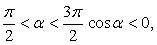 следовательно,
следовательно, 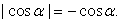 Таким образом:
Таким образом: 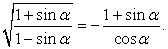 Аналогичным образом преобразуем второе слагаемое левой части:
Аналогичным образом преобразуем второе слагаемое левой части: 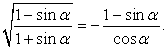 Тогда,
Тогда, 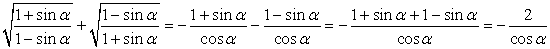 , что и требовалось доказать.Пример 20.Найти значение следующих тригонометрических выражений: sin 2α, cos 2α, tg 2α, если
, что и требовалось доказать.Пример 20.Найти значение следующих тригонометрических выражений: sin 2α, cos 2α, tg 2α, если 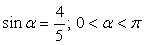 .РешениеВыпишем формулы для вычисления искомых функций:
.РешениеВыпишем формулы для вычисления искомых функций: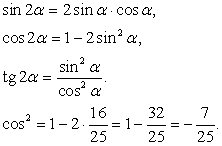 Из основного тригонометрического тождества вычислим:
Из основного тригонометрического тождества вычислим: 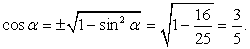 Далее найдем значения искомых выражений:
Далее найдем значения искомых выражений: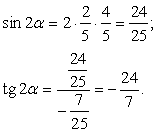 Ответ:
Ответ: 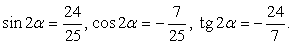 Пример 21.Доказать тождество
Пример 21.Доказать тождество 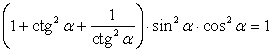 .РешениеПриведем левую часть к 1:
.РешениеПриведем левую часть к 1: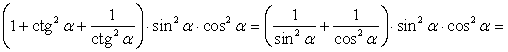
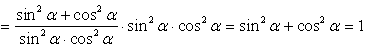 .Тождество доказано.Пример 22.Вычислить значение выражения:
.Тождество доказано.Пример 22.Вычислить значение выражения: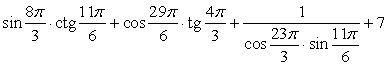 .РешениеОбратим внимание, что
.РешениеОбратим внимание, что 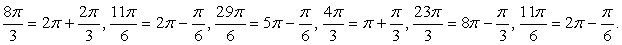 Далее, используя формулы приведения, получим:
Далее, используя формулы приведения, получим: 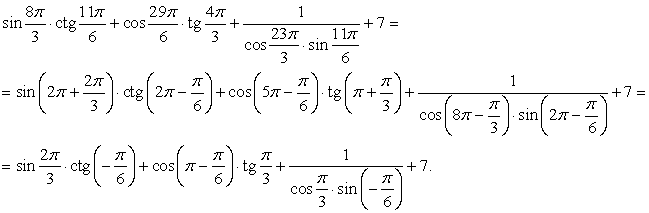 Воспользуемся табличными значениями и свойствами тригонометрических функций:
Воспользуемся табличными значениями и свойствами тригонометрических функций: 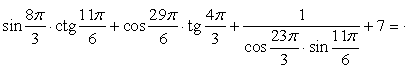
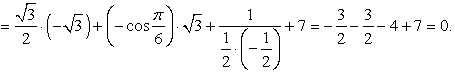 Итак, значение выражения равно 0.Ответ: 0.Комментарий. Для выполнения заданий, связанных с обратными тригонометрическими функциями, нужно, во-первых, четко помнить определения этих понятий:
Итак, значение выражения равно 0.Ответ: 0.Комментарий. Для выполнения заданий, связанных с обратными тригонометрическими функциями, нужно, во-первых, четко помнить определения этих понятий: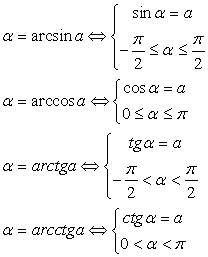 .Удобно при решении таких задач сделать замену (например, α = arcsin x) и работать с более привычным объектом — углом α, лежащем в первой или четвертой четверти тригонометрического круга, синус которого равен х. При этом выясняется, что задача намного проще, чем казалось вначале.Пример 23.Вычислить cos(4arctg 5).РешениеПусть α = arctg5, тогда tg α = 5. Требуется найти cos4α. Вычислим вначале cos2α, используя универсальную подстановку:
.Удобно при решении таких задач сделать замену (например, α = arcsin x) и работать с более привычным объектом — углом α, лежащем в первой или четвертой четверти тригонометрического круга, синус которого равен х. При этом выясняется, что задача намного проще, чем казалось вначале.Пример 23.Вычислить cos(4arctg 5).РешениеПусть α = arctg5, тогда tg α = 5. Требуется найти cos4α. Вычислим вначале cos2α, используя универсальную подстановку: 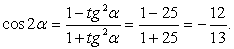 Тогда получаем, что:
Тогда получаем, что: 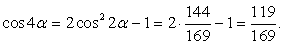 Ответ:
Ответ: 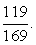 Пример 24.Выразить через все обратные функции
Пример 24.Выразить через все обратные функции 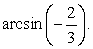 РешениеПусть
РешениеПусть  . Угол α лежит в четвертой четверти, следовательно, cos α >
0.Найдем все тригонометрические функции угла:
. Угол α лежит в четвертой четверти, следовательно, cos α >
0.Найдем все тригонометрические функции угла: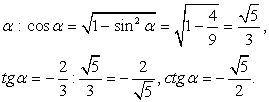 В четвертой четверти находятся арктангенсы отрицательных чисел, поэтому можно утверждать, что
В четвертой четверти находятся арктангенсы отрицательных чисел, поэтому можно утверждать, что 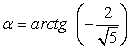 .Но
.Но 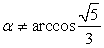 , так как арккосинусы положительных чисел принадлежат первой четверти. В силу четности косинуса cos (-α) = cos α, при этом
, так как арккосинусы положительных чисел принадлежат первой четверти. В силу четности косинуса cos (-α) = cos α, при этом 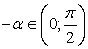 , то есть
, то есть 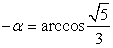 , тогда
, тогда 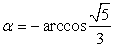 .Арккотангенсы отрицательных чисел расположены во второй четверти. Например,
.Арккотангенсы отрицательных чисел расположены во второй четверти. Например, 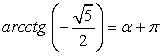 , следовательно,
, следовательно, 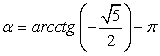 . Таким образом, угол α выражен через все обратные функции.Ответ:
. Таким образом, угол α выражен через все обратные функции.Ответ: 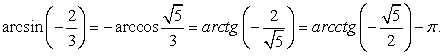 Пример 25Найти arcsin (sin 12).РешениеПо условию задачи требуется найти угол, синус которого равен синусу угла в 12 радиан и который принадлежит промежутку
Пример 25Найти arcsin (sin 12).РешениеПо условию задачи требуется найти угол, синус которого равен синусу угла в 12 радиан и который принадлежит промежутку 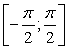 . Заметим, что
. Заметим, что 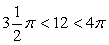 , поэтому
, поэтому 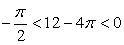 .Поскольку
.Поскольку 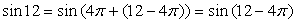 , угол 12º
- 4π является искомым углом: его синус равен sin 12, и он находится в области возможных значений арксинуса.Ответ: arcsin (sin12) = 12º
- 4π.Пример 26.Вычислить
, угол 12º
- 4π является искомым углом: его синус равен sin 12, и он находится в области возможных значений арксинуса.Ответ: arcsin (sin12) = 12º
- 4π.Пример 26.Вычислить 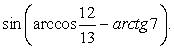 РешениеВведем два угла:
РешениеВведем два угла: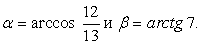 Оба они лежат в первой четверти, значит, все их тригонометрические функции положительны. Мы знаем, что
Оба они лежат в первой четверти, значит, все их тригонометрические функции положительны. Мы знаем, что 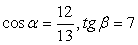 . Требуется найти синус суммы этих углов, а для этого нужно знать их синусы и косинусы.Во-первых,
. Требуется найти синус суммы этих углов, а для этого нужно знать их синусы и косинусы.Во-первых, 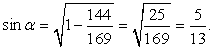 Во-вторых,
Во-вторых, 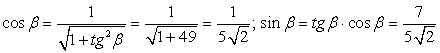 .Следовательно,
.Следовательно, 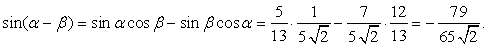 Ответ:
Ответ: 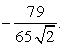
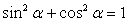 .
.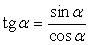 .
.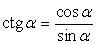 .
.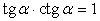 .
.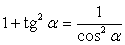 .
.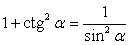 .
.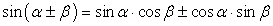 .
.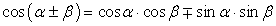 .
.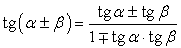 .
.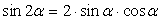 .
.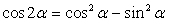 .
.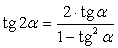 .
.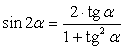 .
.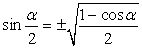 .
.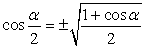 .
.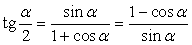 .
.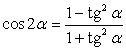 .
.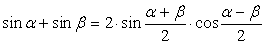
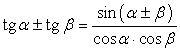
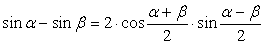
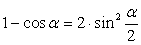
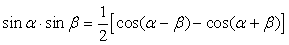 .
.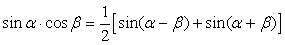 .
.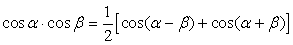 .
.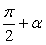
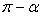
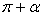
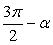
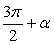
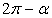
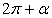
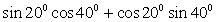 ;
;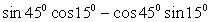 ;
;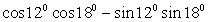 ;
;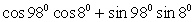 ;
;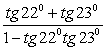 ;
;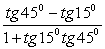 .
.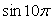 ;
;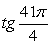 ;
;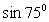 ;
;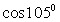 ;
;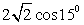 .
.
