Иррациональные числа
 двух отрезков прямой, или двух углов, или двух дуг одинакового радиуса, вообще двух значений одной и той же величины, называется такое значение этой величины, которое в каждом из них содержится целое число раз без остатка. В геометрии же утверждается, что могут быть такие два отрезка, которые не имеют общей меры, например, сторона квадрата и его диагональ. Это отношение может быть выражено только бесконечной непериодической дробью:
двух отрезков прямой, или двух углов, или двух дуг одинакового радиуса, вообще двух значений одной и той же величины, называется такое значение этой величины, которое в каждом из них содержится целое число раз без остатка. В геометрии же утверждается, что могут быть такие два отрезка, которые не имеют общей меры, например, сторона квадрата и его диагональ. Это отношение может быть выражено только бесконечной непериодической дробью: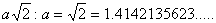 Иррациональные числа. Числа целые, дробные, десятичные конечные и десятичные периодические носят общее название рациональных чисел
Иррациональные числа. Числа целые, дробные, десятичные конечные и десятичные периодические носят общее название рациональных чисел ; десятичные бесконечные дроби непериодические называются иррациональными числами
; десятичные бесконечные дроби непериодические называются иррациональными числами . Первые служат мерою величин, соизмеримых с единицею, вторые — мерою величин, несоизмеримых с единицею.Иррациональное число считается известным
. Первые служат мерою величин, соизмеримых с единицею, вторые — мерою величин, несоизмеримых с единицею.Иррациональное число считается известным (или данным), если указан способ, посредством которого можно находить любое число его десятичных знаков.Два иррациональных числа (как и два рациональных) считаются равными
(или данным), если указан способ, посредством которого можно находить любое число его десятичных знаков.Два иррациональных числа (как и два рациональных) считаются равными , если они произошли от измерения одною и тою же единицею двух равных величин; из двух неравных чисел то считается большим, которое произошло от измерения большей величины. Две равные величины, конечно, должны содержать в себе одинаковое число целых единиц, одинаковое число десятых долей, одинаковое число сотых долей и т.п., поэтому равные иррациональные числа должны быть выражены одинаковыми цифрами. Большая же величина должна содержать в себе большее число целых или — при равенстве целых — большее число десятых, или — при равенстве целых и десятых — большее число, сотых и т.д. Например, число 2,745037... больше числа 2,745029..., так как в первом 6-я цифра выражает число большее, чем 6-я цифра во втором, при тождественности всех предыдущих цифр.Иррациональные числа могут быть положительными и отрицательными, смотря по тому, измеряют ли они величины, считаемые положительными, или величины, считаемые отрицательными.Числа рациональные и иррациональные, положительные и отрицательные получили новое название действительных
, если они произошли от измерения одною и тою же единицею двух равных величин; из двух неравных чисел то считается большим, которое произошло от измерения большей величины. Две равные величины, конечно, должны содержать в себе одинаковое число целых единиц, одинаковое число десятых долей, одинаковое число сотых долей и т.п., поэтому равные иррациональные числа должны быть выражены одинаковыми цифрами. Большая же величина должна содержать в себе большее число целых или — при равенстве целых — большее число десятых, или — при равенстве целых и десятых — большее число, сотых и т.д. Например, число 2,745037... больше числа 2,745029..., так как в первом 6-я цифра выражает число большее, чем 6-я цифра во втором, при тождественности всех предыдущих цифр.Иррациональные числа могут быть положительными и отрицательными, смотря по тому, измеряют ли они величины, считаемые положительными, или величины, считаемые отрицательными.Числа рациональные и иррациональные, положительные и отрицательные получили новое название действительных или вещественных чисел
или вещественных чисел .Приближенные значения иррационального числа. Пусть нам дано какое-нибудь иррациональное число α, т.е. пусть указан способ, посредством которого мы можем получить сколько угодно цифр числа α (этим способом может быть, например, то правило, посредством которого мы находим приближенные квадратные корни с точностью до 1/10 до 1/100 до 1/1000 и т.д.). Положим, мы нашли такие 5 цифр числа α:α = 1,73205080...Возьмем из этих цифр несколько первых, например, цифры 1,73, а остальные отбросим. Тогда мы получим приближенное значение числа α, причем это значение будет с недостатком, так как 1,73<
α. Если последнюю из удержанных нами цифр увеличим на 1, т.е. вместо 1,73 возьмем 1,74, то получим тоже приближенное значение числа α, но с избытком. Обыкновенно из двух приближенных значений, из которых одно с недостатком, другое с избытком, берут значение с недостатком, если первая из отброшенных цифр менее 5, и значение с избытком, если эта цифра больше 5.Сложение иррациональных чисел. Пусть α и β будут какие-нибудь данные положительные иррациональные числа. Если эти числа даны, то это значит, что мы можем найти их приближенные значения с любою точностью. Пусть, например, приближенные значения чисел α и β, взятые с недостатком, будут такие (мы берем приближенные значения
.Приближенные значения иррационального числа. Пусть нам дано какое-нибудь иррациональное число α, т.е. пусть указан способ, посредством которого мы можем получить сколько угодно цифр числа α (этим способом может быть, например, то правило, посредством которого мы находим приближенные квадратные корни с точностью до 1/10 до 1/100 до 1/1000 и т.д.). Положим, мы нашли такие 5 цифр числа α:α = 1,73205080...Возьмем из этих цифр несколько первых, например, цифры 1,73, а остальные отбросим. Тогда мы получим приближенное значение числа α, причем это значение будет с недостатком, так как 1,73<
α. Если последнюю из удержанных нами цифр увеличим на 1, т.е. вместо 1,73 возьмем 1,74, то получим тоже приближенное значение числа α, но с избытком. Обыкновенно из двух приближенных значений, из которых одно с недостатком, другое с избытком, берут значение с недостатком, если первая из отброшенных цифр менее 5, и значение с избытком, если эта цифра больше 5.Сложение иррациональных чисел. Пусть α и β будут какие-нибудь данные положительные иррациональные числа. Если эти числа даны, то это значит, что мы можем найти их приближенные значения с любою точностью. Пусть, например, приближенные значения чисел α и β, взятые с недостатком, будут такие (мы берем приближенные значения 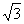 и
и 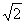 ):
):
до 0,1 |
до 0,01 |
до 0,001 |
до 0,0001 |
|
для числа α ..... |
1,7 |
1,73 |
1,732 |
1,7320 |
для числа β ..... |
1,4 |
1,41 |
1,414 |
1,4142 |
1,7+1,4=3,1,1,73+1,41=3,14,1,732+1,414=3,146,1,7320+1,4142=3,1462;
и меньше каждой из сумм:1,8+1,5=3,3,1,74+1,42=3,16,1,733+1,415= 3,148,1.7321+1,4143=3,1464,
т.е. сложить числа α и β — значит найти такое третье число, которое было бы больше суммы любых приближенных их значении, взятых с недостатком, но меньше суммы любых приближенных значении, взятых с избытком.Взяв приближенные значения чисел α и β, указанные выше, мы можем сказать, что произведение αβ есть число, которое:- больше каждого из произведений: 1,7*1,4=2,381,73*1,41=2,4393,1,732+1,414=2,449048,1,7320+1,4142=2,4493944;
- и меньше каждого из произведений: 1,8+1,5=2,7,1,74+1,42=2,4708,1,733+1,415= 2,452195,1,7321+1,4143=2,464623481129,
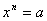 , где a – заданная степень, n – заданный показатель степени, x – неизвестное основание степени.Неизвестное основание x степени находится с помощью действия извлечения корня:
, где a – заданная степень, n – заданный показатель степени, x – неизвестное основание степени.Неизвестное основание x степени находится с помощью действия извлечения корня: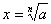 .Корнем n-ой степени из числа a
.Корнем n-ой степени из числа a называется такое число, которое будучи возведено в степень n, дает a.Например,
называется такое число, которое будучи возведено в степень n, дает a.Например, 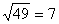 , так как
, так как 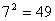 .Положительное значение корня из неотрицательного числа называется арифметическим значением корня
.Положительное значение корня из неотрицательного числа называется арифметическим значением корня .В приведенном примере мы находим арифметический корень. Таким образом, из определения следует, что
.В приведенном примере мы находим арифметический корень. Таким образом, из определения следует, что 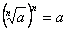 . Это равенство служит для проверки правильности произведенного извлечения корня.Заметим, что
. Это равенство служит для проверки правильности произведенного извлечения корня.Заметим, что 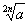 , где n — натуральное число и
, где n — натуральное число и 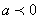 , не существует. Например, выражения
, не существует. Например, выражения 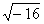 ,
, 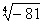 не имеют смысла. Корень нечетной степени извлекается и из отрицательного числа. Например,
не имеют смысла. Корень нечетной степени извлекается и из отрицательного числа. Например, 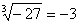 . Чтобы устранить двузначность корня n-ой степени, и ввели понятие арифметического корня.Например,
. Чтобы устранить двузначность корня n-ой степени, и ввели понятие арифметического корня.Например, 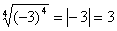 .Пример 1. Определить, при каких значениях x выражения
.Пример 1. Определить, при каких значениях x выражения 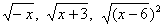 имеют смысл.Решение.
имеют смысл.Решение.- 1) Из определения арифметического квадратного корня следует, что -x≥
0. Умножим обе части этого неравенства на -1 и получим, что
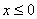 .2) На основании определения арифметического квадратного корня имеем
.2) На основании определения арифметического квадратного корня имеем 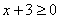 , или
, или 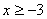 .
.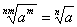 или
или 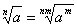 .
.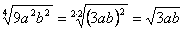 ;
; 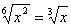 .Величина радикала не изменится, если подкоренное выражение возвысим в какую-нибудь степень и вместе с тем показатель радикала умножим на показатель той степени, в которую возвысили подкоренное выражение.
.Величина радикала не изменится, если подкоренное выражение возвысим в какую-нибудь степень и вместе с тем показатель радикала умножим на показатель той степени, в которую возвысили подкоренное выражение.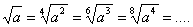
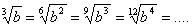
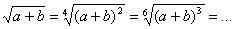 Некоторые преобразования корней
Некоторые преобразования корней- 1) Чтобы извлечь корень из произведения, надо извлечь его из каждого сомножителя отдельно и результат перемножить.
 или
или 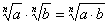 , если
, если 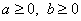 .Например,
.Например, 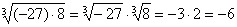 .2) Чтобы извлечь корень из дроби, можно извлечь его из числителя и знаменателя отдельно и первый результат разделить на второй.
.2) Чтобы извлечь корень из дроби, можно извлечь его из числителя и знаменателя отдельно и первый результат разделить на второй.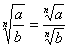 , если
, если 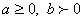 .Например,
.Например, 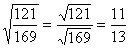 .3) Чтобы возвысить корень в степень, надо возвысить в эту степень подкоренное выражение, оставив тот же показатель корня.
.3) Чтобы возвысить корень в степень, надо возвысить в эту степень подкоренное выражение, оставив тот же показатель корня.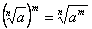 или
или 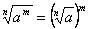 , если
, если 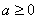 .Например,
.Например, 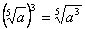 ;
; 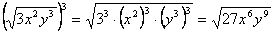 .4) Чтобы извлечь корень из корня, надо перемножить показатели корней.
.4) Чтобы извлечь корень из корня, надо перемножить показатели корней.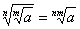 или
или 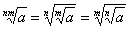 , если
, если 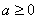 ,
, 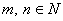 .Например,
.Например, 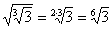 .5) Если подкоренное выражение разлагается на такие множители, что из некоторых можно извлечь точный корень, то какие множители, по извлечении из них корня, могут быть написаны перед знаком корня (т.е. могут быть вынесены за знак корня).
.5) Если подкоренное выражение разлагается на такие множители, что из некоторых можно извлечь точный корень, то какие множители, по извлечении из них корня, могут быть написаны перед знаком корня (т.е. могут быть вынесены за знак корня).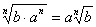 , если
, если 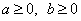 .Например,
.Например, 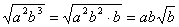 ;
; 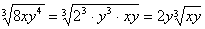 .6) Иногда бывает полезным решить обратную задачу и внести множитель под знак корня. Для этого достаточно возвысить такие множители в степень, показатель которой равен показателю корня, а затем записать множители под знаком корня.Например,
.6) Иногда бывает полезным решить обратную задачу и внести множитель под знак корня. Для этого достаточно возвысить такие множители в степень, показатель которой равен показателю корня, а затем записать множители под знаком корня.Например, 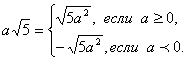 7) Освобождение от иррациональности в знаменателе дроби.
7) Освобождение от иррациональности в знаменателе дроби.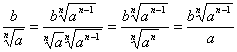 , т.к.
, т.к. 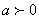 .
.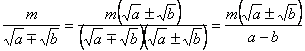 .Например. 1) Исключить иррациональность в знаменателе дроби
.Например. 1) Исключить иррациональность в знаменателе дроби 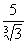 .
.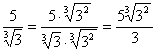 .2) Исключить иррациональность в знаменателе дроби
.2) Исключить иррациональность в знаменателе дроби 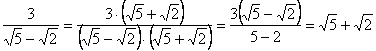 .
.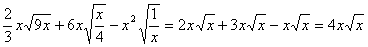 .2)
.2) 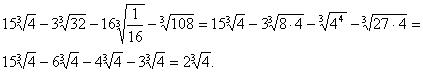 Умножение. Чтобы перемножить несколько радикалов одинаковой степени, достаточно перемножить подкоренные числа. Так:
Умножение. Чтобы перемножить несколько радикалов одинаковой степени, достаточно перемножить подкоренные числа. Так: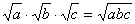 ;
; 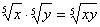 .Если для перемножения даны радикалы c различными показателями, то их можно предварительно привести к одному показателю. Если перед радикалами имеются коэффициенты, то их перемножают.Например: 1)
.Если для перемножения даны радикалы c различными показателями, то их можно предварительно привести к одному показателю. Если перед радикалами имеются коэффициенты, то их перемножают.Например: 1) 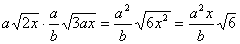 .2)
.2) 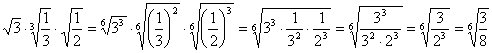 .Деление. Чтобы разделить радикалы с одинаковыми показателями, достаточно разделить их подкоренные числа. Радикалы с различными показателями можно привести предварительно к одинаковым показателям. Если есть коэффициенты, то их делят.Например.
.Деление. Чтобы разделить радикалы с одинаковыми показателями, достаточно разделить их подкоренные числа. Радикалы с различными показателями можно привести предварительно к одинаковым показателям. Если есть коэффициенты, то их делят.Например. 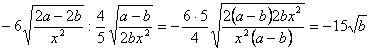 .Возвышение в степень. Чтобы возвысить радикал в степень, достаточно возвысить в эту степень подкоренное число. Так
.Возвышение в степень. Чтобы возвысить радикал в степень, достаточно возвысить в эту степень подкоренное число. Так 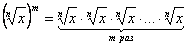 .Например,
.Например, 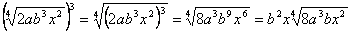 .Извлечение корня. Чтобы извлечь корень из радикала, достаточно перемножить их показатели. Так:
.Извлечение корня. Чтобы извлечь корень из радикала, достаточно перемножить их показатели. Так: 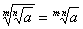 .Например,
.Например, 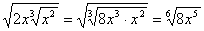 . Видеолекция «Иррациональные числа»:
. Видеолекция «Иррациональные числа»: 
