Рациональные числа
. Количество равных частей, на которые делится единица, называется знаменателем, а количество взятых частей – числителем. Дробь записывается в виде: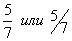
, где 5 — числитель, 7 — знаменатель.Если числитель меньше знаменателя, то дробь меньше 1 и называется правильной дробью.
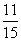— правильная дробь, т.к. 
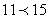.Если числитель равен знаменателю, то дробь равна 1, т.е. 
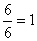.Если числитель больше знаменателя, то дробь больше 1. В обоих последних случаях дробь называется неправильной.
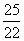- неправильная дробь, т.к. 
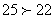.Если числитель делится на знаменатель, то эта дробь равна частному от деления: 
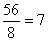. Если деление выполняется с остатком, то эта неправильная дробь может быть представлена смешанным числом: 
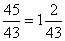. Здесь 1 – неполное частное (целая часть смешанного числа), 2 – остаток (числитель дробной части), 43 – знаменатель дроби.Часто бывает необходимо решать обратную задачу – обратить смешанное число в дробь. Для этого умножаем целую часть смешанного числа на знаменатель и прибавляем числитель дробной части. Это будет числитель обыкновенной дроби, а знаменатель остаётся прежним.Например: представить смешанное число 
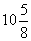в виде дроби.Решение: =
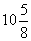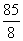.1) 10*8 = 80,2) 80+5 = 85,3)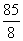.Таким образом, 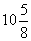= 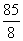.Две дроби называются обратными, если их произведение равно нулю.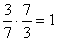
Дробь 
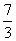- обратная к дроби 
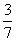.Расширение дроби. Значение дроби не меняется, если умножить её числитель и знаменатель на одно и то же число, отличное от нуля. Это преобразование называется расширением дроби. Например,
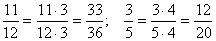.Сокращение дроби. Значение дроби не меняется, если разделить её числитель и знаменатель на одно и то же число, отличное от нуля. Это преобразование называется сокращением дроби. Например,
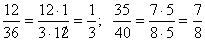.Сравнение дробей. Из двух дробей с одинаковыми числителями та больше, знаменатель которой меньше:
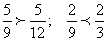.Из двух дробей с одинаковыми знаменателями та больше, числитель которой больше:
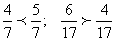.Для сравнения дробей, у которых числители и знаменатели различны, необходимо расширить их, чтобы привести к общему знаменателю.Пример. Сравнить две дроб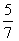и: 
и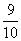 
. Решение: приведем дроби к общему знаменателю, для этого расширим первую дробь на знаменатель второй, а вторую дробь на знаменатель первой и получим:
, 
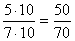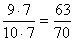.Сравниваем полученные дроби 
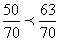и получаем, что 
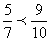.Использованный в этом примере способ приведения к общему множителю через расширение дроби — самый простой и во многих случаях практичный. Единственное его неудобство состоит в том, что общий множитель может оказаться довольно большим, тогда как можно выбрать меньшим. Именно, за общий знаменатель можно взять любое общее кратное (в частности, НОК) данных знаменателей. Тогда нужно расширить каждую дробь на частное, получаемое от деления общего кратного на знаменатель взятой дроби (это частное называется дополнительным множителем).Пример. Даны дроби 
, 
, 
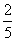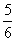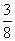. НОК знаменателей 5, 6, 8 равен 120. Определим дополнительные множители: 120:5=24, 120:6=20, 120:5=15. Расширяем первую дробь на 24, вторую на 20 и третью на 15. Получаем:
; 
; 
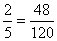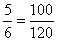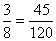.На практике этот способ оправдывается, лишь в том случае, если НОК находится легко подбором. В противном случае приходится затрачивать много времени на отыскание НОК и дополнительных множителей. Кроме того, часто оказывается, что НОК ненамного меньше произведения знаменателей или даже вовсе не меньше его, и тогда затраченное время и труд совершенно бесполезны.Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того, чтобы сложить дроби, надо сложить их числители, а для того, чтобы вычесть дроби, надо вычесть их числители (в том же порядке). Полученная сумма или разность будет числителем результата; знаменатель останется тем же. Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел мы рекомендуем сначала преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа.Пример 1. 
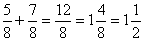.Пример 2. 
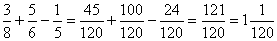.Если складываются смешанные числа, то отдельно находят сумму целых и сумму дробных частей.Пример 3. 
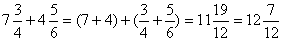.При вычитании смешанных чисел дробная часть вычитаемого может оказаться больше дробной части уменьшаемого, тогда в уменьшаемом «занимается» единица и обращается в неправильную дробь.Пример 4. 
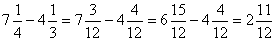.Пример 5. 
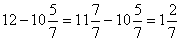.Умножение дробей. Умножить некоторое число (целое или дробное) на дробь означает разделить это число на знаменатель дроби и результат умножить на числитель. Следовательно, мы имеем общее правило умножения дробей: чтобы умножить дробь на дробь, умножают числительна числитель и знаменатель на знаменатель. Первый результат есть числитель, второй – его знаменатель.Если среди сомножителей есть смешанные числа, то их предварительно обращают в неправильную дробь. Еще до перемножения можно сократить любой множитель числителя с любым множителем знаменателя на общий множитель.Пример 1. 
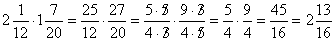.Все сказанное распространяется на случай, когда сомножителей больше двух.Пример 2. 
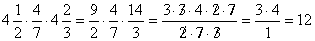.Если среди сомножителей есть целые числа, то каждое из последних можно рассматривать как дробь со знаменателем 1.Пример 3. 
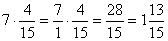.Деление дробей. Определение деления данное в разделе «Натуральные числа», сохраняется и для деления дробей. Чтобы разделить какое-нибудь число на дробь, нужно умножить это число на дробь, обратную делителю.Пример 1. Выполнить действия: 
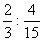.Дробь, обратная 
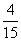, есть дробь 
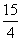. Следовательно, 
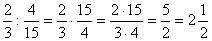.Это правило применимо и в том случае, когда делимое и делитель – целые числа.Пример 2. 2:5 = 
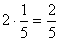.Поэтому дробная черта равносильна знаку деления.Действия с нулем- Сложение. Прибавление нуля к некоторому числу оставляет последнее неизменным:
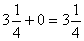; 4+0 = 4. - Вычитание. Вычитание нуля из какого-либо числа оставляет последнее неизменным:
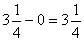; 4-0 = 4. - Умножение. Произведение нуля на любое число равно нулю:
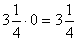; 4*0 = 0; 0*0 = 0. - Деление. Частное от деления нуля на какое-либо число, отличное от нуля, равно нулю: 0:4=0; 0:
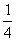=0.
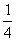, ибо 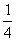*0=0. Можно сказать, что задача деления нуля на нуль имеет бесконечное множество решений, и без указания дополнительных данных действие 0:0 не имеет смысла. Дополнительные данные должны стоять в указании того, каким образом изменялись величины делимого и делителя до того, как они стали нулями. Если это известно, то в большинстве случаев можно выражению 0:0 придать смысл. Так, если известно, что делимое принимало последовательно значения 
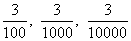и т.д., а делитель 
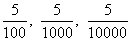и т.д., то частное в это время было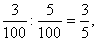 
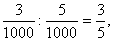
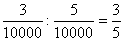и т.д., т.е. оставалось равным 
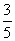, поэтому и частное 0:0 считается равным 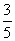. В таких случаях говорят о «раскрытии неопределенности».Частное от деления какого-либо числа, отличного от нуля, на нуль не существует, так как в этом случае никакое число не может удовлетворять определению частного. Однако число, близкое к нулю, можно разделить на число, как угодно близкое к нулю, и чем ближе делитель к нулю, тем больше будет частное. Так, если будем делить 7 на 
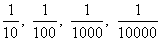и т.д., то получим частные 70, 700, 7000, 70000 и т.д., которые неограниченно возрастают. Поэтому говорят, что частное отделения 7 на 0 «бесконечно велико» или равно «бесконечности», и пишут 7:0=
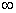. Смысл этого выражения состоит в том, что если делитель приближается к нулю, а делимое остается равным 7 (или приближается к 7), то частное неограниченно увеличивается.Целое и частьНахождение части по целому. Чтобы найти некоторую часть числа, умножают его на дробь, выражающую эту часть.Пример 1. Найти 
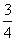от числа 520.Решение: 
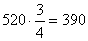.Нахождение целого по части. Чтобы найти число по величине данной его части, делят эту величину на дробь, выражающую данную часть.Пример 2. Найти число, если его 
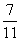равно 63.Решение: 
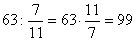.Выражение части в долях целого. Чтобы выразить часть в долях целого, часть делят на целое.Пример 3. Какую часть от числа 45 оставляет число 27?Решение: 
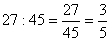.Десятичная дробь есть результат деления единицы на десять, сто, тысячу и т.д. частей. Эти дроби очень удобны для вычислений, так как они основаны на той же позиционной системе, на которой построены счёт и запись целых чисел. Благодаря этому запись и правила действий с десятичными дробями фактически те же, что и для целых чисел. При записи десятичных дробей нет необходимости отмечать знаменатель, это определяется местом, которое занимает соответствующая цифра. Сначала пишется целая часть числа, затем справа ставится десятичная точка. Первая цифра после десятичной точки означает число десятых, вторая – число сотых, третья – число тысячных и т.д. Цифры, расположенные после десятичной точки, называются десятичными знаками.Пример: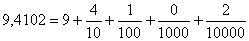 
.Одно из преимуществ десятичных дробей – они легко приводятся к виду обыкновенных: число после десятичной точки (в нашем случае 4102) – это числитель; знаменатель же равен n–ой степени 10, где n - количество десятичных знаков (в нашем случае n=4):
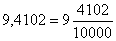.Если десятичная дробь не содержит целой части, то перед десятичной точкой ставится ноль:
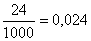.Свойства десятичных дробей- Десятичная дробь не меняется, если справа добавить нули:12,7=12,70=12,700=12,7000 и т.д.
- Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби:0,00830=0,0083.Внимание! Нельзя удалять нули, расположенные не в конце десятичной дроби!
- Десятичная дробь возрастает в 10, 100, 1000 и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо:13,058
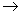1305,8 (число увеличилось в 100 раз). - Десятичная дробь уменьшается в 10, 100, 1000 и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево:176,24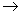17,624 (уменьшилось в 10 раз);176,24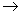0,17624 (уменьшилось в 1000 раз).
. Период записывается в скобках. Например, 0.12345123451234512345… = 0.(12345).Пример. Если разделить 10 на 3, то получим 3,33333333333… = 3.(3).Сложение и вычитание десятичных дробей. Эти операции выполняются так же, как и сложение и вычитание целых чисел. Необходимо только записать соответствующие десятичные знаки один под другим, учитывая разрядность.Пример.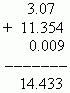 
. Умножение десятичных дробей. На первом этапе перемножаем десятичные дроби как целые числа, не принимая во внимание десятичную точку. Затем применяется следующее правило: количество десятичных знаков в произведении равно сумме десятичных знаков во всех сомножителях.Замечание: до простановки десятичной точки в произведении нельзя отбрасывать нули в конце!Пример. 
.Сумма чисел десятичных знаков в сомножителях равна: 3+4=7. Сумма цифр в произведении равна 6. Поэтому необходимо добавить один ноль слева: 0197056 и проставить перед ним десятичную точку: 0.0197056.Деление десятичных дробейДеление десятичной дроби на целое число. Если делимое меньше делителя, записываем ноль в целой части частного и ставим после него десятичную точку. Затем, не принимая во внимание десятичную точку делимого, присоединяем к его целой части следующую цифру дробной части и опять сравниваем полученную целую часть делимого с делителем. Если новое число опять меньше делителя, ставим ещё один ноль после десятичной точки в частном и присоединяем к целой части делимого следующую цифру его дробной части. Этот процесс повторяем до тех пор, пока полученное делимое не станет больше делителя. После этого деление выполняется, как для целых чисел. Если делимое больше делителя или равно ему, сначала делим его целую часть, записываем результат деления в частном и ставим десятичную точку. После этого деление продолжается, как в случае целых чисел.Пример 1. Разделить 13,28 на 64. 13,28:64=0,2075.Для того, чтобы обратить обыкновенную дробь в десятичную, надо разделить числитель на знаменатель в соответствии с правилами деления.Пример 2 . Обратить в десятичную дробь.Решение. Делим 5 на 8, получаем 0,625.В большинстве случаев этот процесс может продолжаться бесконечно. Тогда невозможно точно обратить обыкновенную дробь в десятичную. Но на практике это никогда и не требуется. Деление прерывается, если представляющие интерес десятичные знаки уже получены.Пример 3. Обратить 1/3 в десятичную дробь.Решение. Деление 1 на 3 будет бесконечным: 1:3 = 0.3333…Деление одной десятичной дроби на другую. Сначала переносим десятичные точки в делимом и делителе на число десятичных знаков в делителе, то есть делаем делитель целым числом. Теперь выполняем деление, как в предыдущем случае.Пример 4. Разделить 0.04569 на 0.0006.Решение. Переносим десятичные точки на 4 позиции вправо и делим 456.9 на 6: Видеолекция «Рациональные числа»: 
